基于蚁群优化的多目标资源配置模型及应用

喻江平

(燕山大学经济管理学院，河北秦皇岛 0660044)

基于蚁群优化的多目标资源配置模型及应用

喻江平

(燕山大学经济管理学院，河北秦皇岛 0660044)

多目标资源配置问题就是将有限资源分配到不同事件来获得预期目标。为满足未来的特定要求，一般需同时对多个目标(如成本最小化或效率最大化)进行优化。为有效获取一组帕累托解，提出一种改进蚁群算法，该方法可通过增加蚂蚁的学习来提高求解效率。通过比较蚁群算法和混合遗传算法所得的实验结果，验证了改进蚁群算法的可行性、有效性及正确性。

蚁群优化；多目标优化；资源配置

0 引言

20世纪60年代早期，多目标优化问题开始受到各领域研究者越来越多的关注。在多目标优化问题中，需同时优化多个目标。在多目标情况下，由于不同目标之间会相互冲突；对于所有目标而言，不一定存在一个最优解。一个目标中的最优解可能在另一个目标中却是最劣解。在多目标情形下，通常存在一组彼此之间不能作简单比较的问题解。这类解被称为帕累托最优解，即除非至少牺牲一个其他目标函数，否则无法对任何函数进行改进。

针对多目标资源配置问题，本文基于蚁群算法提出了一种新的求解方法。为确保资源约束得以满足，还提出了使用自适应资源界限。实验结果证明这种基于蚁群算法的方法比遗传算法更适合求解模拟多目标资源优化问题。

1 多目标资源配置问题

本文主要研究多目标人力资源配置问题的多阶段决策模型。在不失一般性的情况下，优化是指在可能选择上寻求问题解以优化某准则。

⑴符号及参数定义：

i：表示任务指标，i=1,2,…,N;

j：表示员工数量，j=0,1,2,…,M;

N：表示任务总数；

M：表示员工总数；

cij：表示分配到j个员工时任务i的成本；

eij：表示分配到j个员工时任务i的效益；

⑵决策变量：

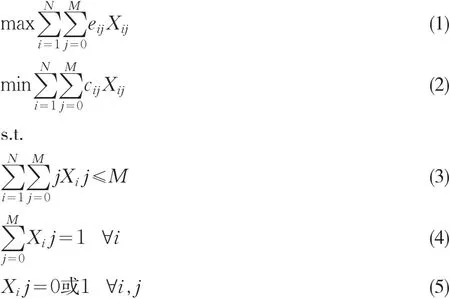
目标函数(1)表示将所有任务的总效益最大化；目标函数(2)表示将所有员工的总成本最小化；约束(3)确保所分配员工的数量不超过员工总数量；约束(4)确保各个任务i只能获得一次员工分配。帕累托最优解通常是多目标规划问题的解。因此，在实施蚁群算法时，增加一个模块来处理帕累托最优解。

2 求解多目标资源配置问题的蚁群优化算法

蚁群优化算法最早是由Dorigo提出并鼓励其他学者开发处理NP-hard问题，如旅行商问题、二次分配问题、调度问题、最小权顶点覆盖问题和曲线分割问题等。蚁群算法受到了对真实蚂蚁觅食行为研究的启发。研究者观察到蚂蚁可以利用信息素构建从蚁巢到食物源之间的最短路径。

蚁群算法模仿真实蚂蚁的觅食行为，这些蚂蚁通过沿路分泌信息素的方式进行食物源的信息交流，当有蚂蚁找到食物源后它便会返回蚁巢。由于较短路径上的蚂蚁将较快返回蚁巢，因此，这些路径将聚集更多的信息素。行进中的蚂蚁将根据信息素数量按照某概率进行路径选择，所以越多蚂蚁经过的路径则对其他蚂蚁的吸引力越大，此外通过自我加强行为，会有更多蚂蚁经过这些路径。而且，信息素经过多次挥发，会使那些蚂蚁经过次数较少的路径上的信息素浓度变弱，而那些吸引力大的路径上的信息素浓度则变强。人工蚂蚁不仅模仿以上所述的学习行为，还会经常应用另外一些特定问题的启发信息。当这种人工蚁群系统已成功应用于各种单一目标问题之后，为了能够求解多目标问题，需要对其进行一些扩展。

2.1 解的构造

将多目标资源配置问题的可行解看作是资源分配置换，将解的各个部分称为状态。分配数量j的资源给第i个项目被称为一个移步，表示为V(i,j)；移步Vk将蚂蚁k从状态S1移动到状态S2，从而逐渐使局部解完整。一旦数量j的资源被分配到蚂蚁k的解中第i个项目时，则必须根据新的资源数量对可利用资源数量进行更新，且所有不可行移步资源必须保存到禁忌表中，表示为Tabuk。该禁忌表是蚂蚁k用来保存不可行分配指标的内存。除了表Tabuk，蚂蚁k选出的所有移步都保存在内存中，表示为Vk。蚂蚁k从当前状态移动到下一个状态，利用表Tabuk来避免所需资源已利用完的项目的分配问题。内存Vk在迭代最后被用来更新蚂蚁所选出的移步的信息素。假设按照升序顺序预定资源分配，也就是说，每只蚂蚁首先将资源分配给项目1，然后分配给项目2，以此类推，直到获得完整解。在每次分配中，会将不可行分配增加到那只蚂蚁的禁忌表中。因此，约束方程式(3)-(5)得到满足。这使得每只蚂蚁都能产生可行解。

2.2 启发信息

不同于真实蚂蚁的盲目，人工蚂蚁在不同项目中进行资源分配时，可以获取一些启发信息。适合移步V(i,j)的启发信息表示为ηij。这种信息表示将数量j的资源分配给项目i的期望值，可采用启发式方法进行计算。每个移步期望值都有几种评估方法。由于所有蚂蚁中的所有移步都要计算启发信息，这样可能会使算法效率极大地降低，因此应当提高计算效率。可以在蚂蚁算法中考虑该要素的复杂性。从开始构造解到结束构造，在不考虑可行性问题的情况下，每只蚂蚁都有可能将数量M的资源分配给所有项目，所以每只蚂蚁在算法的每次迭代中应总共计算启发信息M×N次。因此，对于整个算法而言，该要素的复杂性变成O(I×A×M×N)，其中，I表示迭代次数，A表示每次迭代的蚂蚁数量。在较早实施蚂蚁算法时，计算得出的启发信息要么是先验信息，要么是后验信息。在实施第一种启发信息时，首先计算启发信息，剩下的在算法运行过程中保持不变；在实施第二种启发信息时，该信息是动态的，主要由蚂蚁的当前状态决定。在计算启发信息时，考虑这两个方面，一个是计算效率；另一个是信息质量。先验启发信息的实施效率较高，但不能完全反映移步的期望值。相反地，在第二种实施方式中，虽然计算效率不令人满意，但却能获得各个移步期望值的精确评估。本文试图结合这些原理以开发出启发信息的有效计算方法。这种方法选择对第二种启发信息进行计算，即后验信息。但是，与其它一些类似方法相比，该方法的计算复杂性相对较低。这种公式考虑各个移步对目标函数值的局部贡献量。p表示构建下的分配置换。由于要计算项目置换移步V(l,j)的期望值直到1，即p(1),p(2),…,p(l)已知，因此，可对移步V(l,j)的局部贡献量进行以下计算：

移步V(l,j)对第一个目标函数的局部贡献量为：

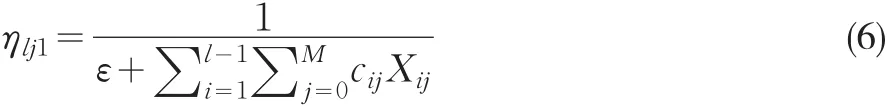
式中，ε表示小的正数，原因是在式(6)的分母中增加ε可以避免除0。移步V(l,j)对第二个目标函数的局部贡献量为：

在O(L×N)中可获得方程式(6)和(7)给定的启发信息。可以采取多种方式结合多目标问题中的期望值以得到各个移步的总期望值，文中提出以下公式对V(l,j)的总期望值进行计算：

2.3 信息素更新规则

蚁群算法是依靠蚂蚁个体间的相互协作。在每次迭代中，通过迭代地应用节点转移规则，每只蚂蚁从一个阶段移动到下一个阶段，直到进入汇聚节点并在此构建问题的候选解。在进行下一个迭代之前，根据信息素更新规则对各边信息素数量进行更新，再根据求解单一目标函数问题中的原始蚁群算法，按照方程式(9)来更新各边信息素数量：

其中，ρ∈(0 ,1)表示信息素的挥发率；τij(t)表示边ij上信息素更新后的数量，即数量为j的资源分配给任务i；τij(t -1)表示这条边上之后的信息素数量；Δτ(t -1)表示当前迭代过程中蚂蚁在边ij上所释放的信息素数量。显然，若蚂蚁在当前迭代过程中没有遍历边ij，则Δτ(t -1)=0。否则，须对Δτ(t -1)进行计算。现实世界中，绝大多数蚂蚁会在经过的每条边上释放固定数量的信息素，但人工蚂蚁所释放的信息素则与所构造解的质量有关，在求解单一目标函数问题的原始蚁群算法中，采用以下公式计算Δτ(t -1)

其中，Xt表示蚂蚁所构建的候选解。本文提出了另一种更加有效的计算方法。根据不可能存在一个所有目标函数的最优解这一事实，将所有帕累托解看作是多目标函数问题的最优解。假设所有非支配解具有相同、最好的质量，且忽略所有支配解，则可根据以下规则计算Δτ(t +1)

其中，δ表示小的正数，t表示当前迭代次数。式中，比较当前迭代中所构建的各个解与之前所有的非支配解，如果是非支配解，则所有边上的信息素数量将增加t×δ。t乘以δ的原因是通过增加对应t的可行解集，发现非支配解更接近第一级（或最好的）非支配水平。在第N次迭代中的一些非支配解会受到第N+1次迭代中的一些解的支配。这条规则主要尝试增加蚂蚁的学习。

2.4 选择概率

在蚂蚁算法的所有实施过程中，通过结合两个因素，即移步的期望值和所遍历边上的信息素数量，一只蚂蚁可以选择从当前状态S1移动到下一个相邻状态S2。本文基于文献所提出方法，在进行修改后，采用其对选择概率进行计算。这里，采用并修改该方法的主要原因有两个，一个是该方法只有一个控制参数α，用来映射信息素数量与各个移步期望值的相对重要性，比较简单，而其它方法则每个因素需考虑一个参数；另一个原因是由于采用乘法而非求幂运算，该方法的计算效率较高。以下我们会解释该方法的具体产生过程。根据文献所提出的方法，蚂蚁k按照以下概率选择遍历边ij

应该方程式(11)可能会导致某个移步出现负概率。我们研究了两种策略在处理负概率移步时所表现出来的性能。避免了负概率移步，只在正概率移步中进行选择。如果没有正概率移步，那么以同等机会选择移步。在其它移步概率中增加最负的概率的绝对值，然后根据累计概率进行新概率的计算，从而使得所有概率都变成正概率。值得注意的是第一种策略中的搜索空间比第二种策略中的搜索空间更小。这与我们的实验观察相符，表明第二种策略比第一种策略更好。本文所提出方法的执行过程是：在应用方程式(12)对各个资源分配的概率进行计算之后，如果出现任何负概率，则采用第二种策略。

3 实例运算及其结果

3.1 数据来源及算法步骤

为了验证本文方法的可行性及有效性，笔者采用国际上通用的测试实例来进行实例验证工作。本文采用国际上通用的测试实例来验证本文方法的可行性及有效性。该测试实例来自于参考文献[3]，该实例主要是将10个员工分配给4个任务。本文章主要采用混合遗传算法和蚁群优化算法来求解该问题。

蚁群优化算法的主要步骤如下：

初始化

⑴设置ρ、d、a和t0的参数值；A表示蚂蚁数量；Max_Iter表示最大迭代次数

⑵初始化所有边的信息素数量

⑶对于k=1到A

⑷对于i=1到任务

①选取所有不可能移步

②计算所有目标函数的所有可能移步

③按照第二种策略，计算所有可能移步的概率

④进行分配

⑤更新可利用资源

评估

⑸计算对应构造解的目标函数

⑹比较构造解与蚂蚁k的其它解，确定其是否为帕累托解或非支配解

信息素更新

⑺比较所有蚂蚁全部已标注“非支配”字样的解，并选择最终的非支配解

⑻更新信息素数量。

⑼若总迭代次数少于Max_Iter，则转至步骤3，否则停止结束

3.2 实例运算结果

本文提出的蚂蚁算法在Borland Delphi 7中加码，采用型号1.8 GHz Centrino的计算机执行操作。该方法包含五个参数，A、ρ、α、d和t0。这些参数会对算法的性能产生影响。通过大量实验研究，可以看出不同参数值对该蚂蚁算法性能的影响。根据观察，提出了以下实验推导规则来设置参数值。

A=5×M，最大迭代次数(max_iteration)=N，α=0.5，δ=0.05/N，t0=0.01，ρ=0.3

表1和表2分别表示期望效率和期望成本。下面的表3和表4则分别采用混合遗传算法和本文所提出的蚁群算法对帕累托解进行求解。实验结果表明，本文所提出的蚁群算法比混合遗传算法更适合求解多目标资源分配问题。

表1 期望成本Cij

表2 期望效率Eij

表3 采用混合遗传算法求得的帕累托解

表4 采用蚁群优化算法求得的帕累托解

4 结束语

多目标资源配置问题就是将有限资源分配到不同事件来获得预期目标。资源是指有限供应的人力、资产、原材料或其它任何可以完成目标的事物。资源配置问题的应用十分广泛，包括产品分配、资源配置、项目预算、软件测试、卫生资源配置等。

(1)提出了求解多目标资源配置问题的改进蚁群优化算法，该算法通过增加蚂蚁在更新信息素规则中的学习和简化概率计算来提高算法效率和有效性。

(2)在相同问题中比较了混合遗传算法与该蚁群优化算法的求解结果，实验结果表明蚁群算法会产生一半非支配解，其绩效优于混合遗传算法。

[1]CM Fonseca,PJ Fleming.An Overview of Evolutionary Algorithms in Multi-objective Optimization[J].Evolutionary Computation，1995，3(1).

[2]YC Hou,YH Chang.A New Efficient Encoding Mode of Genetic Algo⁃rithms for the Generalized Plant Allocation Problem[J].Journal of In⁃formation Science and Engineering,2004,20.

[3]Chi-Ming Lin,Mitsuo Gen.Multi-objective Resource Allocation Problem by Multistage Decision-based Hybrid Genetic Algorithm[J].Applied Mathematics and Computation,2007,187.

[4]M Dorigo.Optimization,learning,Natural Algorithms,Ph.D.Thesis,Dip.Elettronica e Informazione,Politecnico di Milano[Z].Italy,1992.

[5]Kalyanmoy Deb.Multi-Objective Genetic Algorithms:Problem Diffi⁃culties and Construction of Test Problems[R].Technical Report CI-49/98,Dortmund:Department of Computer Science/LS11,University of Dortmund,Germany,1998.

[6]DE Goldberg,J Richardson.Genetic Algorithms with Sharing for Mul⁃timodal Function Optimization[C].in:Proceedings of the First Interna⁃tional Conference on Genetic Algorithms and Their Applications,1987,(41).

F224

A

1002-6487（2013）14-0082-04

喻江平（1979-），男，湖南宁乡人，硕士研究生，讲师，研究方向：宏观经济学。

（责任编辑/易永生）