农产品价格波动时的数理微分模型分析

夏凡捷，夏新念

（1.武汉大学 经济与管理学院，武汉 430072；2.武汉工程大学 机电工程学院，武汉 430074）

农产品价格波动时的数理微分模型分析

夏凡捷1，夏新念2

（1.武汉大学 经济与管理学院，武汉 430072；2.武汉工程大学 机电工程学院，武汉 430074）

价格理论是微观经济学的核心，供求关系是经济学研究的起点。长期以来，人们对价格形成机制以定性的探讨为主，较少或缺乏定量的分析研究。文章尝试运用数理分析方法，以典型农产品价格波动为例，探讨在完全竞争条件下均衡价格的市场实现机制。文中不仅发现了采用标准二阶微分模型最能恰当描述农产品在竞争条件下的价格波动过程，而且还揭示了决定二阶微分模型参数的信息其实还隐藏在供求关系之中。

均衡价格；供求弹性；动态经济学；数理微分模型；蛛网模型；价格变动加速度

0 引言

市场是商品交换的场所，也是商品的生产者之间、商品生产者与商品消费者之间竞争的场所。竞争的结果导致商品的供给、需求的变化，进而影响到商品价格的变化。商品的供求及价格决定，即市场中的均衡分析是经济分析中的最基本的问题之一。其中价格理论是微观经济学的核心，供求关系是经济学研究的起点。长期以来，对价格形成机制的探讨一直是经济学关注的重点问题之一，但常常是以静态或比较静态的方式研究该问题，缺乏动态和定量的考察。在国外，现代经济学大量运用动态分析来考察有关的经济问题[1]，发展出一门称作动态经济学（或经济动力学）的学科。本文试图从完全竞争市场出发，以典型农产品为例，借荐物理学分析方法，建立均衡价格（或均衡产量）的数理微分动态模型。

静态均衡分析是在假定市场已处于均衡状态的情况下，分析经济变量达到均衡的条件，并考察均衡状态的特性及其影响因素，这时不用考虑时间的影响。在均衡分析过程中，假定商品数量对价格的变化能够得到即时的反应。也就是说商品价格的变化会立即作用于商品的供给和需求，并同时引起供给量和需求量的变化。

但在现实生活中，市场诸因数往往是随时间而变的，当价格变化后，许多商品的需求量和供给量对价格变化的反应在时间上并不一致。一般来说，需求量对价格的反应是即期的，可以用即时反应来表示，而供给量对价格的反应往往有一个滞后期，尤其对于农产品类商品更为典型。如果能动态地研究均衡价格的实现过程就是一项很有意义的工作，为达到该目的，此时若借用物理学中动力学分析方法（或经济学中被称之为动态分析的方法），就能达到事半功倍的效果。

1 蛛网模型

蛛网模型是动态模型中出现得较早的一种模型，它虽是一种图解模型，但由于具有形象直观、便于分析等优点，长期以来一直用于价格形成机制的定性说明中。一般用作对生产周期较长的商品（如农产品、畜产品）的价格和产量的观察、预测。

蛛网模型的假定条件[2]是：（1）生产者开始生产某种产品到该种产品上市需要一定的时间，市场信息极不灵通，生产者对其产品的预期价格和预期需求一无所知，只好以上期的价格作为本期供给量的依据QS(t)=QS(Pt-1)，但产品需求量却可以随市场价格做即期变动Qd(t)=Qd(Pt)；（2）产品均为不耐贮藏的商品，为了减少损失，需要在当期（年）清空市场，即Qd(t)=QS(t)；3）市场成交价格取决于在给定的供给量QS(t)下消费者愿意支付的价格，即成交价格Pd(t)=Pd(QSt)。

在上述假定下，只要供给和需求满足一定的条件，是可以自动实现价格均衡的。现以一个西瓜市场（或生猪市场）以一年为周期的价格波动中自动趋向市场均衡的示例来做说明[3]。假设西瓜供给函数为：QS(t)=-0.5+8p(t-1)，西瓜的需求函数为：Qd(t)=7.0-12 p(t)。西瓜不易保存，为了减少损失，当年生产的西瓜必需当年销售完毕，即：QS(t)=Qd(t)。如果供给过多，市场价格必然下降；如果供给不足，市场价格自然上升。市场价格完全取决于消费者愿意支付的价格。于是价格会往复波动起来。假设初期西瓜的价格是0.8元/千克，运用蛛网模型可画出价格蛛网图。如图1所示。

图1 市场价格波动的蛛网模型

从图中可看出，市场价格最后将趋于均衡价格。

2 一阶差分模型

由于蛛网模型的定性意义大于定量作用，如果要想较好地使用数学，上述过程实际上可通过差分方法表示出来。若上年（2000年）西瓜价格是0.8元/千克，则当年（2001年）的价格是：7.0-12p(2001)=-0.5+8×p(2000)=-0.5+8×0.8 ，得：p（2001）=0.09166元/千克。依次类推，依据p(t+1)=7.5+p(t)2/3，可逐年算出西瓜其它年的价格：

由此可见，西瓜价格逐年变动，但总是围绕均衡价格p*=0.375（元/千克）上下波动，并逐渐趋于均衡价格。

蛛网模型是一种图解模型，能够说明价格变动的趋势，并判断均衡价格。但模型相当粗糙，难以看出时间在其中的具体作用过程。不管是蛛网模型，还是一阶差分模型，连续的时间在模型中都是离散的。价格在一年中只能取一个值，但这个值是平均值、最终值？还是最大值、加权平均值？难以辨别。蛛网模型只能看作是动态模型的初级近似。

3 一阶微分模型

为了克服上述模型的不足，可将价格看作是随时间连续变化的函数。假设在需求、供给曲线都不变的条件下，再来考察价格随时间的变化过程。

已知需求函数为：Qd(t)=bd-adp(t)，ad＞0；供给函数为：QS(t)=-bs+asp(t)，aS＞0。并假定某一个时刻由于某种原因价格未能处在均衡价格位置。由瓦尔拉斯稳定性判定条件知[4]，如果存在超额需求，即E(pt)=Qd(t)-QS(t)并是正的，买主倾向于提高他们的出价；如果存在超额供给，即超额需求E(pt)=Qd(t)-QS(t)并是负的，则卖主倾向于降低他们的价格。于是有理由相信，超额需求（或超额供给）的存在是引起价格变动的主要原因。即价格变动量与超额需求成正比，据此可假设有一阶微分方程成立：

从数学角度看，这是一阶线性常微分方程式，它的通解是：p=Ce-(ad+as)t/μ+p*。其中：p*=(bd+bs)/(ad+as)。考虑初始条件，当t=0时，p=p0。故C=p0-p*。则一阶微分模型的最终解为：p=(p0-p*)e-(ad+as)t/μ+p*。当t→∞时，p→p*。该模型也说明了经过一定的时间后，产品价格将趋于均衡价格。

图2 一阶模型价格变动趋势

一阶微分模型虽是数学解析模型，可以对价格进行分析和计算，也能判断价格的走势。但从图2看，它并没有即时反映价格在均衡价格上下随时间波动的情况，这说明它还只是反映了价格变动规律的一个侧面。因此它应属于一个不完全的动态模型。

4 二阶微分模型辨析

一阶微分模型认为，超额需求（或超额供给）的存在是影响价格变动的主要原因。表面上看，此观点不错，但若仔细思考起来，却似乎没有这么简单。回想物理学在伽利略及以前时代，人们对力的认识，虽已有所了解，但仍很模糊。对力是如何影响运动的以及是不是引起物体运动的直接原因还认识不清。自从亚里士多德时代以来，人们就曾朴素地认为，重力是致使物体下落（位置变化）的直接原因，并且凭直觉直观地认为越重的物体下落越快。直到伽利略做出传说中的比萨斜塔实验，并在“关于两门新科学的对话”等名篇中说明了两个不同重量（但同体积）的物体下落也能一样快，通过实证推翻了近两千年存在于人们头脑中的不正确的东西。并将运动区分出速度与加速度的不同，并首次提出了加速度的概念。在这个实验的基础上，才由天才的牛顿总结出牛顿定律，说明力是产生运动变化的原因，而不是直接对运动（位置变化）发生影响。

伽利略自由落体实验给我们对经济学的研究带来这样启示：它说明重力在一般情况下虽然导致物体的下落（位置变化），但重力不是引起物体位置变化的直接原因，重力不与速度成正比，重力直接影响的实际上是加速度（速度的变化率）大小。若物体有加速度，则物体速度必然变化，物体最终位置当然相应发生变化。有重力，就有加速度，这是现代物理学常识，但正是这一点在当时还经历了一个相当漫长的认识过程。

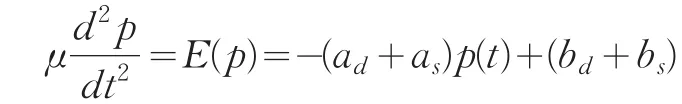
此解显示出，价格将作无休止的波动，并不收敛于均衡价格。与一阶模型相比较，一阶模型只收敛，不波动；此处二阶模型只波动，不收敛。看来它们都未完全准确反映价格既波动又收敛的实际情况。

5 有阻尼二阶微分模型建立

上述二阶模型为什么不收敛于均衡价格，就在于该模型只考虑影响价格波动的弹性因素，未考虑影响价格波动的阻尼因素。而在蛛网模型中，阻尼因素是隐含存在于图形之中的，故价格才能收敛于均衡价格。但蛛网模型只能给出了图解结果。我们知道，在蛛网模型的讨论中，并不是任意的供求弹性都能使价格自动调节到均衡价格，在总共三种变化情形中其实只有一种情形才是收敛的，即是要求需求曲线的斜率ad大于供给曲线的斜率aS。否则就不收敛于均衡价格。

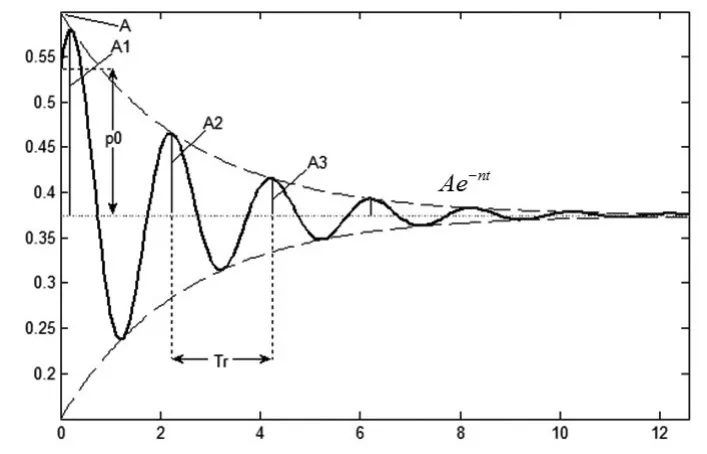
图3 价格波动随时间变化关系

从图3可以形象看出价格随时间的瞬时变化关系，并围绕均衡价格 p*上下波动。波幅Aj=Ae-nTr是随着时间的延长而越来越小的，最后趋于零。这说明这种二阶模型比较好地反映了价格系统的动态均衡。在现实生活中，完全竞争的农产品市场与上述模型较为接近。可以用上述模型解释农产品价格波动规律。

6 二阶微分模型参数的统计推断

余下的问题是，假若有某种方法能够确定二阶模型中的参数n和ω或c和μ，那么描述价格波动的微分方程就完全决定了下来。此时解决问题的办法是：如果价格波动的周期能为某种统计学数据统计推断出来，上述问题就迎刃而解。

7 阻尼系数与供求弹性的关系分析

但是，上述计算二阶模型参数的方法尚存在不足，它需借助于蛛网模型或需单独计算两个时期的Aj和Aj+1，然后才能计算出ln(Aj/Aj+1)。能不能直接预测出这些参数的数值呢？

因此，Aj/Aj+1=(ad/aS)2，则 n=ln(Aj/Aj+1)/Tr=2ln|ad/aS|/Tr。这样就直接建立了阻尼系数n与供求弹性之间的关系。代入前述相应数据后，可以立即算出阻尼系数n=2ln|12/8|/2=0.40546（1/年），仍然与前述计算结果相同。当|ad|=|aS|时，价格系统将处于循环波动之中。当|ad|＜|aS|时，价格系统是发散的。只有当|ad|＞|aS|时，价格系统波动才是收敛的，这与前面蛛网模型的分析也是一致的。

8 结论

本文针对完全竞争农产品市场这一典型市场形态，运用完全的数理分析方法，实证分析了西瓜的生产和销售中的价格波动过程，剖析了价格形成机理，得到了一些有趣的结论。其动态分析以二阶微分方程作为价格波动的主要数学模型，是较为全面和准确的。它虽不能准确解释现实生活中更多的经济现象（因其影响因素众多，太复杂），但作为一种基本数理模型，二阶微分模型还是揭示了价格波动的本质的，是在一种理想状态中反映价格周期性波动情况的。该法为市场供求关系中的价格动态均衡分析带来了新思路，并为价格均衡的数理分析增添了新方法。

[1]罗纳德.肖恩（英）.，动态经济学[M].吴汉洪等译北京：中国人民大学出版社，2003.

[2]冯涛.微观经济学[M].西安：陕西人民出版社，2001.

[3]张金水.应用微观经济学[M].北京：清华大学出版社，2001.

[4]郑玉歆.中级微观经济学[M].北京：经济管理出版社，2004.

F016

A

1002-6487（2013）14-0058-04

（责任编辑/亦 民）