我国燃油期货市场的波动率预测模型

吴晓雄

（西南交通大学经济管理学院，成都 610031）

我国燃油期货市场的波动率预测模型

吴晓雄

（西南交通大学经济管理学院，成都 610031）

准确描述和预测石油及其相关产品的价格波动对各国政府能源政策的制定以及能源风险管理工作意义重大。文章以上海期货交易所燃油期货的15分钟高频价格数据为例，实证计算了三类代表性波动率模型：已实现波动率模型、随机波动模型以及GARCH族模型对我国燃油期货价格波动的预测值，同时，采用多种损失函数对比了三类波动率模型。实证结果表明，基于高频数据的已实现波动率模型对我国燃油期货市场具有最好的波动预测精度。而就基于日数据的模型而言，随机波动模型要明显强于GARCH族模型。

燃油期货；已实现波动率模型；随机波动模型；GARCH族模型；波动率预测

0 引言

目前，国外学者对能源价格波动的相关研究已有不少，Cabedo and Moya[1]以1992～1999年布伦特原油（Brent oil）现货价格的日数据为样本对原油价格波动率进行了刻画和预测，他们发现ARMA模型要优于标准的历史模拟法和方差－协方差方法。Giot and Laurent[2]以1987～2002年布伦特原油和西得克萨斯中质原油现货价格为样本，实证发现了ARCH模型的波动率预测精度更高。而Sadorsky[3]却认为以上学者使用的样本数据和模型种类过于稀少，所以他的研究以NYMEX交易的西得克萨斯中质原油、燃料油、无铅汽油和天然气期货价格的日数据为样本，检验了随机游走模型等12种模型的波动率预测精度。其研究结果显示：TGARCH模型能更好的刻画和预测取暖油期货和天然气期货价格的波动率；GARCH模型对原油期货和无铅汽油期货波动率的预测精度最高；只要选择合适的滞后阶数，简单的移动平均模型在某些情况下的波动率预测精度也表现地十分良好；尽管状态空间模型、向量自回归模型和二元GARCH模型存在更高的复杂性，但它们对上述能源市场波动率的预测精度却不及标准GARCH模型。

需要指出的是，国外学者对采用哪类波动率模型来预测石油及其相关产品的波动率并未得到一致结论。同时，更为欠缺的是，这些研究都没有利用到市场交易的高频数据。然而，毋庸置疑，高频价格数据往往蕴涵着更丰富和准确的市场波动信息。所以，已有工作的研究结论还有待于在更全面的波动率模型框架内加以检验。

本文以上海期货交易所燃油期货价格数据为研究样本，深入探讨各类代表性波动率模型预测我国能源期货市场波动的准确性，进而为市场风险管控提供更科学合理的决策依据。本文的研究特色为：（1）首次使用沪燃油期货价格的15分钟交易数据，对其定量波动特征进行深入分析；（2）全面将主流的三类代表性波动率模型：已实现波动率（Realized volatility，RV）模型、随机波动（SV）模型以及各种线性和非线性GARCH族模型纳入对比范围，并运用滚动时间窗的样本外波动率预测技术，计算了各类模型的实际预测结果；（3）通过改进对已实现波动率（RV）的估计，并运用更全面的损失函数（MSE、MAE、HMSE、HMAE、QLIKE和R2LOG），详细比较了不同模型对我国燃油期货市场波动率的刻画和预测能力。

1 样本数据和已实现波动率

1.1 数据说明

本研究以上海期货交易所燃油期货交易价格的15分钟数据为研究样本，以成交量为权重加权平均全部期货合约价格得到连续的价格序列，时间从2007年11月1日到2010年6月11日，共N＝637个交易日。因为每个交易日包含15个15分钟交易数据，所以全部样本共有9555个观测值，记为 It,d，t＝1,2,…,N，d＝1,2,…,15，其中 It,15表示第t个交易日的收盘价，样本数据来自文华财经系统。

本文日收益率R采用如下方法计算：

类似的，第t个交易日的（每15分钟）高频收益率（High-frequency return）Rt,d定义为：

1.2 已实现波动率的估计方法

为了比较不同波动率模型，需要一个经济变量能够客观代替真实市场波动率。Andersen等人[4]认为将日收益率的平方替代实际的日波动率会产生严重误差。因为市场的真实波动率是不可观测的，所以目前一般将已实现波动率作为市场真实波动率的代理变量。

Andersen and Bollerslev[5]提出，可以将第t天内所有高频收益率的平方和定义为第t天的已实现波动率，即：

然而，最近Hansen and Lunde[6]又指出，虽然高频数据可以反映交易时段期间的（Active）市场波动，但是无法提供非交易时段的波动信息（市场从第一天收盘到第二天开盘的波动率，即“Close-to-Open”波动率）。因此，Hansen and Lunde[6]建议可以用尺度参数δ对RV′进行变换使已实现波动率能更好地刻画真实市场波动。这样，第t天的已实现波动率为：

表1 日收益率序列和已实现波动率RV序列的描述性统计

表1显示所有序列（日收益率Rt、收益率平方Rt2、已实现波动率RVt和对数RV）t的超额峰态系数和Jarque-Bera统计量都很显著，表现出明显的“尖峰胖尾”和非正态性特征。这说明上海期货交易所燃油期货的波动幅度较为剧烈。同时，对Rt2、RVt和lnRVt序列而言，滞后5、10和20期的Q统计量在1%水平上显著，这说明在很长的时间内，上海期货交易所燃油期货的波动存在较为显著的持续性或长期记忆性特征。同时，ADF和P-P单位根检验均拒绝单位根存在的原假设，说明了各序列是平稳的时间序列，接下来可以直接建模。

2 波动率建模

2.1 已实现波动率模型（RV）

Andersen等人[7]的研究发现长记忆性时间序列的动力学特征使用“自回归分整移动平均模型”（ARFIMA）刻画更好。由于滞后不同阶数的ARFIMA(p,d,q)模型对其估计的结果非常接近[8]，因此，根据模型估计的AIC大小，我们这里采用ARFIMA(1,d,1)模型为上海期货交易所燃油期货的已实现波动率序列建模。进一步，Andersen等人[7]的研究指出，对数形式的已实现波动率序列（lnRV）t比原序列（RV）t具有更加平稳的统计特性（如表1中lnRVt的标准差、偏度和峰度指标都远小于RVt序列），因此更适合用ARFIMA对其建模。

ARFIMA(p,d,q)模型的一般形式为：

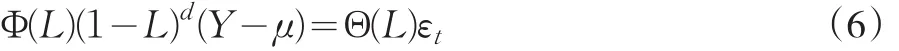
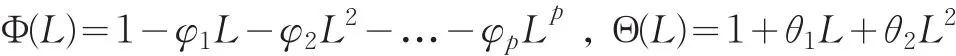
2.2 随机波动模型（SV）

首先，金融资产收益率如下表示[9]：

公式（7）中，μt是收益的条件均值，σt2是条件方差，新生量zt满足：zt～NID(0,1)。一般来说，收益率的条件均值很小，因此本研究都假定其等于零[8]。

SV模型中条件方差σt2是不可观测的，这与GARCH模型不同。条件方差满足如下随机过程：

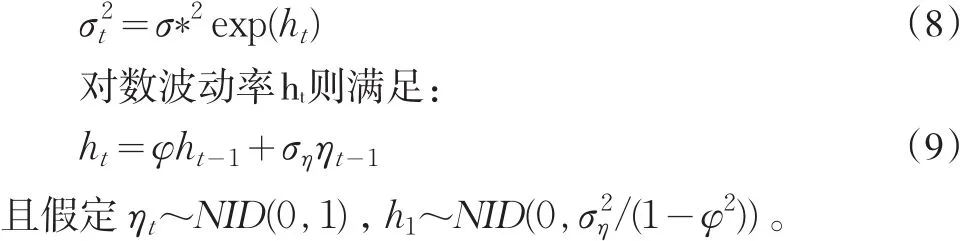
2.3 广义自回归条件异方差模型（GARCH）

标准GARCH(1,1)模型假定条件方差满足以下形式[10]：

而对于IGARCH模型来说，与GARCH(1,1)模型唯一不同的是它要求α+β＝1。基于金融市场的其它典型事实，学者们提出了更多形式的GARCH模型。本文考察的其它GARCH模型如下所示[11-14]：

GJR(1,1)：

其中，I(.)为指示函数，若()中条件成立，其值取1，否则取0。g为“非对称杠杆系数”。当γ＞0时，前一期的负收益率将导致更高的本期收益波动。

EGARCH(1,1)：

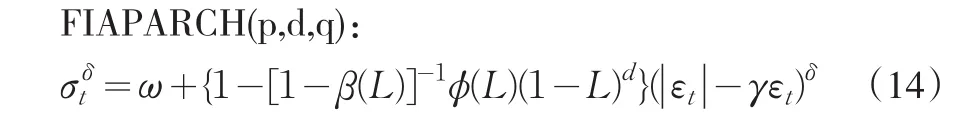
同样，我们采用FIAPARCH(1,d,1)的模型设定形式。

3 样本外波动率预测与模型预测能力检验

3.1 波动率预测方法

本文对以上讨论的三类主流波动率模型（ARFIMA-lnRV、SV、GARCH、IGARCH、GJR、EGARCH、FIGARCH和FIAPARCH）进行了滚动时间窗的“样本外预测能力检验”。预测方法的具体步骤为：首先，划分数据样本总体（t＝1,2,…,N＝637），使其分为“估计样本”和“预测样本”。其中，估计样本固定包含H＝425个交易日数据，最后的212个交易日数据则包含在预测样本中（即t＝H+1,H+2,…,H+M，其中M＝212）。然后，保持估计样本长度不变，连续向后滚动1天，每滚动1次，则重新估计模型参数，从而外推得到未来1天的波动率预测值。也就是说，我们对上述波动率模型分别重复估计了212次，获得了212个未来1天的波动率估计值，记为σˆm2，m＝H+1,H+2,…,H+M。已实现波动率的预测估计值记作RVm，1.2节详细说明了RVm的估计方法。已实现波动率的预测估计值可以替代真实市场波动率，以衡量各类波动率模型的预测精度。

3.2 模型预测能力评价

检验模型预测能力的一般方法是损失函数判断法。Hansen[11]认为应采用更多形式的损失函数作为模型预测精度的评判尺度。因此，我们采用了6种不同的损失函数，分别记作 Li，i＝1,2,…,6。L1和 L2分别为平均误差平方（Mean squared error，MSE）和平均绝对误差（Mean absolute error，MAE），是最常见的损失函数。L3和L4则分别表示经异方差调整的MSE和MAE（Heteroskedastic adjusted MSE and MAE）。鉴于本文篇幅，对L5和L6的解释详见Hansen[11]的研究。各损失函数如下所示：

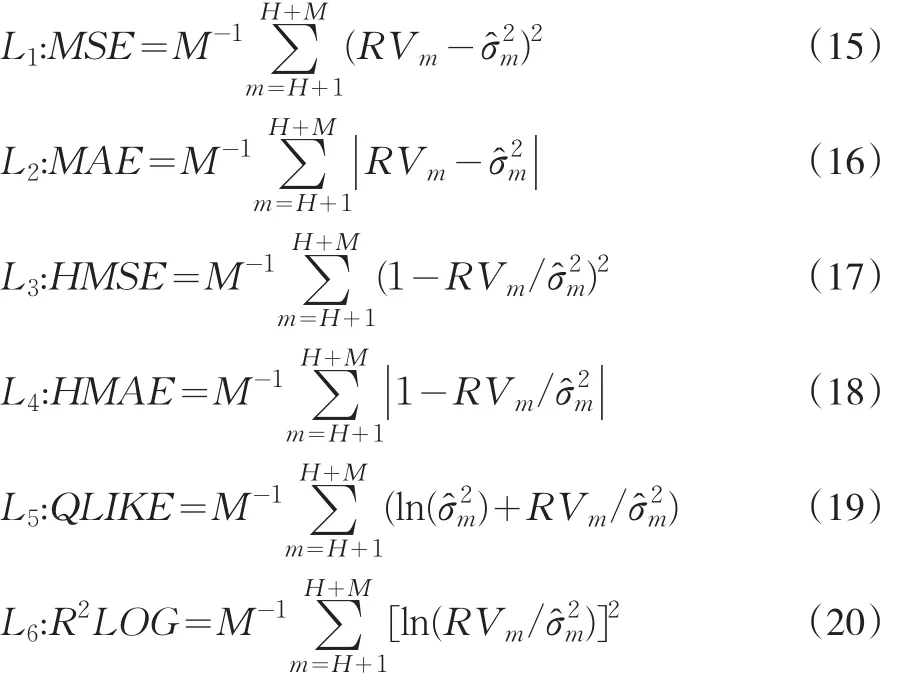
4 实证研究结果

4.1 波动率模型的样本外预测结果

图1（a）是ARFIMA-lnRV和SV模型的波动率预测结果（分别用实线和虚线表示），其预测样本区间为t＝426,427,…,637，共212天；小方块表示实际市场波动率的替代变量RV的估计值。图1（b）则显示的是标准GARCH和非线性的FIAPARCH模型的预测结果。

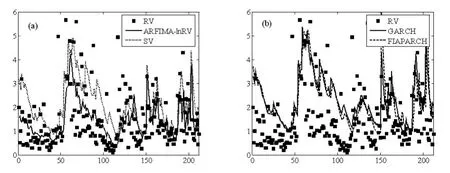
图1 不同波动率模型在预测样本区间的预测结果

从图1中（a）、（b）的对比可以发现，ARFIMA-lnRV和SV模型较为接近已实现波动率的估计，而GARCH族模型则有高估波动率的倾向。当然，定量的判断结果还需下面各类损失函数的具体计算。

4.2 各类波动率模型预测精度的检验结果

表2是基于各类损失函数的模型预测精度检验结果，某一损失函数标准下的最小、次小和第三小损失函数值用粗体上标的圆圈数字表示。

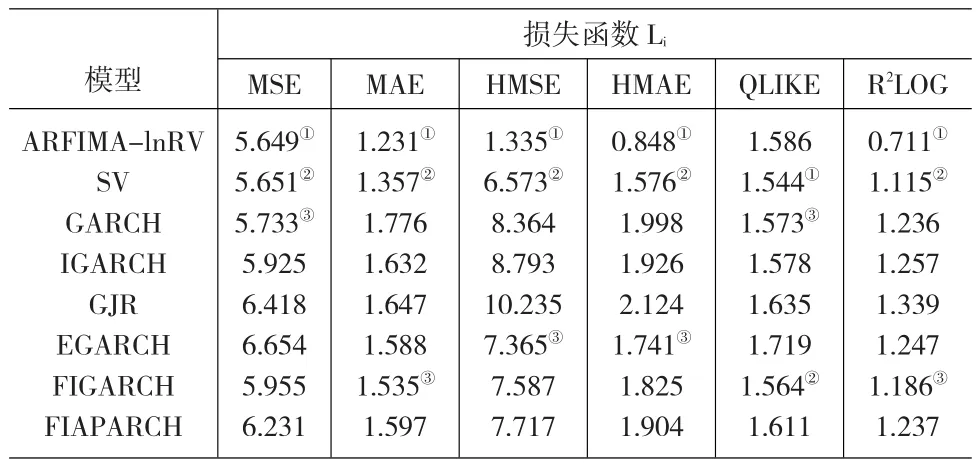
表2 各类波动率模型预测损失函数值

表2发现：（1）基于高频数据的ARFIMA-lnRV模型在5种损失函数（MSE、MAE、HMSE、HMAE和R2LOG）标准下都获得了最高的波动率预测精度。其中，在HMSE下，ARFIMA-lnRV模型的预测精度要远远高于其他对比模型。另外，虽然在QLIKE标准下，ARFIMA-lnRV的表现并非最好，但其获得的损失函数值与其他模型并未出现太大差距。（2）在上述同样的5种损失函数下，SV模型都表现出次优的预测精度，并且在QLIKE标准下，SV模型的预测精度是最高的。（3）总体来看，几乎没有哪一种GARCH模型获得了最优和次优的波动率预测精度（除FIGARCH模型在QLIKE标准下），这似乎也说明了对于刻画和预测我国燃料油期货市场的波动来说，各类线性和非线性的GARCH族模型均未表现出明显的优越性。

在原油市场波动率预测的研究方面，国内外相关学者采用的对比模型还主要局限于GARCH族模型内部，而我们的实证结果则对比了几乎所有研究中采用的GARCH族模型，同时加入了SV模型和基于高频数据的RV模型，因此我们的研究方法可以从更广的范围验证已有文献的结论。同时，由于我们对真实市场波动率的估计采用了基于高频数据的已实现波动率估计，因此本文的研究结论应该更加真实可靠。

综上所述，对于预测我国燃油期货市场的波动而言，基于高频数据的ARFIMA-lnRV模型最优。这意味着，相比日数据，高频数据的确包含更丰富的市场波动信息。所以，使用高频数据测度波动率应该可以为研究石油及其相关产品市场的定量波动特征提供更加可靠的依据。另外，同样是使用日数据，SV模型相比各类GARCH族模型具有更高的波动预测能力，所以我们认为，在大量股票市场研究中都表现出色的各种线性和非线性GARCH族模型也许并不适合我国燃油期货市场的波动率刻画和预测分析。在只能获取日数据的同等条件下，SV模型应该是波动率预测更好的选择。

5 结论与展望

以上海期货交易所燃油期货的15分钟高频数据为研究对象，本文运用滚动时间窗的样本外预测法，计算了三类代表性波动率模型：RV、SV和GARCH族模型（GARCH、IGARCH、GJR、EGARCH 、FIGARCH、FIAPARCH）在212个交易日内的样本外波动率预测。进一步，我们采用了6种不同的损失函数（MSE、MAE、HMSE、HMAE、QLIKE和R2LOG）来对比各类波动率模型的预测精度，以确保本文结论的准确性和稳健性。

我们的实证结果发现，基于高频数据的ARFIMA-ln-RV模型对我国燃油期货市场的波动率具有最优的预测精度。而就基于低频数据（日数据）的两类代表性模型而言，SV模型比各种常用的线性和非线性GARCH模型拥有更好的波动预测效果。这些发现提示我们，在股票市场研究中表现出色的GARCH族模型也许并不适合我国燃油期货市场的波动分析。进一步来说，高频数据中无疑蕴涵着更丰富的市场波动信息，因此使用高频数据测度波动率对挖掘我国燃油期货市场的波动信息意义重大。根据本文的研究结论，我国燃油期货市场的参与者可以更好地进行市场风险的管控。

[1]Cabedo J D,Moya I.Estimating Oil Price‘Value at Risk’Using the Historical Simulation Approach[J].Energy Economics,2003,25(1).

[2]Giot P,Laurent S.Market Risk in Commodity Markets:a VaR Ap⁃proach[J].Energy Economics,2003,25(1).

[3]Sadorsky P.Modeling and Forecasting Petroleum Futures Volatility[J].Energy Economics,2006,28(1).

[4]Andersen T G,Bollerslev T,Meddahi N.Correcting the Errors:Vola⁃tility Forecast Evaluation Using High Frequency Data and Realized Volatilities[J].Econometrica,2005,73(1).

[5]Andersen T G,Bollerslev T.Answering the Skeptics:Yes,Standard Volatility Models do Provide Accurate Forecasts[J].International Eco⁃nomic Review,1998,39(6).

[6]Hansen P R,Lunde A.Consistent Ranking of Volatility Models[J].Journal of Econometrics,2006,131(6).

[7]Andersen T G,Bollerslev T,Diebold F X,et al.The Distribution of Realized Stock Return Volatility[J].Journal of Financial Economics,2001,61(5).

[8]Koopman S J,Jungbacker B,Hol E.Forecasting Daily Variability of the S&P100 Stock Index Using Historical,Realized and Implied Vola⁃tility Measurements[J].Journal of Empirical Finance,2005,12(4).

[9]Taylor S J.Modeling Financial Time Series[M].Chichester:John Wiley and Sons,1986.

[10]Bollerslev T.Generalized Autoregressive Conditional Heteroskedas⁃ticity[J].Journal of Econometrics,1986,31(2).

[11]Hansen P R.A Test for Superior Predictive Ability[J].Journal of Business and Economic Statistics,2005,23(4).

F224

A

1002-6487（2013）14-0038-04

国家自然科学基金资助项目（71071131）

吴晓雄（1966-），男，江西九江人，博士研究生，研究方向：金融工程。

(责任编辑/亦 民)