考虑材料变形路径及应变率的车身前端吸能结构优化*

王金轮，兰凤崇，陈吉清

(华南理工大学机械与汽车工程学院，广州 510640)

前言

汽车发生正面碰撞时，主要由车身前端薄壁梁结构的塑性变形来吸收碰撞能量，其吸能特性和变形模式决定了车体在撞击时加速度或力的响应，对乘员保护有着非常重要的作用［1］。针对碰撞这类非常耗时的复杂非线性问题，国内外大部分学者的研究集中于单个薄壁件形状尺寸参数的优化，如文献［2］～文献［5］中通过近似模型与数值优化方法相结合对薄壁构件的几何尺寸和截面形状进行了抗撞性优化;文献［6］中通过逐次逼近近似模型与小种群遗传算法相结合对汽车纵梁前端的薄壁吸能圆管进行了形状尺寸参数的优化;文献［7］～文献［8］中采用响应面法研究了圆形和方形截面金属薄壁构件的端部锥形尺寸对抗撞性的影响。其设计变量局限于壁厚、长度和半径等几何参数，而且针对单个零件得到的优化参数应用到整车上时并不能保证整体结构性能为最优。另一方面，在涉及材料匹配优化的研究中，大多数研究仅仅以屈服强度作为设计变量，不能描述材料达到屈服强度之后的变形行为，由此引起的误差由图1可见一斑。该图示出车辆以48km/h初速度与刚性壁障100%正面碰撞3种仿真的吸能-时间历程，其中输入参数中屈服强度和应力-应变曲线是车身各零件材料标准拉伸试验得到的真实数据，应变率效应是利用Cowper-Symonds模型计入的。而且通常的做法是全部采用同一种材料，没有针对每个构件进行材料的优化选择，这样得到的结果不能保证是最优解，如文献［9］中采用支持向量回归方法和遗传算法相结合，在保证弯曲刚度及侧碰性能的前提下，实现了车身结构质量减轻5.44%。

为更好地发挥“合适的材料用于合适部位”的优势，本文中以车身前端主要吸能部件的材料和厚度为设计变量，进行连续变量与离散变量的组合优化，其中材料变量为可以描述其变形行为的有效应力-应变曲线，在整车100%正面碰撞环境中，针对每个所选构件进行材料和厚度的组合匹配;同时引入应变率效应来精确地描述材料在动静态条件下本构关系的差异，利用Cowper-Symonds模型(其中C=40.4，p=5［10］)近似插值得到的 B280/440DP 在不同应变率下的有效应力-应变曲线如图2所示，可见同一种材料在高应变率下其屈服强度和抗拉强度有明显的提高，碰撞过程中的应变率可达100/s，不考虑应变率效应将导致计算结果误差较大。本文中以比吸能、峰值碰撞力和平均碰撞力等作为耐撞性优化的评价指标，通过建立整车100%正面碰撞前端吸能区的简化模型，运用正交试验设计方法，在设计空间内对其耐撞性能进行仿真分析得到评价指标的响应值，构建了各个耐撞性评价指标关于设计变量的Kriging近似模型，并采用均方根误差RMSE验证了近似模型的精度，然后利用自适应响应面法进行优化求解。高强度钢板在抗撞性方面具有综合优势，由于在整车碰撞过程中材料发生破裂失效的变形情况比较复杂，本文中未考虑由于其延伸率较低而出现断裂和裂纹扩展导致吸能能力下降的因素。

1 100%正面碰撞简化模型

整车以48km/h的初速度与刚性壁障100%重叠正面碰撞，单元规模约为60万，整个碰撞过程持续约65ms，在8CPU工作站须运行10h，此有限元模型已经过侧碰和模态试验结果的验证，准确可信［11］。由于100%正面碰撞时主要以车身前端吸能区的压溃变形来吸收初始动能，A柱之后的区域基本未变形，所以考虑用一个附有质量、质心位置和极惯性矩的刚性壳单元来替代，100%正面碰撞简化模型如图3所示。整车与简化模型的碰撞仿真变形结果和前门槛中部的加速度-时间历程曲线见图4～图6，简化前后的加速度曲线基本吻合，变形情况和各部件的吸能曲线也基本一致，说明这种简化对100%正碰的影响很小，可用此简化模型进行后续的匹配优化。简化模型在相同工作站只须运行3h，可见简化模型在保证仿真精度的前提下有效缩减了计算时间。

2 车身前端结构的组合优化设计

2.1 设计变量

碰撞结束时，吸能最多的4个零件依次为前纵梁内板、吸能盒、保险杠和前纵梁外板，各主要吸能部件的吸能-时间历程见图7，大约共吸收了整车总能量的50%。如图8所示，在100%正面碰撞时车身前端3条能量传递路径中，保险杠→吸能盒→前纵梁内外板组成了车身前端最主要的能量耗散和传递路径，很大程度上决定了整车100%正面碰撞时的响应。根据文献［12］，一般在车身结构主要载荷传递路径上使用高强度钢板，以便碰撞力能够有效地分流和疏导，使碰撞能量得到有效吸收。因此选取此4个板件的材料和厚度作为设计变量(初始总质量为20.3kg)，即4个连续变量和4个离散变量，对材料进行编号，取5个离散的水平，分别代表5种屈服强度不同的高强度钢板，其有效应力-应变曲线见图9，通过定义材料Cowper-Symonds模型中C=40.4，p=5来计入应变率效应。各设计变量的初始值及水平见表1。

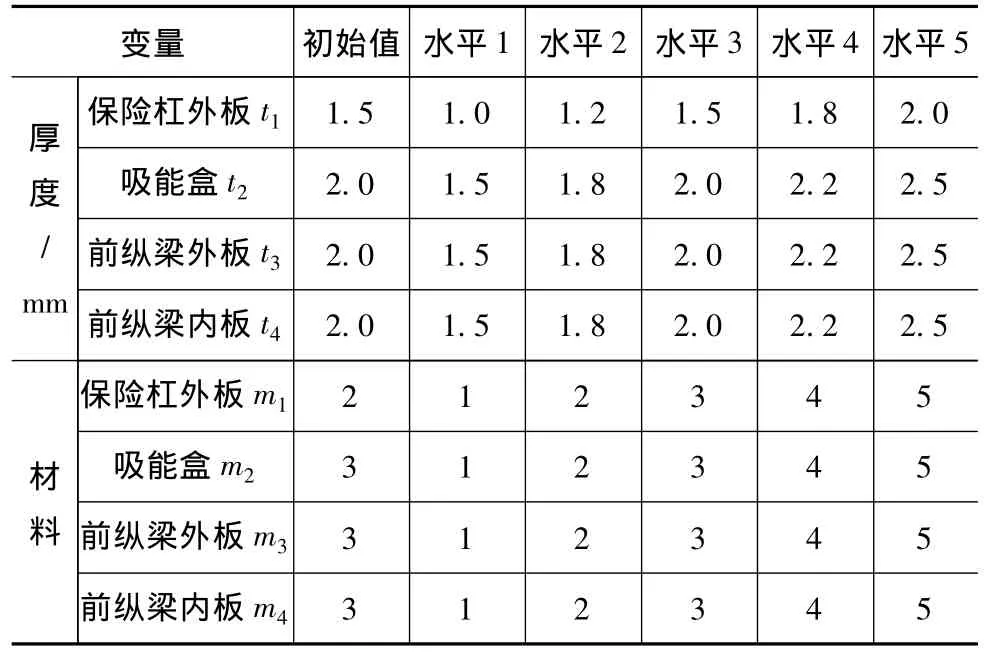
表1 材料和厚度变量的初始值及水平分布

2.2 优化目标

在整车结构安全设计中主要考虑使变形吸能部件在轻量化的同时最大可能地吸收能量，使整车B柱的加速度趋于平缓，且峰值尽可能小，同时尽量减小传递到乘员身上的载荷，从而达到保护乘员安全的目的［13］。因此，文中选取了比吸能、车辆与刚性墙之间的峰值碰撞力和平均碰撞力作为耐撞吸能性的评价指标。

(1)比吸能η

η为碰撞终了时单位结构质量所吸收的能量，即η=E/M

式中:E为结构吸能;M为结构质量。

(2)峰值碰撞力Fmax

碰撞仿真中主要考察的峰值碰撞力一般指结构刚开始产生屈曲时的临界值，它由结构的弹塑性屈曲决定。对于结构失效有重要意义，并在很大程度上决定乘员损伤的严重程度。由于在100%正面碰撞中前门槛中部的变形很小，输出此处的截面力曲线作为评价Fmax的依据。

(3)平均碰撞力Fmean

平均碰撞力是碰撞力曲线在压缩位移上的算术平均值，反映薄壁构件吸能的总体情况。对于理想的碰撞力曲线，Fmean与Fmax的差值越小，说明结构的吸能性能越好。

2.3 正交试验方案和部分仿真结果

由于设计变量涉及连续变量与离散变量的组合，利用正交试验表L50(511)设计了50次仿真试验，表2给出了前15次的设计变量取值和目标响应值。

表2 正交试验抽样样本点

2.4 Kriging近似模型及其精度验证

2.4.1 Kriging近似模型

在常用的近似模型构建方法中，多项式响应面近似模型对设计变量较少、非线性程度不高的工程问题具有较好的拟合效果;移动最小二乘法与径向基函数法对高度非线性问题有较高的拟合精度，但当离散点的数据量较大、形状较为复杂时，其对整个采样空间的拟合就可能产生很大的误差，导致近似模型失真;Kriging近似模型具有局部和全局估计的统计特性，使其在解决非线性程度较高的问题时比较容易取得理想的拟合效果，它通过对某一点已知信息加权的线性组合来估计这一点的未知信息，引进以距离为自变量的变异函数计算权值以保证估计值误差方差的最小化，既能反映变量的空间结构特性，又能反映变量的随机分布特性。整车碰撞仿真过程是一个高度非线性的动态过程，选择Kriging近似模型对采样点数据进行拟合是合适的。Kriging模型包含两部分:多项式和随机分布项，即响应值与自变量之间的数学关系式［14］为

式中:y(x)为待拟合的响应函数;f(x)为关于x的确定性函数，也称为确定性漂移，常常是类似于多项式响应面模型的多项式函数，代表设计空间的一个全局近似模型，即y(x)的数学期望(x);z(x)为一均值为零，方差为σ2，协方差不为零的随机函数。

2.4.2 近似模型的精度检验

依据图10所示的计算流程［15］，构建了比吸能、总质量、峰值碰撞力和平均碰撞力的Kriging近似模型。采用式(2)均方根误差RMSE验证近似模型结果见表3，可见近似模型有很高的拟合精度。

式中:εi为第i个估计点的误差;k为估计点个数。

表3 均方根误差RMSE

2.5 自适应响应面法和优化过程

2.5.1 车身前端结构组合优化的数学模型

根据已确定的设计变量、优化目标和约束条件，同时兼顾轻量化设计要求，建立该优化问题的数学模型为

2.5.2 自适应响应面法和优化过程

自适应响应面法的基本思想就是先通过较少的样本点构造1阶响应面，确定寻优方向，然后在优化过程中采用适当的步长沿响应面函数的梯度方向获得新的设计点，并将新的设计点引入设计空间，这样便可以逐步构造出2阶响应面模型，在后续的迭代中继续引入新的设计点来优化2阶响应面。假设依据P个样本点而求得2阶模型的回归系数向量为αP，已知矩阵为 XP，在此基础上新增一个样本点xP+1，其相应的响应值为yP+1，则已知矩阵XP+1［16］为

其中XT=［1，X(P+1)2，…，X(P+1)L］

新的回归系数向量αP+1的递推公式为

记CP=)-1，式中的 KP+1和CP+1可由以下递推公式计算:

该方法在迭代寻优的同时逐步引入新的设计点来修正响应面，直至寻优收敛。这种在优化过程中实时更新响应面近似函数的方法可提高寻优效率，而且可以得到更加精确的最优解。

利用自适应响应面法对所建立的Kriging近似模型进行优化，迭代历程见表4。经13次迭代后收敛，各目标响应的优化迭代历程曲线如图11～图14所示。通过对比优化前后的数据可知，优化后的比吸能比优化前提高15.9%，结构总质量比优化前减轻13.4%，峰值碰撞力比优化前降低29.7%。

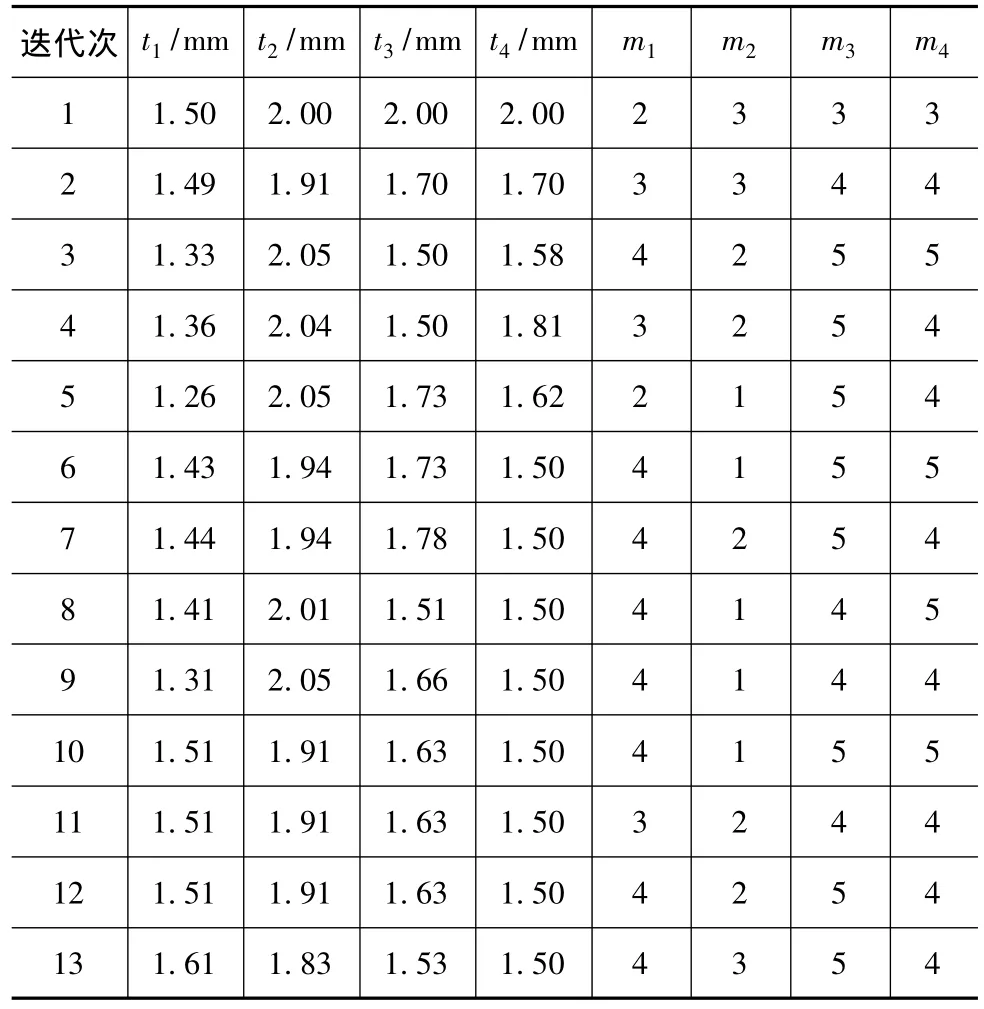
表4 基于自适应响应面法的迭代历程

3 优化结果的验证

为进一步验证优化方案的准确性，根据表4的优化结果并对厚度值进行圆整，在简化模型中将表1中的4个零部件的板厚和材料分别设置为1.6、1.8、1.5、1.5mm 和 B340/590DP、B280/440DP、780DP、B340/590DP，然后依据我国乘用车正面碰撞标准 GB11551—2003对优化后的模型进行正面100%刚性壁障碰撞仿真分析，碰撞初速度为48km/h。在仿真研究中，对于汽车正面碰撞安全性，主要通过加速度和乘员舱的变形量两个指标来评价［17］。优化前后的碰撞加速度曲线见图15，由于优化后的零部件厚度和材料分布更加合理，材料的吸能特性得到了更好的发挥，使碰撞加速度峰值由56.8g下降为38.7g，减小31.9%。

优化前后的数据见表5。优化后的4个板件总质量为17.5kg，减轻13.7%，而吸能量26.6kJ比优化前的26.4kJ略有增加，因此比吸能由1.30kJ/kg大幅增加至1.52kJ/kg。此外，前端缓冲能力的提升使传递到乘员舱的能量减少，乘员舱的变形相应减小。对乘员舱变形量的评价指标主要包括整车最大变形量、制动踏板后移量、前挡板后移量、转向盘中心的上移量和后移量，从表5可以看出，制动踏板后移量峰值和前挡板后移量峰值略有下降，其余3个指标略有上升，但变化不大。

表5 评价指标对比

优化前后的仿真结果表明，基于Kriging近似模型的自适应响应面法对厚度和材料混合变量的优化解有效可信，对于汽车研发过程中如何选用高强度钢板具有较好的指导作用。

4 结论

(1)建立了汽车前端吸能结构的简化模型，确保了100%正面碰撞仿真具有良好的精度，且有效缩减了碰撞仿真的时间，使开发阶段探索汽车前端结构吸能特性并进行优化成为可能。

(2)以车身前端4个主要吸能部件的厚度和材料为设计变量，尝试考虑材料变形路径和应变率效应的影响，使碰撞仿真过程更加贴近实际情况，设计了50组正交试验，得到了各采样点处的目标响应值;通过构建结构比吸能、总质量、峰值碰撞力和平均碰撞力的Kriging近似模型和数学优化模型，基于自适应响应面法获得了该问题的优化解。

(3)通过对比优化前后的仿真结果，验证了优化解的有效性。优化后前端结构的比吸能大幅提升，碰撞加速度峰值下降31.9%，而乘员舱侵入量峰值各指标变化不大，从而使整车100%正面碰撞的安全性有了较大提高。

［1］张维刚，廖兴涛，钟志华.基于逐步回归模型的汽车碰撞安全性多目标优化［J］.机械工程学报，2007，43(8):142-146.

［2］Redhe M，Forsberg J，Jansson T，et al.Using the Response Surface Methodology and the D-optimality Criterion in CrashworthinessRelated Problems［J］.Structural and Multidisciplinary Optimization，2002，24:185-194.

［3］Forsberg J，Nilsson L.On Polynomial Response Surface and Kriging for Use in Structural Optimization of Crashworthiness［J］.Structural and Multidisciplinary Optimization，2005，29(3):232-243.

［4］Forsberg J，Nilsson L.Evaluation of Response Surface Methodologies Used in Crashworthiness Optimization［J］.International Journal of Impact Engineering，2006，32:759-777.

［5］Lee S H，Kim H Y，Oh S I.Cylindrical Tube Optimization Using Response Surface Method Based on Stochastic Process［J］.Journal of Materials Processing Technology，2002，130-131:490-496.

［6］张勇，陆勇.基于近似模型技术的圆管耐撞性优化设计［J］.华中科技大学学报(自然科学版)，2010，38(9):129-132.

［7］侯淑娟，李青，龙述尧.端部圆锥形薄壁构件的抗撞性设计优化［J］.湖南大学学报(自然科学版)，2006，33(3):37-40.

［8］侯淑娟，李青，龙述尧.端部方锥形薄壁构件的抗撞性尺寸优化［J］.机械强度，2007，29(4):682-685.

［9］施颐，朱平，张宇，等.基于刚度与耐撞性要求的车身结构轻量化研究［J］.汽车工程，2010，32(9):757-762.

［10］王国春，成艾国，高晖，等.材料应变率对汽车碰撞性能影响的研究［J］.汽车工程，2010，32(6):482-485.

［11］谢然，兰凤崇，陈吉清，等.满足可靠性要求的轻量化车身结构多目标优化方法［J］.机械工程学报，2011，47(4):117-124.

［12］兰凤崇，钟阳，庄良飘，等.基于自适应响应面法的车身前部吸能部件优化［J］.汽车工程，2010，32(5):404-408.

［13］王海亮，林忠钦，金先龙.基于响应面模型的薄壁构件耐撞性优化设计［J］.应用力学学报，2003，20(3):61-65.

［14］李铁柱，李光耀，陈涛，等.基于Kriging近似模型的汽车乘员约束系统稳健性设计［J］.机械工程学报，2010，46(22):123-129.

［15］张勇.基于近似模型的汽车轻量化优化设计方法［D］.长沙:湖南大学，2009.

［16］廖兴涛，张维刚，钟志华.响应表面法在薄壁构件耐撞性优化设计中的应用研究［J］.工程设计学报，2006，13(5):298-302.

［17］张维刚，刘晖.Kriging模型与优化算法在汽车乘员约束系统仿真优化中的应用研究［J］.湖南大学学报(自然科学版)，2008，35(6):23-26.