汽车零部件物流越库配送系统的多重响应优化*

施 文，刘志学，刘 林

(华中科技大学管理学院，武汉 430074)

前言

对汽车制造企业而言，汽车零部件物流由入厂物流(供应物流、采购物流)、生产物流和出厂物流(售后物流)组成，其中入厂物流是最重要的环节，它是连接供应商与装配企业之间物料供应活动的重要来源。目前，国内汽车制造企业零部件入厂物流大多采用基于第三方物流(third-party logistics，TPL)的循环取货越库配送物流模式［1］。越库中心(cross-docking center，CDC)也称集配中心，是该模式中的重要物流节点，发挥着巨大的规模经济的作用。据《中国汽车行业发展报告2010》预测，未来10年内，国内汽车需求增长率将保持在10%左右。在此利好形势下，众多汽车制造商纷纷设立新厂，如武汉的东风乘用车﹑神龙汽车和东风本田三大整车厂。产能的扩大势必带来零部件物流量的增加，这对CDC提出了更高的要求，如何优化配置CDC以适应新的物流需求是TPL的一项重要任务。

国内外许多学者展开了越库配送问题的研究。文献［2］和文献［3］中介绍了日本汽车零部件物流越库策略实施的成功经验，但未提出任何优化模型。有关越库的技术性研究始于20世纪90年代，部分学者研究了战略层面的越库配送问题，主要指CDC作为供应链某一层级的网络选址和越库中心内的布局设计。文献［4］中将CDC放入供应链环境中加以研究，解决了生产、物流和外包运作的设计问题;文献［5］中针对该问题提出了一种新型的启发式算法。文献［6］中针对零售型与转运型两类越库，探讨了越库的形状设计问题。有关越库的策略层研究集中在车辆路径与库台分配问题。文献［7］和文献［8］中将越库与车辆路径问题联合考虑，采用禁忌搜索算法找出车辆数和最优的车辆路径调度，以最小化总的运输成本和车辆固定成本。文献［9］中研究了韩国的邮政配送中心的库台分配问题，其目的是将发货区库台按目的地进行分组划分。文献［10］中针对长方形越库中心的库台二次指派问题(quadratic assignment problem，QAP)提出一种新型混合整数规划模型，作者将模拟退火算法的结果应用于Con-way公司的越库。大部分学者对车辆到达越库时的调度问题展开研究，它属于运作层问题。文献［11］中最早展开了此类问题的研究。文献［12］中建立了一类特别的带有传送带的越库系统模型，在该模型中卸载区库台仅服务一个装载区库台。文献［13］中研究了单库台越库的车辆调度问题，他们将越库作业比作两阶段机器作业模型，通过优先权约束(precedence constraints)将越库入库作业视为第一阶段，出库作业视为第二阶段。文献［14］中研究了多库台的情形。

上述文献从不同层面研究了越库的实施问题，集配型越库作为越库实施的重要类型，在汽车零部件物流中发挥着巨大的规模经济作用，但未发现针对汽车行业CDC内部设计的优化研究。从建模方法上看，大部分文献采用解析法建立越库模型，由于该问题大多为NP-hard或NP-complete，其求解算法一般为启发式或元启发式算法，但许多模型结构停留在较少出入库库台或无暂存区的情形［11-14］，这与现实情形相差较远，实际中库台数一般为6～200个［15］，作者所调研的东本储运和长安民生的库台数目约为10个。因此，本文中基于CDC实际运作构建了复杂的离散动态系统仿真模型，然而，仿真仅是一种实验手段，无法给出产能扩大后TPL最佳的改进方案。为此，本文中将CDC仿真模型与响应面法(response surface methodology，RSM)相结合，深入分析CDC物流运作的最佳改进方案，为TPL运作决策的调整提供可靠的解决思路。

1 问题描述

国内绝大多数汽车零部件供应商分布于珠三角、长三角和环渤海湾三大汽车产业带，而某些主机厂(assemble plant，AP)位于距离较远的中西部地区，如东风本田、东风神龙和长安福特等，并且通过合资的方式成立了为其服务的TPL，如东本储运、捷富凯-鸿泰和长安民生等。从规模经济角度考虑，TPL在各汽车产业集聚区设立CDC。汽车制造商、零部件供应商与TPL事先签订合作协议，委托TPL实施零部件物流Milk-run，即根据零部件供应商的分布、零部件的补货频率、补货数量、需求特征和对生产的重要性等因素，划分若干Milk-run区域。图1展示了整个TPL-MRCD物流流程，通常情况下，从某个Milk-run取货的零部件数量不够整车(less-thantruckload，LTL)，因此该车将LTL零部件先运输至区域CDC(支线运输)，经过一定时间的集并，再将装满零部件的整车(truckload，TL)运输至厂边仓库，最终到达主机厂(干线运输)。

图1中间部分展示了CDC内部的基本结构。库台(doors)是卸载区(receiving dock)和装载区(shipping dock)最主要的组成部分，一般地，单个库台仅容纳一辆货车。一旦入库车辆(inbound trucks，IBT)即图1中卸载区卡车抵达CDC，调度室视库台的繁忙程度决定该车辆下一位置，若卸载区有空闲库台，入库车辆则随机分配至其中之一;相反，若卸载区库台已全部占用，入库车辆则先进入车辆等候区等待，直到某一库台空闲。入库车辆停靠在库台时，操作工人分派至此卸货扫描。扫描完成后，零部件根据装载区出库车辆(outbound trucks，OBT)的到达情况决定下一步的路线。路线1:若装载区库台停靠有OBT，则零部件通过传送带直接运至装载区，其中，卸载区库台与传送带间及传送带与装载区间的两段运输由叉车完成;路线2:若装载区库台未停有OBT，零部件则由叉车先运至暂存区暂存，待OBT到达后，再由叉车运至该OBT停靠的库台。由于路线2的零部件有一定存储时间，故装载区优先选择路线2的零部件。零部件在装载区装至满载后再干线运输至厂边仓库。此外，零部件不允许在CDC暂存区存储太长时间，一般不超过24h，否则由额外的货车将其运至厂边仓库。

由于中国汽车需求增长迅速，大部分汽车生产商更关注其产量与零部件供给的时效性，这一论点也得到所调研企业管理者的认同(东本储运和长安民生)。本文中以CDC零部件吞吐量(total throughput，TT)与平均流程时间(operation time，OT)作为系统绩效指标。TT是衡量CDC作业能力的重要指标，其选取符合国内汽车行业的实际背景;OT则是衡量CDC作业效率高低的标准，随着汽车制造商产量的扩大，需要远距离供应商配合准时(just-intime，JIT)生产，实施JIT配送，这对零部件的流程时间提出了更高的要求，部分越库配送文献也以OT作为目标函数。

2 CDC仿真模型

2.1 逻辑模型

利用Rockwell公司开发的面向对象的仿真平台ARENA 13.0作为仿真工具［16］。为建模和测试的顺利进行，本文中将CDC模型分割为6个相互联系的子模型。

子模型1 卸载区模型

IBT到达CDC触发卸载区事件，该事件包括库台分配、零部件卸货和扫描3个子事件。卸载区的库台数为NRDC(下标C表示CDC)，若IBT到达时处于忙态的库台超过NRDC，则该IBT先到车辆等候区排队等待，直到空闲库台出现，默认情况下等待区服务规则为先到先服务(FIFO)。每一库台配备足够数量的作业工人，单位数量零部件卸货时间UTC服从参数为(aUTC，bUTC，cUTC)的三角分布。因此，某辆IBT的卸货时间为UTC·QLTL，其中QLTL为支线运输装载量。扫描与卸货在卸载区库台同步进行，包装的朝向错误或标签损坏时有发生，需要工人二次扫描或手动输入条码，单位数量零部件扫描时间STC服从参数为(aSTC，bSTC)的均匀分布，一次扫描通过率为β，第二次操作时间与第一次相同。零部件下一步路线取决于卸载区是否停靠有OBT，若有，则零部件直接进入传送区由传送带运至该OBT，否则进入暂存区存储。

子模型2 传送区模型

传送带为不可聚集式输送设备，即传送带上被输送的零部件空间间隔不会改变。传送区传送带数量为NCC，传送带的长度均为CLC，传送速度为CVC。传送带由许多不断移动的等长单元组成，该单元容纳不多于一个单位的零部件，假设零部件平均单元大小为CSC，则单位零部件在传送带上所占的平均尺寸为CSC。

子模型3 暂存区模型

若装载区未停靠OBT，零部件则先转移到暂存区直到OBT到达，暂存区的固定容量为CC，暂存区中的零部件服从FIFO排队规则，即优先装载存储时间较长的零部件。若零部件在暂存区的逗留时间超过门槛值TT，而此时仍无到达的OBT，这些零件由额外的OBT*直接运至主机厂(非厂边仓库)，OBT*为TPL再外包的运输车辆，该部分零部件不计入系统绩效。此外，暂存区的零部件比传送区的具有更高的优先级，即OBT优先装载暂存区零部件。

子模型4 叉车与拖车模型

叉车和拖车是CDC内部的两种运输资源，负责零部件在卸货区、传送区、暂存区和装载区4个站点间的物流，站点间的距离等于DC(x，y)，其中x≠y=r，s，c，t，式中 r为卸货区，s为装载区，c 为传送区，t为暂存区。叉车和拖车数量分别为NFC和NTC，运输速度为FVC和TVC，每车运输容量为FCC和TCC。叉车和拖车在运输能力上有所差别，故优先选择叉车作业，且DC(r，t)和 DC(t，s)较远，这两段运输仅能用叉车完成。

子模型5 装载区模型

装载区库台数等于NSDC，若OBT到达时，装载区无空闲库台，则OBT到车辆等待区排队等待，默认情况下等候区排队规则为FIFO。库台配备相应数量的操作工人，整车OBT的零部件装载量为QTL，单位数量零部件装载时间 LTC服从参数为(aLTC，bLTC，cLTC)的三角分布，因此，每辆OBT的装载时间为 LTC·QTL。

子模型6 控制逻辑模型

在这个子模型中，实体没有相应的物理意义，被称作逻辑实体，它们被用来实现模型中的某种逻辑或改变系统状态，此处包括赋值与查找两个控制逻辑，每间隔1min，仿真系统自动查找暂存区中逗留时间超过门槛值TT的零部件，并将符合该条件的零部件清理出暂存区，即通过OBT*装载离开。

本文中模型为终态(terminating)仿真模型，其数据来源为作者调研的武汉某家汽车TPL企业。它所服务的汽车制造企业以30天为一个计划生产周期，因此，共有30个仿真日(每日工作12h，共360h)，另有5个仿真日的系统Warm-up时间。由于是随机性仿真，为提高仿真输出的精确度和实验设计的效率，每个仿真场景的重复次数为10。最终仿真模型的运行界面见图2。

2.2 CDC影响因子

影响CDC系统绩效(TT和OT)的因子主要包括收货区库台数、发货区库台数、传送带速度、传送带数量及存储区容量。为便于分析，5个因子用A，B，C，D，E 表示，利用式(1)将变量规范至［-1，1］之间，其中XHigh和XLow分别为因子的上下限，XActual为因子的实际值，Xi为规范后的值。表1给出了5个因子的取值范围，数据来源于所调研的武汉某汽车TPL企业。低水平为企业现有状况，高水平代表主机厂产能扩大后TPL的预测值。

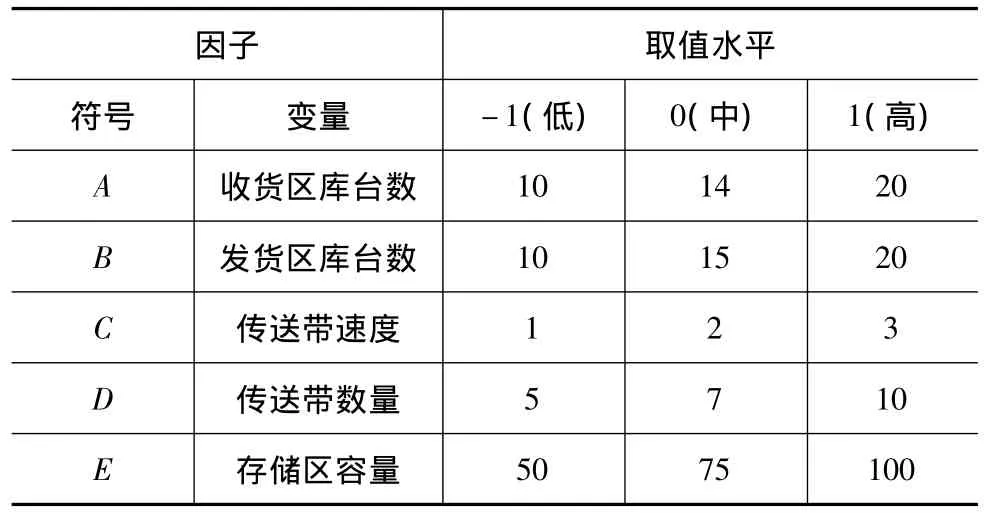
表1 CDC仿真模型绩效影响因子和因子取值水平

3 建模及优化步骤

3.1 建立响应面元模型

上述CDC仿真模型仅是一种实验手段，并未给出任何优化方案。本文中基于CDC仿真模型，建立响应面RSM元模型，RSM是一种通过估计参数组合，使给定目标函数达到最小的启发式优化方法。与其它仿真优化方法相比，RSM需要相对较少的仿真重复和因子组合，并且与昂贵仿真(单次仿真运行需要大量时间)运行所需的时间相比，RSM启发式搜索所需的数学和统计计算时间可以忽略［17］。在供应链类似的仿真系统中，文献［18］～文献［20］中将RSM与仿真模型相结合解决了地铁线及生产线的优化问题。在汽车的结构设计中，文献［21］～文献［22］中基于RSM优化了车身接头和结构振动的频率问题。本文中首次将其应用于汽车零部件物流的越库中心设计，并且所优化的响应具有多重性。

响应(OT与TT)与自变量(CDC的影响因子)的关系形式未知。RSM的第一步就是寻求响应y与自变量集合之间真实函数的一个合适的逼近式。一般讲，可用在自变量某一区域内的一个低阶多项式来逼近，通常为2k全析因设计或分式析因设计，若响应适合自变量的线性函数建模，则近似函数为1阶模型:

式中:xi为 m 维自变量的第 i个分量;β0、βi、βij为未知参数，通过仿真实验由最小二乘法求出;ε为模型的随机误差项。若方差分析显示系统有曲度出现(P-value＜显著性水平)，则必须用更高阶的多项式，一般为2阶模型:

由于中心复合设计具有可旋转性和球面性等优点，常用于拟合2阶响应面，它包括2k全析因设计，2k次轴点设计以及nc次中心点设计，轴点为(±α，0，0，…，0)，(0，±α，0，…，0)，(0，0，±α，…，0)，…，(0，0，0，…，±α)。

3.2 多重响应优化

由于模型所优化的响应具有多重性，即OT与TT。因此，本文中采用Derringer-Suich的满意度函数法，该方法首先将响应yi转换为单个满意度函数di，其变化范围是0≤di≤1。如果响应yi是它的目标值，则di=1;如果响应在可接收的范围之外，则di=0。

如果响应y(TT)的目标T是一个最大值，则

当权重r=1时，满意度函数是线性函数。若选择r＞1，则更强调靠近目标值;若选择0＜r＜1，则目标值较不重要。如果响应y(OT)的目标是一个最小值，则

式中L和U分别代表仿真中响应的最小和最大值。选择设计变量，使之最大化m个响应的总满意度:

4 仿真实验与优化

4.1 拟合响应面元模型

共进行44次仿真实验，包括25次全析因设计，10次轴点设计和2次中心点设计。在显著性水平为0.05的条件下，TT与OT的2阶响应面元模型最为显著，见表2。最终模型为式(7)～式(10)。实际变量方程式(8)和式(10)虽有实际意义，但规范变量方程能识别影响系统绩效的重要因子，根据式(7)和式(9)，影响TT的因子重要性排序:C＞＞B＞E＞A＞D，影响OT的因子重要性排序:C＞＞A＞B＞E＞D。可见，因子C是影响系统TT和OT最为重要的因子，其变化将极大地影响系统绩效，在主机厂产能增大后，TPL应优先改进传送带的性能，实际加快零部件在CDC内的库内物流。此外，适当增加CDC的库台数对绩效改进也有一定的帮助。

TT规范变量方程:

TT实际变量方程:

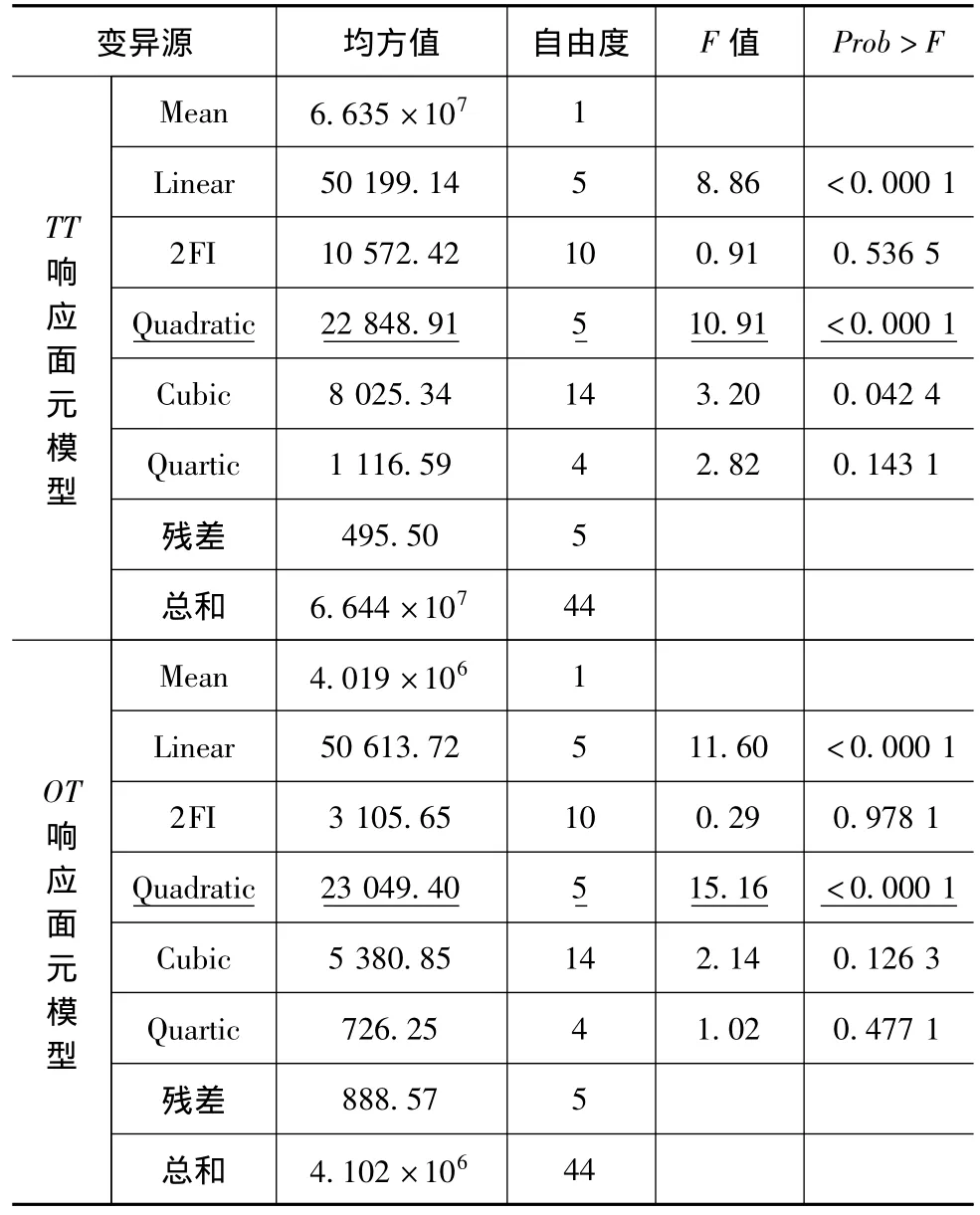
表2 2阶响应面元模型拟合

OT规范变量方程:

OT实际变量方程:

表3和表4为TT和OT 2阶响应面元模型的方差分析表。由表3和表4可知，R2与Adj R2都处于较为理想的状态，所拟合的响应面元模型能分别解释仿真模型吞吐量与运作时间0.8967与0.9165的变异性，说明该模型能较好地代表仿真系统，拟合的RSM元模型(式(7)～式(10))可用于优化响应TT和OT。

4.2 多重响应优化

本模型的目标为同时优化TT和OT，参见式(6)，即 D(x)=Max{d1·d1))}1/2，结合表1因子的取值水平和式(7)～式(10)，将多重响应优化问题转化为非线性规划的求解问题。除多重响应优化外，还考虑了仅优化单个绩效TT和OT时的最优因子水平。3类绩效目标包括:①OT达到正常水平下最大化TT;②TT达到正常水平下最小化OT;③同时优化OT与TT。表5展示了目标函数与最优解的取值。可以看出，与现有(低)水平(调研的结果)相比，优化结果中除收货区库台数不变外，其余4个因子都有所提高，这与该TPL企业的预测结果基本吻合，说明仿真模型具有较高的效用和效力，优化结果切实可行。此外，4因子(除收货区库台)的最优取值未达到该变量预测的上限，说明TPL企业盲目地扩大资源，即因子扩大至最高水平，将造成资源严重浪费。由于规模效用的原因使得优化的配置已能获得企业满意的绩效，而合理的资源配置也正是TPL企业希望看到的结果，因为与预测水平相比可以帮助企业缩减成本开支。

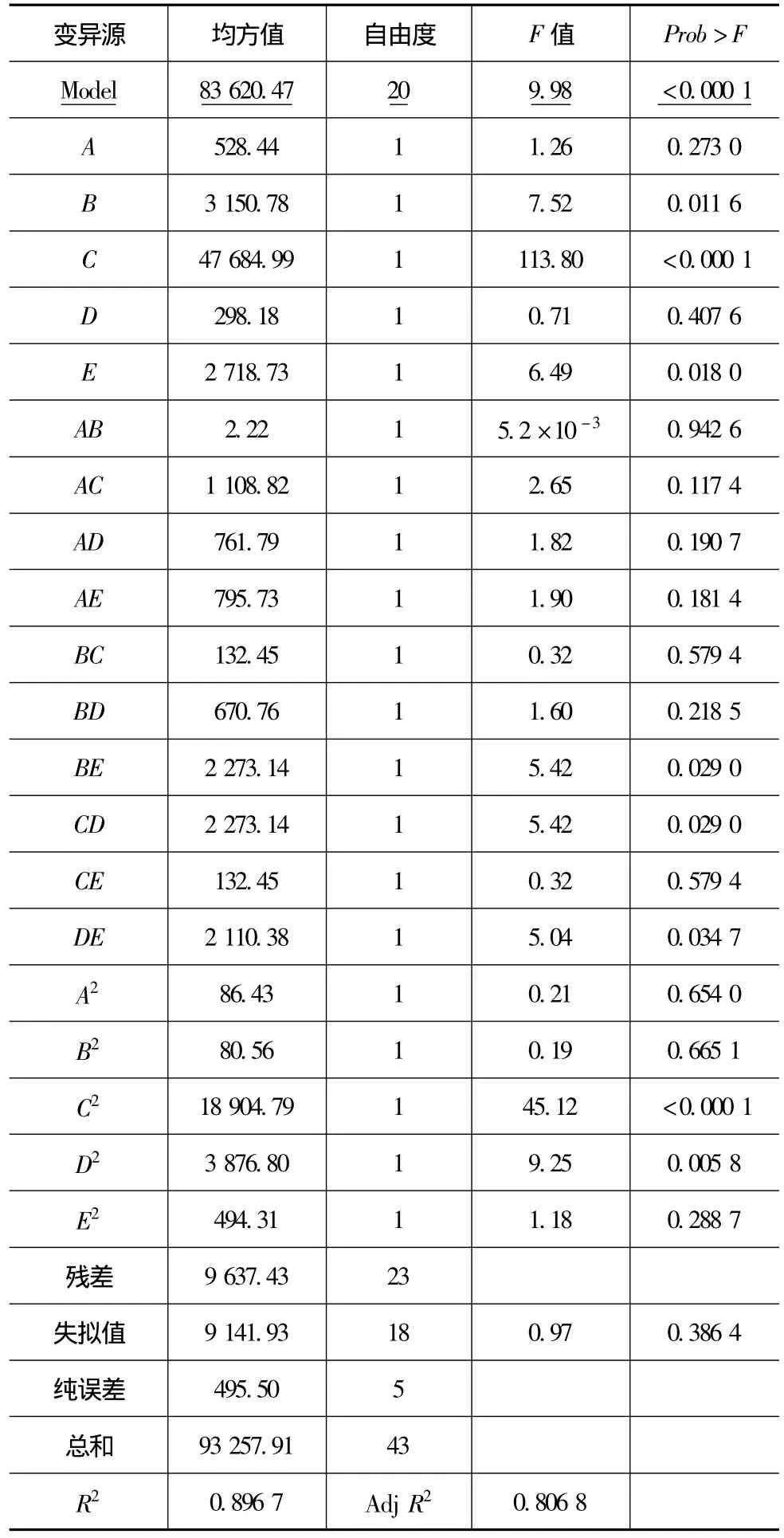
表3 TT响应面元模型因子方差分析表

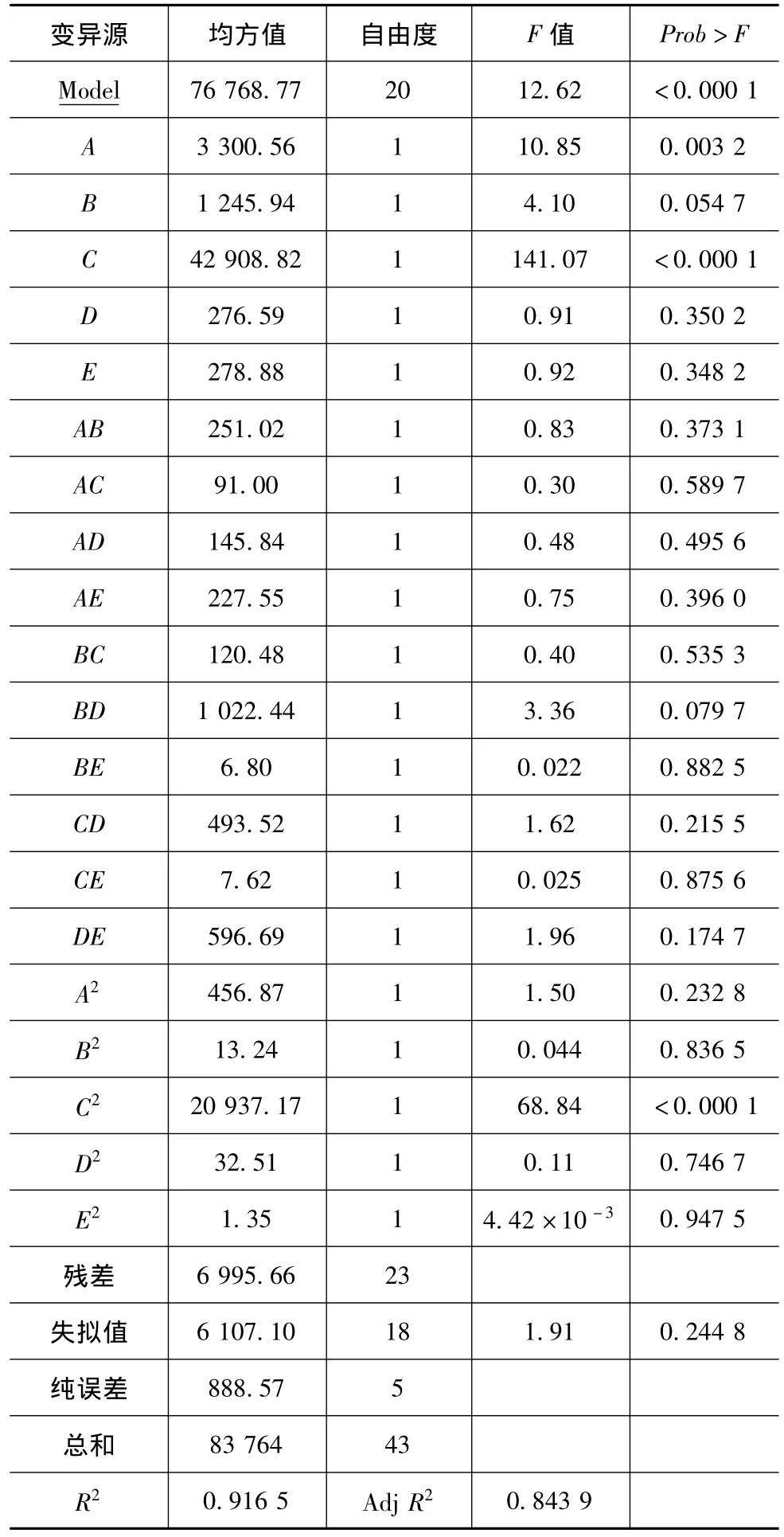
表4 OT响应面元模型方差分析表

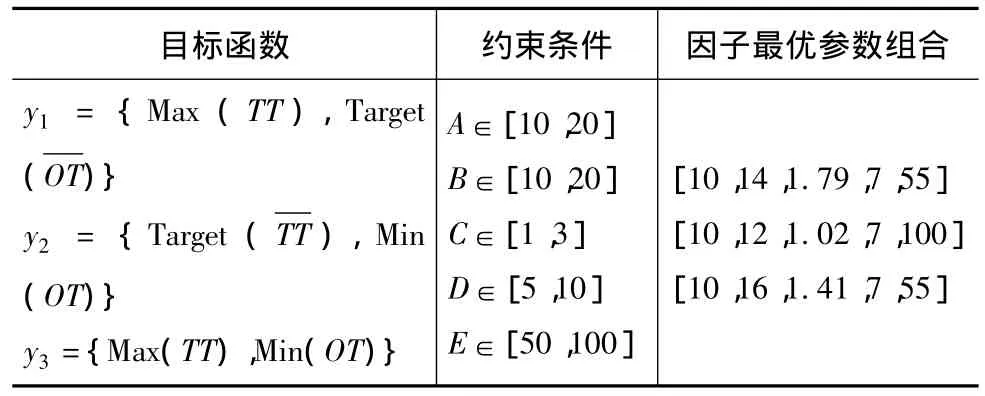
表5 3种目标函数及最优解

4.3 不同运作方案仿真结果比较

对3组优化因子组合重复25次仿真实验，表6展示了表5中3种因子最优组合的平均仿真输出结果。由表可见:绩效目标y1与绩效目标y2对单独绩效的改进较大，在不延长运作时间的情况下，绩效目标一提高了2.9%的零部件吞吐量;绩效目标y2缩短了15.2%的零部件平均运作时间，但其也降低了1.7%的系统吞吐量;绩效目标y3同时改进了两类绩效，但其单个绩效的改进幅度小于前两种方案。TPL可根据其既定的目标选择相应的优化方案。

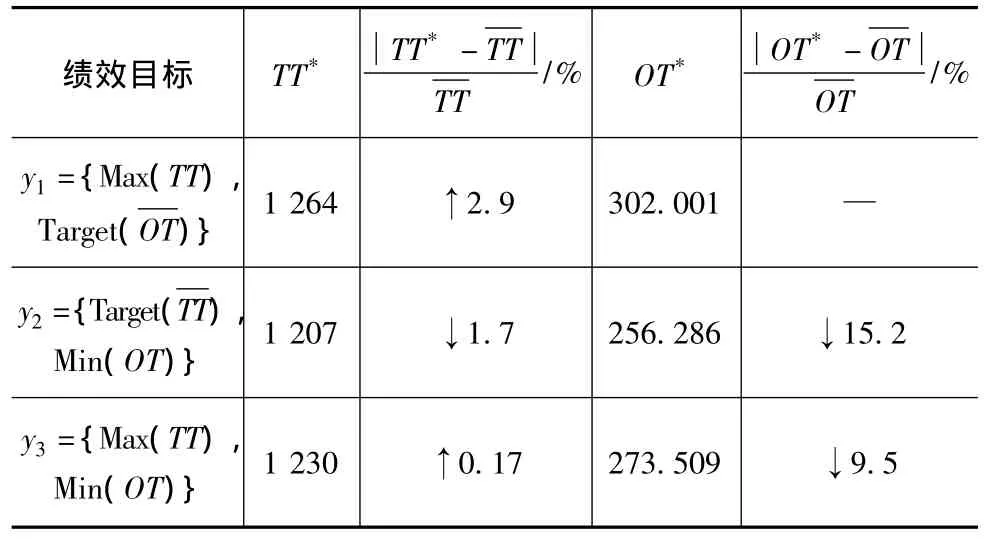
表6 3种绩效目标最优方案比较

5 结束语

针对汽车零部件物流越库系统动态性与随机性的特点，提出了一种离散事件系统仿真，实验设计及响应面元模型相结合的建模与优化技术解决该系统运作优化问题，为管理决策的制定提供了技术支持。仿真为解决复杂物流系统提供了有效的手段，在精细的越库系统仿真模型的基础上，建立了响应面元模型，该方法在后仿真分析中极大减少了仿真实验所需运行的次数，并便于灵敏度分析而无须重复实验。响应面拟合方差分析显示，元模型代表了高水平的仿真模型。最后的优化结果表明，越库系统性能获得明显改进，管理决策者可根据其既定的目标选择相应的优化方案。未考虑不可控因素对CDC绩效的影响是本文的一个主要不足，这也是今后值得研究的重要问题。不可控因素包括生产商发货车辆到达的平均间隔时间，零售商车辆到达的平均间隔时间等，这需要采用口田设计等稳健设计方法减少响应变动，降低其对系统绩效的影响。

［1］左晓露，刘志学，郑长征.汽车零部件循环取货物流模式的分析与优化［J］.汽车工程，2011，33(1):79-84.

［2］Witt C.Crossdocking:Concepts Demand Choice［J］.Material Handling Engineering，1998，53(7):44-49.

［3］Kaneko J，Nojiri W.The Logistics of Just-in-Time Between Parts Suppliers and Car Assemblers in Japan［J］.Journal of Transport Geography，2008，16(3):155-173.

［4］Jayaraman V，Ross A.A Simulated Annealing Methodology to Distribution Network Design and Management［J］.European Journal of Operational Research，2003，144(3):629-645.

［5］Ross A，Jayaraman V.An Evaluation of New Heuristics for the Location of Cross-docks Distribution Centers in Supply Chain Network Design［J］.Computers ＆ Industrial Engineering，2008，55(1):64-79.

［6］Bartholdi J J，III，Gue K R.The Best Shape for a Crossdock［J］.Transportation Science，2004，38(2):235-244.

［7］Wen M，Larsen J，Clausen J，et al.Vehicle Routing with Crossdocking［J］.Journal of the Operational Research Society，2008，60(12):1708-1718.

［8］Liao C J，Lin Y，Shih S C.Vehicle Routing with Cross-docking in the Supply Chain［J］.Expert Systems with Applications，2010，37(10):6868-6873.

［9］Oh Y，Hwang H，Cha C N，et al.A Dock-door Assignment Problem for the Korean Mail Distribution Center［J］.Computers ＆ Industrial Engineering，2006，51(2):288-296.

［10］Bozer Y A，Carlo H J.Optimizing Inbound and Outbound Door Assignments in Less-than-truckload Crossdocks［J］.IIE Transactions，2008，40(11):1007-1018.

［11］Mcwilliams D L，Stanfield P M，Geiger C D.The Parcel Hub Scheduling Problem:A Simulation-based Solution Approach［J］.Computers ＆ Industrial Engineering，2005，49(3):393-412.

［12］Yu W，Egbelu P J.Scheduling of Inbound and Outbound Trucks in Cross Docking Systems with Temporary Storage［J］.European Journal of Operational Research，2008，184(1):377-396.

［13］Chen F，Song K.Minimizing Makespan in Two-stage Hybrid Cross Docking Scheduling Problem［J］.Computers＆ Operations Research，2009，36(6):2066-2073.

［14］Chen F，Lee C Y.Minimizing the Makespan in a Two-machine Cross-docking Flow Shop Problem［J］.European Journal of Operational Research，2009，193(1):59-72.

［15］Gue K R.The Effects of Trailer Scheduling on the Layout of Freight Terminals［J］.Transportation Science，1999，33(4):419-428.

［16］Mej A G，Martnez D，Torres F.Modeling and Development of an ARENAⓇInterface for Petri Nets:a Case Study in a Colombian Cosmetics Company［M］.Proceedings of the 40th Conference on Winter Simulation，Miami，Florida;Winter Simulation Conference，2008:1368-1375.

［17］Kleijnen J P C.Design and Analysis of Simulation Experiments［M］.New York:Springer US，2008.

［18］Yaluinkaya O，MiracBayhan G.Modelling and Optimization of Average Travel Time for a Metro Line by Simulation and Response Surface Methodology［J］.European Journal of Operational Research，2009，196(1):225-233.

［19］Su J，Li S，Tadikamalla P.Operational Design of a Supply Chain System Using the Taguchi Method，Response Surface Methodology，Simulation，and Optimization［J］.International Journal of Production Research，2004，42(18):3823-3849.

［20］Noguera J H，Watson E F.Response Surface Analysis of a Multiproduct Batch Processing Facility Using a Simulation Metamodel［J］.International Journal of Production Economics，2006，102(2):333-343.

［21］宋凯，成艾国，钟志华.基于响应面法的汽车车身t型接头优化［J］.汽车工程，2011，33(4):283-289.

［22］田程，桂良进，范子杰.采用序列响应面法的大客车结构振动频率优化［J］.汽车工程，2010，32(10):833-836.