锂离子电池单体热模型研究动态*

宋 丽，魏学哲，戴海峰，孙泽昌

(同济大学汽车学院，新能源汽车工程中心，上海 201804)

前言

锂离子电池具有功率密度和能量密度高、无记忆效应、污染少和所需自然资源丰富等优点，经过20多年的发展，如今已成为新能源电动汽车的储能载体［1-2］。但作为化学电源，锂离子动力电池在充放电时伴随着复杂的化学、电化学反应过程和物质传输过程［3］，这些反应过程中产生的热量和其他因素(电池种类、电池运行工况、冷却方式和电池排列方式等)共同影响电池温度的变化。锂离子电池的特性与其温度有着紧密的关系［4］，温度分布不均匀或温度变化过大等因素会导致电池的早期损坏与热失控，甚至引发安全事故，因此动力用锂离子电池的热管理问题已经成为其车载应用的瓶颈［5］。

电池的热模型是对电池生热、传热和散热的抽象描述，也可分为单体、模块和整包级别。以模型为基础，可分析电池在时间域和空间域上的温度分布，并可解释电池在工作状态下可能出现的热失控现象，从而达到优化电池单体、电池模块和电池包热管理系统的设计以及提高电池使用安全性的目的。

对锂离子电池热模型的研究从20世纪80年代初就已有文献涉及。起初的研究多将锂离子电池假设为均匀的发热源，对电池的平均温度进行分析。文献［6］和文献［7］是较早使用该类模型对锂离子电池热行为进行研究的文章;随着研究的深入，锂离子电池热模型在原有的基础上，考虑了因极耳布置所产生的电流场这一影响因素;锂离子电池多孔电极模型理论［8］提出后，对锂离子电池热模型的研究又逐渐结合了电池内部的物质运输和电化学反应等多物理场因素。在该理论前提下文献［9］中所做的研究比较具有代表性。

现有的对锂离子电池热模型的研究按其建模原理可分为电化学-热耦合模型、电-热耦合模型和热滥用模型;按模型维度可分为集中质量模型、一维模型、二维模型和三维模型。

本文中主要关注正常工作状态下锂离子电池热模型，依照生热率的计算与获取方法将其分为从能量守恒定律角度考虑的均一化热源模型和用锂离子电池内部反应机理公式进行计算的热源分布模型两大类。总结了各锂离子电池热模型的建模方法，重点分析了现今主要的锂离子电池热模型，并指出了现有模型中值得完善的问题，提出了锂离子电池热模型今后的发展方向。

1 热模型基本理论

电池的生热、散热过程是一个典型的有时变内热源的非稳态导热过程［10］，其遵守的能量守恒方程［11-12］为

1.1 生热率的计算

锂离子电池热模型中应用的热量计算公式基本包括3个部分:化学反应产热(由化学反应产生)、浓度差异产热(由物质转移产生)和欧姆产热(带电粒子的焦耳热效应产生)［13-14］。其中焦耳热与浓差极化产热为不可逆热，电化学反应产热为可逆热(又称Peltier热)［15］。

现有的锂离子电池热模型中的热源基本都是基于Bernardi生热率模型［16］。Bernardi生热率为

式中:Ij为电极反应产生的局部反应电流;T∂/∂T为可逆热;为相应的平均开路电压;I为总电流;E为电池电压;为物质反应速率不均匀带来的生热率为相变反应产热率。

式(2)右侧第一项为电化学反应焓，第二项为电池所做的电功，第三项为电池内由于各部分反应速率不一致引起电池内部物质混合不均造成的浓度梯度的产热率，当混合物质的热焓与其浓度的函数关系呈非线性时，这部分热量不可忽略，最后一项为化学反应中由于材料的相变反应产生的生热率。

在正常充放电情况下，可以提出如下假设:当研究对象为厚度方向很薄的电池极片或所研究的电池厚度方向的温差可忽略时，忽略由于副反应带来的电池老化现象，即忽略相变产热;认为模型中电化学系统有很好的传输特性，存在的浓度梯度是可忽略的，即这部分热源可忽略不计，即和可以忽略，故上述热源模型被简化为

文献［17］～文献［20］中在实验的基础上对可逆热源和不可逆热源产热情况进行了分析，见表1。

由表1可以看出，锂离子电池充放电过程中，可逆热与不可逆热基本涵盖了电池产热的绝大部分，qmixing和qphase-change对产热量的贡献较少，使用式(3)作为锂离子电池热模型的热源进行分析，模型的温度情况与实际温度情况的误差在可接受范围之内，不影响对锂离子电池的温度分析。

1.2 传热和散热条件的确定

根据传热学可知热传递方式主要有热传导、对流换热和辐射换热3种。

对于电池内部而言，热辐射和热对流的影响很小，热量的传递主要由热传导决定，其大小与电池内部各部分材料的导热系数有关。在锂离子电池单体热模型中热导率为各向异性，以方形电池单体为例，其热导率为

式中:λx、λy、λz分别为单体电池厚度方向 x和极片平面上的 y、z方向上的热导率;λp、λn、λs、λw分别为电池正极、隔膜、负极、外壳的热导率;Lxp、Lxn、Lxs、Lxw分别为电池正极、隔膜、负极、外壳的厚度;Lx为电池单体厚度。电池内部热传导服从傅立叶定律:

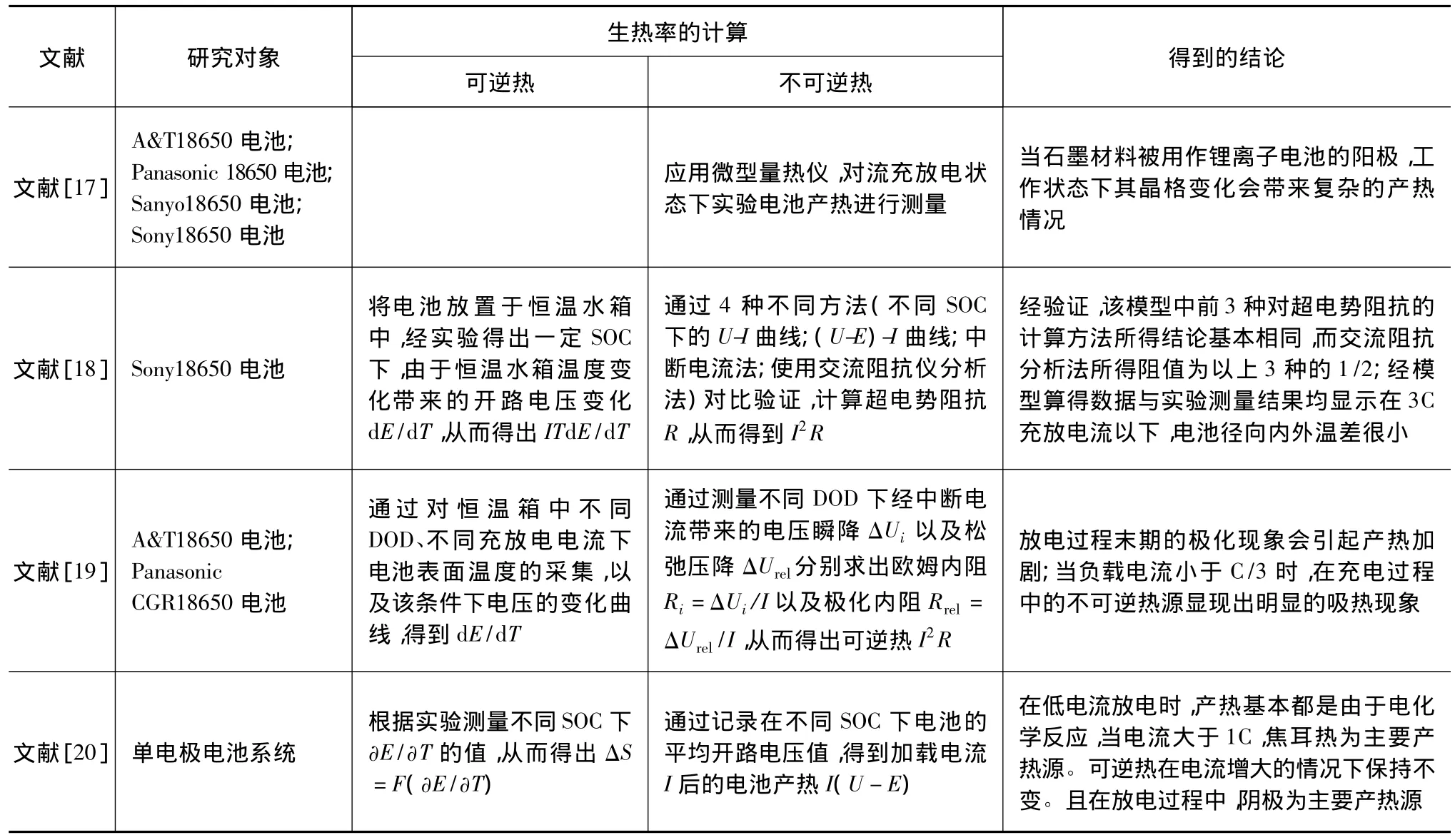
表1 锂离子电池热模型中产热情况研究

式中:qn为热流密度;λk为导热系数;∂T/∂n为电极等温面法线方向温度梯度。

电池表面的热量传递主要由热对流所决定，主要与冷却环境(对流换热系数、环境温度)有关。计算热流量Q的牛顿公式为

式中:h为对流换热系数;F为电池表面与环境之间的接触面积;ΔT为电池表面温度与流体温度之差。该项一般作为电池热模型求解的边界冷却条件。

2 锂离子电池热模型的分类

在锂离子电池总体发热量得到定量保证的前提下，研究人员从两种不同的思路出发建立了锂离子电池热模型:

(1)均一化参数模型 将锂离子电池的热源设置成某一均匀发热的区域，例如电池内某一点、某一截面或某一块体积，通过材料的导热特性换算成温度输出;

(2)分布参数模型 考虑锂离子电池内发热体的不均匀性，对电池内部的温度分布情况进行精确求解。

2.1 均一化参数模型

在式(3)热源计算公式的基础上，一部分研究以发热量、电池总体温升和温差大小以及不同散热系数的影响为主题，建立了均一化热源的电池热模型，此类热模型认为电池充放电时，电池内核区域各处电流密度均匀，生热率一致。模型求解时电池单元的比热和热导率一般都以加权平均值计算。

文献［21］中对SONYUS 18650 G3小型锂离子圆柱电池建立了二维和三维模型，利用该模型在实验数据的基础上分别计算出了电池在不同条件下放电过程的可逆热源和不可逆热源的产热量。如图1所示，图中左侧圆点区域为产热区，右侧灰色区域为求解域。该模型中的热源均匀分布在产热区，使用二维模型分析了电池经1.8A恒流放电后中间纵截面的温度分布，与实验测量数据相差0.6K，能较为精确地仿真出圆柱形电池的温度分布情况。

文献［22］中对磷酸铁锂26650圆柱电池建立了类似于等效电路的等效热模型，见图2。图中，Q·为电流源;Rin为电池等效热阻;Rout为电池与环境之间的等效热阻;Cp为电池等效热容;Tamb为体积内空气温度;Tsurf为热电偶实测电池表面温度;Tin为电池内部温度。

该等效电路模型中电容和电阻用来表示热量积累和传导现象，电流源用来表示发热源。模型内部温度的估计值为

文献中将估计的电池内部温度与实测温度做了对比，差异在1.5℃之内。由于该模型计算非常简单，又能保证一定的精度，使实现电源管理系统(battery manage system，BMS)在线估计的可能性较高，因此具有较高的参考价值。

综上可见，圆柱形电池由于其单元电池卷绕的特点，热源的分布情况不明显，所以在使用均一化热源的模型结构进行仿真时可以保证较高的模型精度，计算也比较简单，有在线估计的可能性。

文献［23］中应用有限元的分析方法，在锂离子电池传热的数学模型基础上，建立了锰酸锂电池的三维不分层模型，对该电池的热物理性能进行了研究。根据实验数据得到了总产热量，并在假设电池的生热率和电池材料为对称的前提下，对电池1/8模型进行了传热分析，得到了该电池在不同换热系数和不同工况点的温度分布云图，并且提出了一些电池热管理方案的建议。

类似的研究还有文献［24］中对 NEC MP-5A 260948电池的建模、文献［25］中从电池单元出发，对100A·h锰酸锂电池建立的三维电池热模型、文献［26］中应用有限元法对某55A·h的磷酸铁锂电池建立的1/2模型、文献［27］中建立的简化锂离子电池热模型等。

该类模型忽略了电流密度分布对电池温度场的影响，将锂离子电池简化为不分层结构求解可在一定程度上减少计算量，可较精确地仿真出方形电池最高温度和最低温度的温升及其温差，以及电池整体的平均温度。另外，从材料出发计算均一化热容、热阻的方法有效避免了将电池作为黑匣子的热力学测试过程，对于实际工程应用有比较重要的指导意义，但对于方形电池内部温度分布的模拟结果与实际情况差异较大。

2.2 分布参数模型

该类模型可用于模拟不同工况下，电池整体温度随时间的变化情况和在某时刻电池某截面上电流密度分布、温度分布等。模型仿真结果可用以指导电池材料、尺寸、极耳布置等的选择和设计，且有助于研究电池的一致性和寿命等问题。

这类模型在生热率的计算中考虑了局部电流的分布所带来的部分焦耳热，应用有限元或有限体积法，对电池单体的温度场分布进行研究。基于电流密度的生热率和电流密度J计算公式为

式中:φs、φe分别为固相以及液相中的电势;σeff为固相颗粒的电导率;κeff为电化学反应速率常数;κeffD为液相离子电导率;ce为电解质浓度;cs，max为固相中插入锂离子的最大浓度;cs，surf为固相表面锂离子浓度;F为法拉第常数;R为气体常数;η为电化学反应超电势。

式(9)等号右侧第一项为总反应热与可逆热生热率的和，第二项为电极中固相颗粒欧姆反应生热率，后两项为电极中液相成分欧姆反应生热率。

文献［28］中应用有限元计算方法，分别对10和26A·h聚合物锂离子电池的单电极单元(正极片+负极片)建立了二维简化模型，通过电荷守恒定律来描述两极片之间的物质输送关系，见图3。通过红外热像仪对电池温度场进行拍摄来验证模型的准确性，见图4。

由于该二维简化模型忽略了电池厚度方向的传热，导致了模型中最低温度点模拟结果不准确。此外，文献［29］中还应用此方法对14.6A·h的锰酸锂电池在充电过程中的温度场的分布进行了分析。研究均从实验和仿真两方面反映了电流密度分布对于电池内部温度分布的重要影响，电池内部特性逐渐成为电池热模型不可忽略的重要因素。

在上述研究的基础之上，文献［30］中应用同样的方法分析了不同极片尺寸和不同极耳位置的聚合物锂离子电池的单电极单元在不同放电电流下的电压、电流密度和温度的分布情况。优化了极片和极耳的设计方案。

随着对电池内部机理进一步的深入研究，影响电流密度分布的众多耦合因素被逐渐加入热模型中，模型趋向复杂。

文献［9］中应用有限体积计算法对锂离子电池建立了多维模型。该模型在粒子域以及电极域内参考了锂离子电池单极片二维扩散模型。图5为多维模型中相邻维度模型之间的变量耦合情况:高维度中的参数(点电势φ、温度T等)以场量形式输入低维度中(被视为高维度参数的集中平均值，即其在低维中没有空间坐标依赖性);低维度中的参数(电流i、产热q等分布参数)以体积源的方式输入高维度中(在低维度上进行平均以消除其坐标依赖性)。该种方法大大简化了分布参数模型的计算量，并且将粒子机理模型与极片模型分别封装起来，简化了模型的更新和对于特定参数的分析。

近几年还出现了一批锂离子电池的分布参数热模型，例如为钴酸锂软包电池建立的电化学-热耦合模型［31］;为锰酸锂圆柱形锂离子电池建立的电化学-热耦合模型［32］，并对其热特性进行了研究;使用基于有限元法的comsol多物理场耦合软件，在已发布的锂离子电池模型基础上，耦合了焦耳热场［33］等等。

这类模型(分布参数模型)基本上都是从多孔电极理论模型［8］出发，重点考虑了极片上的电流分布对于温度的影响，从图4中的对比温度分布可以看出，该类模型能够精确描述电池内部温度的分布，相对于均一化热源电池热模型计算出来的“鸡蛋形”温度分布有着非常重要的实际意义，在电池设计、电池冷却和电池内部不一致性等问题上都是一个强有力的分析手段。但该类模型计算量大，计算方法复杂，分析时间长，同时模型的建立与精确度强烈依赖于对正负极材料体系的研究程度，所以迄今还没有非常精确的关于磷酸铁锂正极材料体系锂离子电池的机理模型和分布热源模型。

随着各种参数基础研究的深入，人们越来越清晰地认识到电池各项参数之间复杂的耦合关系。任何仅仅研究电池某一方面性能的模型都是不够的。文献［34］在comsol软件中的锂离子电化学模型的基础上，对11.5A·h的锰酸锂电池建立了基于电化学-热耦合的综合模型，以分布参数热模型为平台，考虑温度变化对电池性能的影响进行修正，并反馈到发热量的计算，综合考虑了电池内部的复杂耦合关系，是对综合模型的一个较好的示例和阐释。

3 总结与展望

对锂离子电池热模型研究的基本走向为以下两个不同的方向。

(1)从外特性出发，计算或者测量电池的总发热量，通过不同的方法获得电池的热阻和热容参数，进而仿真得到电池平均温升、内外温差和发热量变化规律。此类模型可较准确地模拟出电池温升和温差的大小，对于电池的传热散热方案有一定的指导意义，同时计算较为简单，工程化实现的可能性较高，但是这类研究方法是基于热源均匀发热的假设，对于电池内部温度的分布和电池内部温度与电流不一致性的影响未予考虑，故不能指导电池的具体设计。

(2)从电池电化学反应与内部电流分布机理出发，研究不同时刻电池内部的电流密度和温度等分布参数。该类模型较为精确地估计了电池内部的温度变化情况，对于研究电池的实际热分布与温度分布有着十分重要的意义，同时该类模型对于指导改进电池的材料物性、电池的形状尺寸、极耳布置设计等具有重大的参考价值，另一方面，通过温度因子将电池反应机理和老化机理进行耦合，也可研究电池在内部温度与电流不一致的情况下的响应和对寿命等的影响。

将来的锂离子电池热模型仍然会朝着这两个方向发展:在外特性方面，参考机理模型对于电池热现象的解释，优化和修正均一化模型结构，着重于简单准确的在线算法，更加方便在BMS中集成对温度的辨识和管理能力，这类问题通常利用MATLAB、C、FORTRAN等编程平台来实现;在分布参数热模型中，进一步详细模型细节，结合电池单体内部的电流密度分布情况，研究电池单体温度场的分布，指导改进电池外型、极耳、材料等的选择与设计，同时可帮助研究电池的一致性和安全性问题。尤其是现今的分布参数热模型大多向着多尺度、多维度的方向完善，这类模型大多依托于大型有限元分析软件充分考虑电流场、热场和电化学等多种物理场之间的复杂耦合关系，采用基于完全非结构化网格的有限体积法(如FLUENT)或通过迭代收敛求解偏微分方程组(如COMSOL Multiphysics)等进行求解，更好地将锂离子电池内部微观机理反映到实际的工程实践中，对于电池结构的设计和热管理方案的制定将会起到不可或缺的作用。

［1］Morita M，Kawasaki T，Yoshimoto N，et al.Nonflammable Organic Electrolyte Solution Based on Perfluoro-ether Solvent for Lithium ion Batteries［J］.Journal of the Electrochemical Society，2003，71:1067-1069.

［2］Capiglia C，Yang J，Imanishi N，et al.DSC Study on the Thermal Stability of Solid Polymer Electrolyte Cells［J］.Journal of Power Sources，2003，119-121:826-832.

［3］Selman J R，Hallaj S A，Uchida I，et al.Cooperative Research on Safety Fundamentals of Lithium Batteries［J］.Journal of Power Sources，2001，97-98:726-732.

［4］Pesaran A A.Battery Thermal Models for Hybrid Vehicle Simulations［J］.Journal of Power Sources，2002，110(2):377-382.

［5］Alvani-Soltani S R，Ravigururajan T S，Rezac M.Proceedings of IMECE，2006［C］.American Society of Mechanical Engineers:383.

［6］Botte G G，Johnson B A，White R E.Influence of Some Design Variables on the Thermal Behavior of a Lithium-ion Cell［J］.Journal of Electrochemical Society，1999，146:3.

［7］Sato N.Thermal Behavior Analy Sis of Lithium-ion Batteries for E-lectric and Hybrid Vehicles［J］.Journal of Power Sources，2001，99:70-77.

［8］Doyle M，Newman J.Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells［J］.Journal of the Electrocchemical Society，1996，143:1890-1903.

［9］Kim Gi-Heon，Smith Kandler，Lee Kyu-Jin，et al.Multi-domain Modeling of Lithium-ion Batteries Encompassing Multi-physics in Varied Length Scales［J］.Journal of the Electrochemical Society，2011，158:A955-A969.

［10］Pesaran A，Vlahinos A，Bharathan D.National Renewable Energy Laboratory，Electrothermal Analysis of Lithium Ion Batteries，NREL/AB-540-39502［R］.2006，12.

［11］Lee J.Electrochemical and Thermal Modeling of Battery，Fuel Cell，and Photo Energy Conversion Systems［C］.The Electrochemical Society Proceedings Series，Pennington，NJ，1986.

［12］Newman J，Tiedemann W.Temperature Rise in a Battery Module with Constant Heat Generation［J］.Journal of the Electrochemical Society，1995，142:1054-1057.

［13］Gu W B，Wang C Y.Thermal-Electrochemical Modeling of Battery Systems［J］.Journal of Electrochemical Society，2000，147:2910-2922.

［14］Kumaresan K，Sikha G，White R E.Thermal Model for a Li-ion Cell［J］.Journal of Electrochemical Society，2008，155:A164-A171.

［15］Yokoyama K，Fujita S，Hiwara A，et al.Non-aqueous Electrolytic Solutions and Non-aqueous Electrolyte Cells Comprising the Same:U.S.，5580684［P］.1996-12-03.

［16］Bernardi D，Pawlikowski E，Newman J.A General Energy Balance for Battery Systems［J］.Journal of Electrochemical Society，1985，132:1.

［17］Saito Y，Takano K，Kanari K，et al.Comparative Study of Thermal Behaviors of Various Lithium-ion Cells［J］.Journal of Power Sources，2001，97-98:688-692.

［18］Onda K，Ohshima T，Nakayama M，et al.Thermal Behavior of Small Lithium-ion Battery During Rapid Charge and Discharge Cycles［J］.Journal of Power Sources，2006，158:535-542.

［19］Hallaj S AL，Prakash J，Selman J R.Characterization of Com-mercial Li-ion Batteries Using Electrochemical-calorimetric Measurements［J］.Journal of Power Sources，2000，87:186-194.

［20］Lu Wenquan，Yang Hui，Prakash Jai.Determination of the Reversible and Irreversible Heats of LiNi0.8Co0.2O2/Mesocarbon Microbead Li-ion Cell Reactions Using Isothermal Microcalorimetery［J］.Electrochimica Acta，2006，51:1322-1329.

［21］Inui Y，Kobayashi Y，Watanabe Y，et al.Simulation of Temperature Distribution in Cylindrical and Prismatic Lithium Ion Secondary Batteries［J］.Energy Conversion and Management，2007，48:2103-2109.

［22］Christophe Forgez，Dinh Vinh Do，Guy Friedrich，et al.Thermal Modeling of a Cylindrical LiFePO4/Graphite Lithium-ion Battery［J］.Journal of Power Sources，2010，195:2961-2968.

［23］Lin Cheng，Chen Ke，Sun Fengchun，et al.Research on Thermo-physical Properties Identification and Thermal Analysis of EV Li-ion Battery［C］.Vehicle Power and Propulsion Conference，2009.

［24］Kobayashi Y，Kihira N，Takei K，et al.Electrochemical and Calorimetric Approach to Spinel Lithium Manganese Oxide［J］.Journal of Power Sources，1999，81-82:463-466.

［25］林成涛，李腾，陈全世.锰酸锂动力蓄电池散热影响因素分析［J］.兵工学报，2010，31(1):88-93.

［26］Gui Fang Guo，Bo Long，Bo Cheng，et al.Three-dimensional Thermal Finite Element Modeling of Lithium-ion Battery in Thermal Abuse Application［J］.Journal of Power Sources，2010，195:2393-2398.

［27］Chen S C，Wan C C，Wang Y Y.Thermal Analysis of Lithiumion Batteries［J］.Journal of Power Sources，2005，140:111-124.

［28］Kim Ui-seong，Shin Chee-burm，Kim Chi-su.Modeling for the Scale-up of a Lithium-ion Polymer Battery［J］.Journal of Power Sources，2009，189:841-846.

［29］Kim Ui-seong，Yi Jaeshin，Shin Chee-burm，et al.Modelling the Thermal Behaviour of a Lithium-ion Battery During Charge［J］.Journal of Power Sources，2011，196:5115-5121.

［30］Kim Ui-seong，Shin Chee-burm，Kim Chi-su.Effect of Electrode Configuration on the Thermal Behavior of a Lithium-polymer Battery［J］.Journal of Power Sources，2008，180:909-916.

［31］Kumaresan K，Sikha G，White R E.Thermal Model for a Li-ion Cell［J］.Journal of The Electrochemical Society，2008，155(2):A164-A171.

［32］Zhang Xiongwen.Thermal Analysis of a Cylindrical Lithium-ion Battery［J］.Electrochimica Acta，2011，56:1246-1255.

［33］Cai Long，White R E.Mathematical Modeling of a Lithium Ion Battery with Thermal Effects in COMSOL Inc.Multiphysics(MP)Software［J］.Journal of Power Sources，2011，196:5985-5989.

［34］Ye Yonghuang，Shi Yixiang，Cai Ningsheng，et al.Electro-thermal Modeling and Experimental Validation for Lithium Ion Battery［J］.Journal of Power Sources，2012，199:227-238.