3种确定性采样非线性滤波算法的复杂度分析

张召友，郝燕玲，吴 旭

(哈尔滨工程大学自动化学院，150001哈尔滨)

卡尔曼滤波是实现捷联惯性导航系统(strapdown inertial navigation system，SINS)和全球定位系统(global positioning system，GPS)组合导航数据融合的首选方法［1-2］.低精度传感器构成的组合系统在复杂应用环境中易产生大的误差，导致系统非线性度增加，此时线性卡尔曼滤波已不再适用，而扩展卡尔曼滤波(extended Kalman filter，EKF)也难以保证系统性能.随着近年非线性滤波的快速发展，较EKF精度更高的确定性采样卡尔曼滤波被用于处理组合导航中的非线性融合问题.确定性采样卡尔曼滤波是一类利用有限固定采样点对高斯系统中状态的一二阶矩进行近似，并经过非线性函数传播后进行加权求和估计的滤波算法.最为常用的3种确定性采样算法为［3］无迹卡尔曼滤波(unscented Kalman filter，UKF)、中心差分卡尔曼滤波(central difference Kalman filter，CDKF)、容积卡尔曼滤波(cubature Kalman filter，CKF)算法.

精度是表征滤波性能的重要指标，大量文献已证实UKF、CDKF、CKF的精度相当，均至少可达二阶［4-5］.但在导航系统中，滤波多是在嵌入式计算机中实现，因此复杂度是影响其应用的另一个重要参数.先前对于非线性滤波复杂度的研究多是对单一算法的改进与分析［6-8］，对于形式相近的确定性采样算法之间缺乏系统的分析与比较.因此，本文将对3种典型确定性采样算法进行等效复杂度的理论分析，导出定量的计算表达式，并进行横向比较，得出算法实时性选择的依据.最后，将确定性采样算法应用于SINS/GPS的紧耦合组合导航，对其精度和复杂度进行仿真，验证分析的正确性.

1 确定性采样滤波的等效复杂度分析

滤波的精度是保证系统性能的前提，但当精度满足要求后滤波的易实现性与否是另一个制约因素，复杂度是表征易实现性的主要参数.本节将对UKF、CDKF、CKF的复杂度及差异进行分析，力图得出一个精确的、定量的表述.

1.1 确定性采样滤波中数值运算的复杂度

分析算法复杂度最为有效的方法是对其浮点操作数(flops)的准确统计.一次flops定义为两个浮点数进行一次加、减、乘或除法运算.但滤波中的很多运算难以用加、减、乘、除来简单描述，如开方、数值分解、指数运算等，因此只能将其等效为相同运行时间的flops，故称为等效复杂度分析.本文给出滤波中基本代数运算的flops次数［1］:1)矩阵加减法.A∈Rn×m，B∈Rn×m，计算A±B需nm次flops.2)矩阵相乘.A∈Rn×m，B∈Rm×l，计算AB的flops为2mnl-nl次.3)矩阵求逆.A∈Rn×n，A-1的flops数为n3.4)Cholesky分解.A∈Rn×n，则chol(A)需要进行n3次flops.

利用上述诸元素即可对确定性采样卡尔曼滤波进行复杂度的分析.

1.2 确定性采样滤波的等效复杂度分析

3种确定性采样算法的滤波形式相近，均包括样本点产生、基于状态方程与量测方程的均值与方差预测以及状态与方差的后验估计等步骤.算法实现形式均为加性噪声形式，UKF与CDKF的详细公式参见文献［4］，CKF的公式参见文献［5］.按照滤波过程可对相应算法进行分析.由于具体的分析过程较为繁琐，在此只给出CKF算法的分析过程如下.

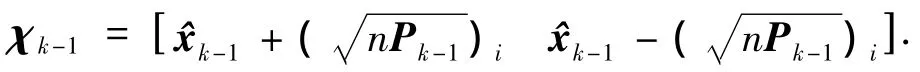
状态方程预测，如下式，获得样本点预测χk｜k-1需要4n3-2n2次flops(3种算法均以线性矩阵形式代换)，获得状态预测值1需要2n2次flops，预测协方差Pk｜k-1需要 2n3+4n2次 flops.

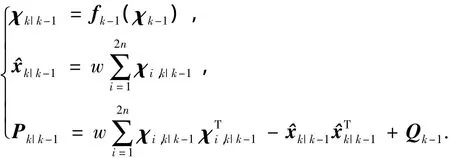
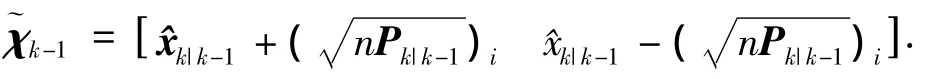
量测方程预测，如下式，获得样本点预测γk｜k-1需要 4n2l-2nl次 flops，获得量测预测值yk｜k-1需要2nl次flops，预测量测协方差Pyk需要4nl2+3l2次flops，互协方差Pxkyk需要4n2l+2nl次flops.

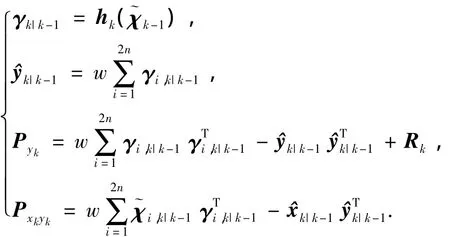
计算后验估计，如下式，增益Kk需l3+(2nl2-nl)次flops，协方差更新Pk需要2nl2-nl+2n2l次flops，状态更新需要2nl+l次flops.

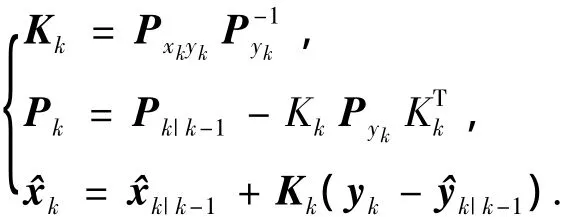
总结以上分析，CKF的复杂度fCKF总计为

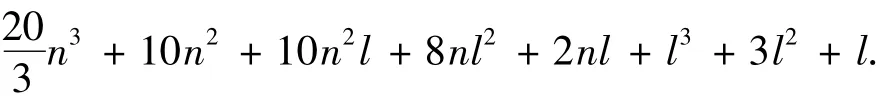
同理，可对UKF和CDKF进行分析，滤波参数的具体分析结果如表1所示.由表中数据可计算得到UKF的复杂度fUKF总计为

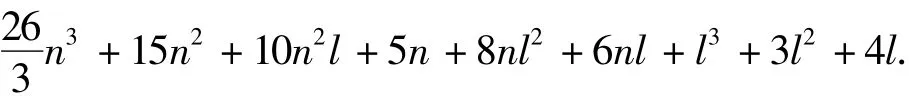
CDKF的复杂度fCDKF总计为

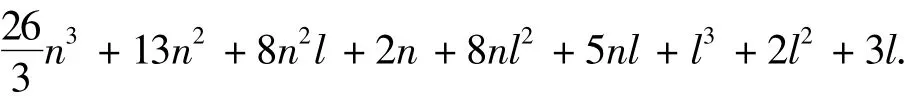
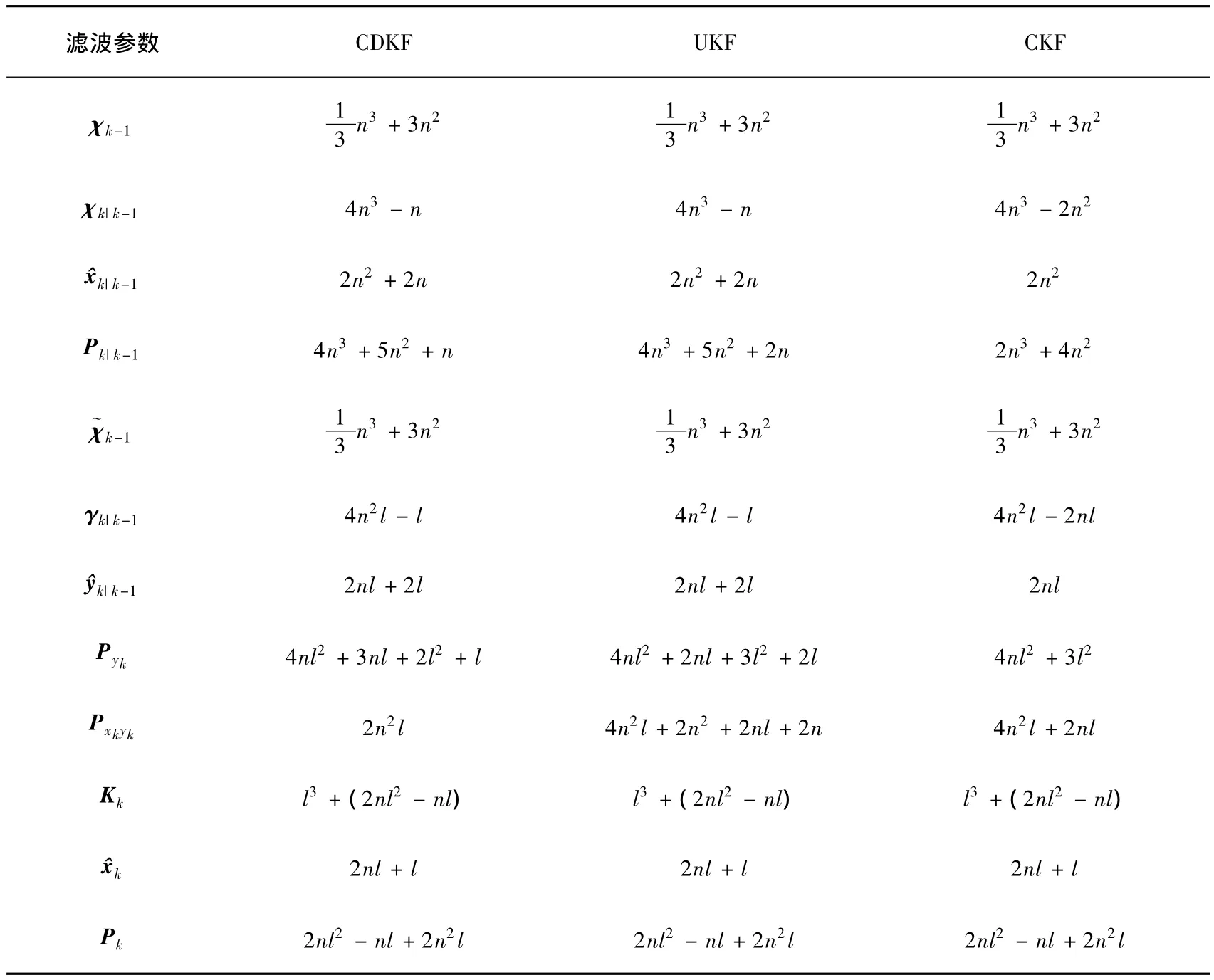
表1 确定性采样卡尔曼滤波复杂度分析结果

由3个表达式可看出，CDKF、UKF、CKF 3种算法的复杂度均为O(n3)和O(l3)量级，即与状态维数和量测维数均呈三次方关系.

通过对3种算法总体复杂度系数项的直观比较可知:fUKF＞fCDKF和fUKF＞fCKF恒成立，即UKF的复杂度始终最高.而CDKF和CKF的复杂度难以通过系数项直接看出，所以将两者求差得

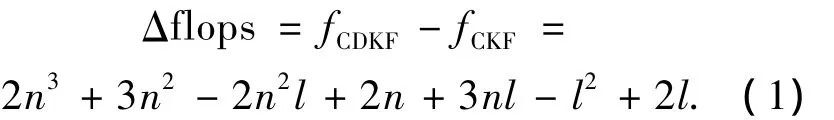
式(1)仍为状态维数n的三次方形式，不便于分析.假设状态维数n和量测维数l存在n-l=k的关系，其中k为整数，则式(1)可分别整理为关于n和l的二次项形式，即

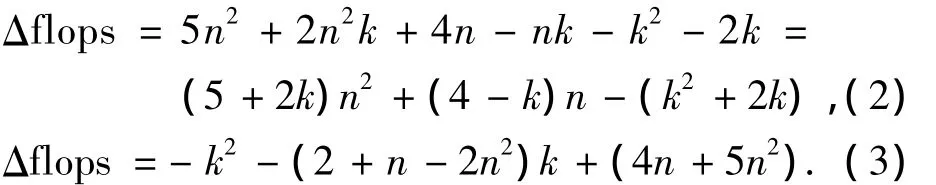
当0≤k＜n时，状态维数大于量测维数，由式(2)可知Δflops为关于n的开口向上的抛物线，且n=1时Δflops＞0，所以Δflops为状态维数n的单增函数，即状态维数大于量测维数时，fCDKF＞fCKF恒成立，且随着状态维数增大，CDKF与CKF的差异也增大.

当k≤0时，量测维数大于状态维数，由式(3)知Δflops为关于k的开口向下的抛物线，所以随着k的不断减小，会出现Δflops＜0的情况，即量测维数与状态维数差异的不断加大，CKF的复杂度会高于CDKF，即fCKF＞fCDKF.具体差异可根据实际系统的维数及前面的复杂度计算式进行计算得出.

为更为直观的揭示三者之间的差异，根据复杂度计算式绘出了图1、2所示的状态和量测维数分别变化时3种算法复杂度的变化曲线.

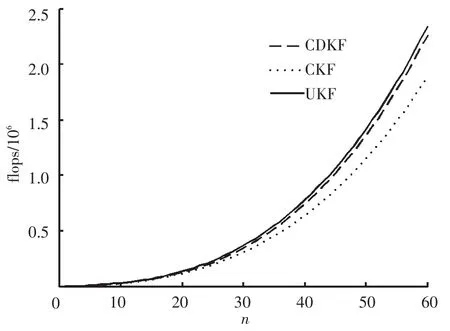
图1 确定性采样卡尔曼滤波复杂度(l=10)

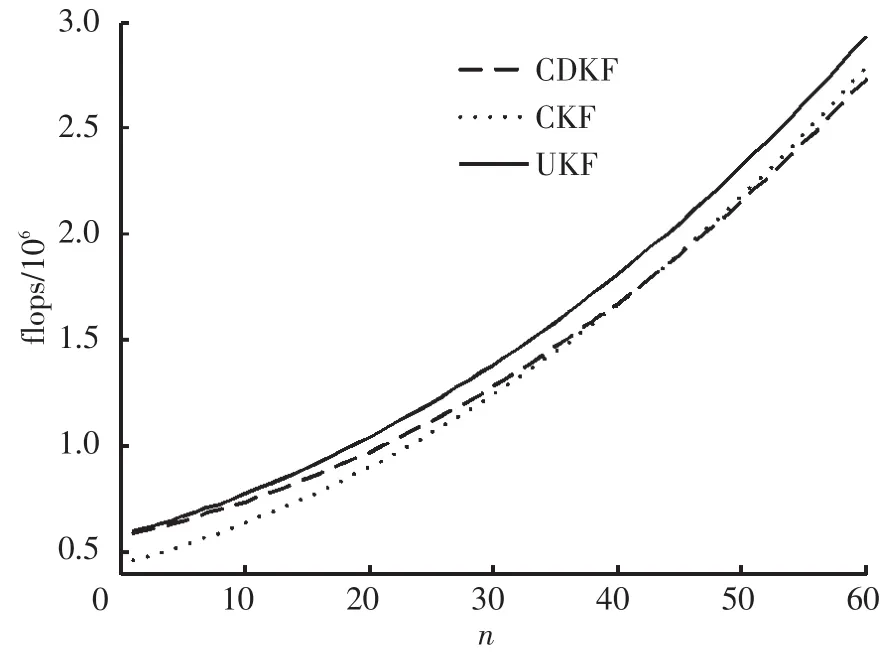
图2 确定性采样卡尔曼滤波复杂度(n=40)

2 仿真实验与分析

为验证UKF、CDKF和CKF算法复杂度分析的正确性及在精度上的一致性，分别将其应用于SINS/GPS的紧耦合导航中.

状态方程选取大方位失准欧拉角非线性模型，具体见文献［9］，状态量为:x=［δψ，δθ，δγ，δVE，δVN，δVU，δL，δλ，δh，εx，εy，εz，▽x，▽y，▽z，bt，dt］T.其中，(δψ，δθ，δγ)为姿态误差，(δVE，δVN，δVU)为速度误差，(δL，δλ，δh)为位置误差，ε和▽分别为陀螺和加速度计常值漂移，bt和dt分别为时钟偏置和漂移.

利用4颗卫星的伪距与伪距率作为观测量，则卫星i的量测值为yi，k=［ρi，k，ρi，k］，ρi，k为伪距，ρi，k为伪距率.具体非线性量测方程参见文献［10］.

综上可知，状态维数为n=17，量测维数为l=8.根据前面对复杂度的分析，l=8时有fUKF＞fCDKF＞fCKF.

仿真中载体分别经过静止、加速、爬升等阶段.初始位置为(126.67°，45.78°，100 m).初始失准角为(5°，5°，20°).SINS传感器各参数为:陀螺常值漂移100°/h，随机漂移0.3°/;加速度计零偏0.001g(g=9.780 3 m/s2)，随机噪声伪距率量测噪声为0.1 m/s;伪距量测噪声为10 m;时钟偏差为100 m;时钟漂移噪声为0.1 m/s.

随机产生20组数据进行蒙特卡罗仿真.图3、4分别给出了紧耦合的姿态和位置估计误差曲线(20次仿真平均值).表2给出了确定性采样滤波在SINS/GPS紧耦合导航中的估计精度(20组均方跟误差的平均值).由图3、4可知，基于确定性采样原理的UKF、CDKF、CKF 3种算法均可使姿态和位置快速收敛，并且精度相近，只有可忽略的轻微不同.UKF、CDKF、CKF 3种算法的单次导航迭代耗时(20次仿真平均值)分别为7.23、6.92、6.74 ms.可见，UKF的复杂度最高，CDKF次之，CKF最低，与理论分析结果一致.

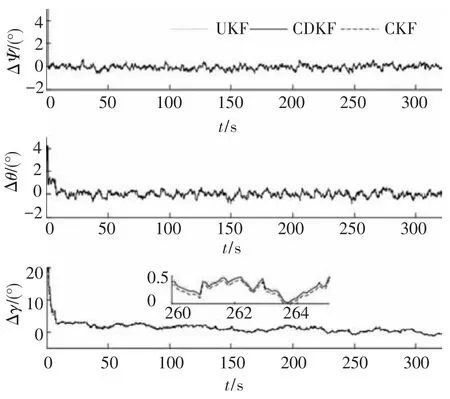
图3 载体姿态误差

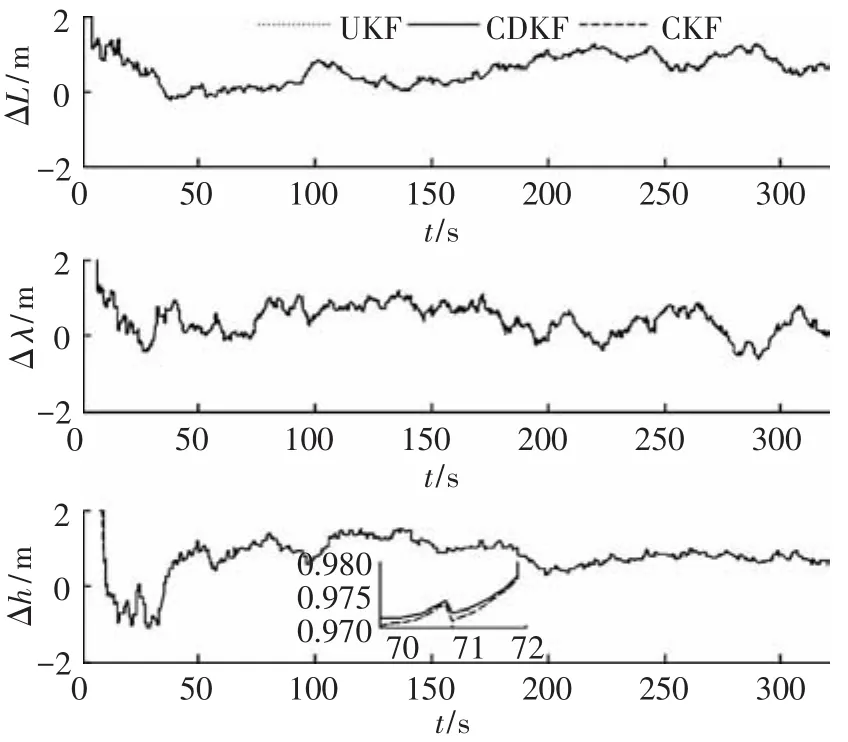
图4 载体位置误差

表2 SINS/GPS紧耦合导航估计性能

3 结论

1)针对确定性采样非线性滤波的实时性问题，对UKF、CDKF和CKF 3种常用算法进行了复杂度分析，导出了复杂度计算的表达式.

2)通过进一步的差异性比较，表明3种算法中UKF复杂度最高;当状态维数高于量测维数时，CDKF的复杂度低于UKF的复杂度，CKF的复杂度最低;量测维数相对状态维数较高时，CDKF的复杂度会低于CKF的复杂度，在诸如雷达测距［11］等高维量测系统中选取CDKF可获得最小的硬件开销.

3)将3种算法应用于SINS/GPS的紧耦合导航中，仿真结果表明了分析结果的正确性.

［1］GREWAL M S，ANDREW A P.Kalman filtering，theory and practice using Matlab［M］.2nd ed.New York:John Wiley＆Sons，2008:225-289.

［2］姬晓琴，高晓颖.低轨卫星紧组合导航UKF方法［J］.哈尔滨工业大学学报，2012:44(7):135-138.

［3］王小旭，潘泉，黄鹤，等.非线性系统确定采样型滤波算法综述［J］.控制与决策，2012，27(6):801-812.

［4］MERWE R V D.Sigma-point Kalman filter for probabilistic inference in dynamic state-space models［D］.Portland:Oregon Health＆Science University，2004:108-110.

［5］ARASARATNAM I，HAYKIN S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control，2009，54(6):1254-1269.

［6］赵恒，苏永清，叶萍.快速传递对准滤波器设计及其计算复杂度分析［J］.弹箭与制导学报，2011，31(3):31-34.

［7］HOLMES S A，KLEIN G，MURRAY D W.An O(N2)square root unscented Kalman filter for visual simultaneous localization and mapping［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31(7):1251-1263.

［8］KARLSSONR，SCHONT，GUSTAFSSONF.Complexity analysis of the marginalized particle filter［J］.IEEE Transactions on Signal Processing，2005，53(11):4408-4411.

［9］ALI J，MIRZA M.Performance comparison among some nonlinear filters for a low cost SINS/GPS integrated solution［J］.Nonlinear Dynamics，2010，61(3):491-502.

［10］LI Y，RIZOS C，WANG J，et al.Sigma-point Kalman filtering for tightly coupled GPS/INS integration［J］.Journal of the Institute of Navigation，2008，55(3):167-177.

［11］MCMANUS C，BARFOOT T.A serial approach to handling high-dimensional measurements in the sigmapoint Kalman filter［C］//Proceedings of Robotics Science and Systems.Los Angeles，CA:MIT Press，2011.