影响双向张弦梁结构受力性能的参数分析

吴 捷

(1.苏州大学金螳螂建筑与城市环境学院，215000江苏苏州;2.东南大学土木工程学院，210096南京)

双向张弦梁作为一种新型的张弦梁结构体系，弥补了单向张弦梁侧向稳定不足，以及仅平面内传力造成的传力效率低等缺点，并成功应用于2008年北京奥运会主体育馆屋盖受力体系.以往普遍的观点是双向张弦梁结构与单向张弦梁结构的性能类似，但随着研究的深入，双向张弦梁的自身特点和特殊性能逐渐凸显［1-4］.作为一类典型的空间受力体系，影响双向张弦梁结构受力性能和优化设计的主要参数与单向或单榀张弦梁相比而言要复杂很多，包括了结构的高跨比(结构上弦最大高度与短跨长度之比)、垂跨比(结构下弦最大垂度与短跨长度之比)、间距比(结构两个方向张弦梁的间距之比)、长宽比(结构两个方向的总跨度之比)以及影响预应力取值的平衡荷载值的大小等.本文将运用基于平衡荷载态的双向张弦梁优化设计的基本思路和方法对各参数的优化进行详细分析.

1 参数优化分析的力学模型

本文选取的基准模型为某购物中心48 m×48 m跨度的双向张弦梁屋盖结构，如图1所示.结构平面均匀分为8×8格，横向(x向)和纵向(y向)均布置7道索和梁，已知上弦梁系为双向抛物面，抛物面曲面方程为z(x，y)=1.6×周边在一平面上，抛物面最高点处梁高1 600 mm，下弦跨中垂度为2 000 mm.上弦各节点作用的竖向最大荷载为63 kN，最小竖向荷载为36 kN.只改变一种结构参数，分析其对双向张弦梁以结构用钢量最小为目标的优化结果的影响.

优化结果通过两步3级优化算法得到.第1步，基于结构在平衡荷载态下的泊松方程进行结构上弦梁拱和下弦索网形状的优化并确定初始预应力的分布，即通过索网形状优化确定各撑杆高度平面分布形式，根据确定后的索网曲面形状以及平衡荷载态下的索力水平分量，通过预应力与几何的联合找形，最终确定各榀索的初始预应力，该方法的正确性已在文献［5-6］中进行了详细的阐述和验证;第2步，结合零阶与一阶优化算法进行杆件截面尺寸的优化［7-10］.其中第2步优化按照索截面、上弦梁杆截面和撑杆截面3个等级依次进行.

这里所提及的平衡荷载指的是假设上弦钢梁为平面时，由索网提供并经撑杆底部传递给上弦每个节点的竖直向上的节点力.当上弦为曲面时，平衡荷载是上弦钢梁和下弦索网在节点处的竖向合力.当结构受到竖向向下的外荷载等于这个平衡荷载值时，上弦刚性梁几乎不受弯，整个结构处于荷载阶段受力最佳时刻.经分析发现，当双向张弦梁结构所受竖向荷载最小值小于结构自重时，平衡荷载值应取为竖向荷载最小值与最大值之间的平均值;当双向张弦梁结构所受竖向荷载最小值大于结构自重时，平衡荷载值应取为结构自重与竖向最大值的平均值［10］.在以结构自重最轻为优化目标的结构优化设计过程中，由于结构的自重是未知量，是优化设计的目标值，因此可以近似取平衡荷载值为结构所受竖向荷载最小值和最大值的平均值.本文的基准模型近似取45 kN为平衡荷载值.

选取箱形截面上弦梁及边梁初始尺寸为600 mm×300 mm×15 mm×8 mm，下弦索初始截面为1 080 mm2，撑杆初始截面为1 103 mm2，屋面柔性支撑初始截面为113 mm2，梁杆的许用应力为［σ］=310 N/mm2，索的许用应力为［σ］=850 N/mm2，最大允许竖向位移L/300，压杆长细比上限［λ］=150.梁截面宽度为200～1 000 mm，高度为300～1 000 mm，梁宽侧面厚度为2～25 mm，梁高侧面厚度为6～25 mm.撑杆截面积为200～4 000 mm2，柔性支撑截面积为20～3 000 mm2.本文仅考虑同方向的上弦梁、所有边梁、撑杆、柔性支撑分别选择统一型号的截面尺寸.

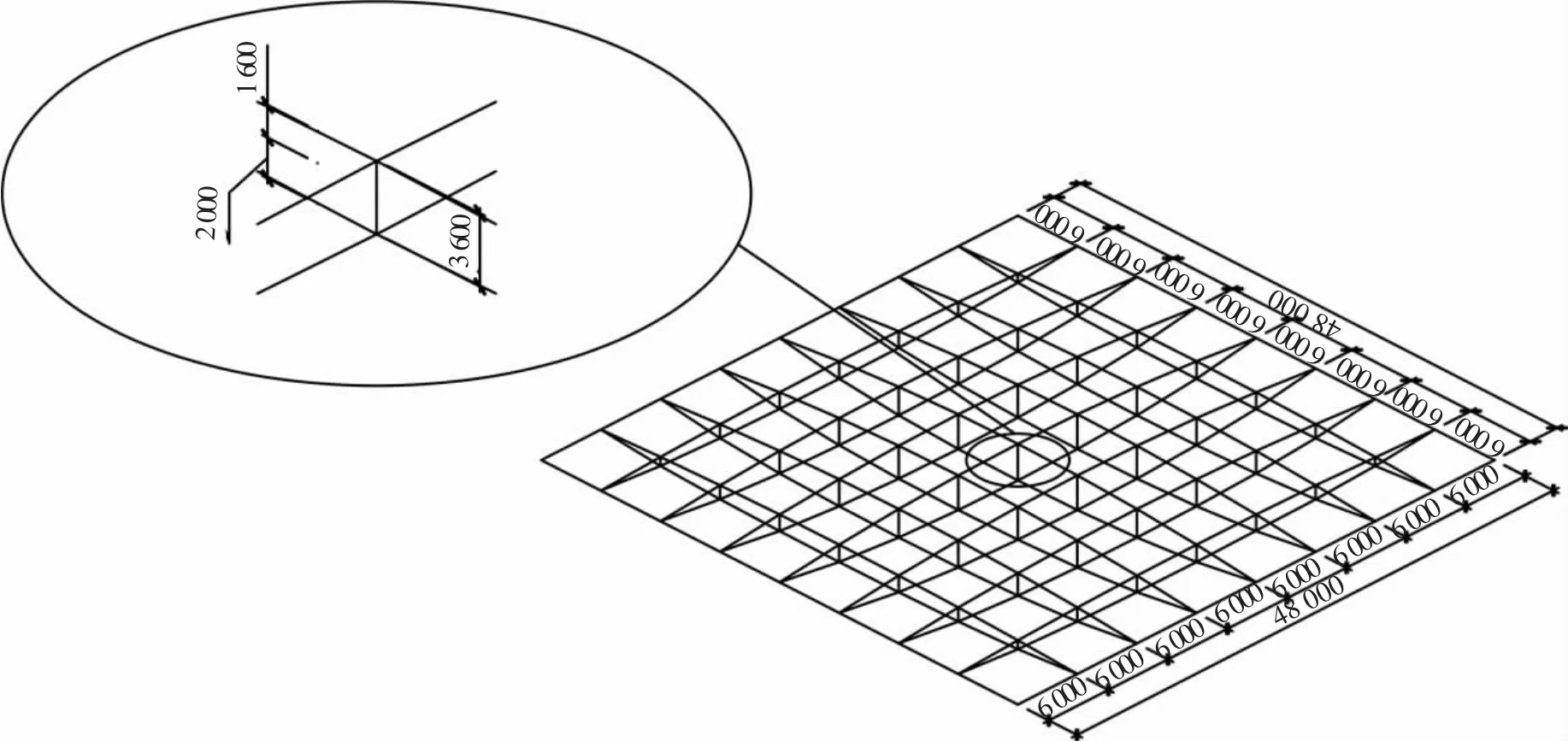
图1 某购物中心双向张弦梁结构布置图(mm)

2 参数分析

设单榀张弦梁的梁高为fu，索网垂度为fb，x(y)方向各榀张弦梁的间距为Sa(Sb)，x(y)方向跨度为La(Lb)，单榀张弦梁如图2所示.

图2 单榀张弦梁的几何参数

2.1 高跨比对优化结果的影响

保持结构长宽、间距、索网垂度以及所取平衡荷载值等参数均不变，分别选取高跨比fu/L=0、1/120、1/60(2/120)、1/40(3/120)、1/30(4/120)、1/24(5/120)、1/20(6/120)、7/120、1/15(8/120)，分析其对双向张弦梁以结构用钢量最小为目标的优化结果的影响.

图3给出了双向张弦梁高跨比对结构的优化影响结果.从图3(a)可知，双向张弦梁高跨比对结构上弦梁用钢量的影响显著，随着高跨比的增加，结构的刚度逐渐增大，用钢量近似呈线性递减.在高跨比从0增至1/15，即拱高从0 m增至增加到3.2 m的过程中上弦钢梁用钢量下降了近130 t，即拱高每增加1 m，用钢量可节省16.3 kg/m2.同时，由总钢材用钢量的变化曲线可知，边梁、撑杆和柔性支撑等次要构件不会改变结构整体用钢量随高跨比的变化趋势.从下弦索的用钢量看，高跨比的增大可以逐渐减小索材用量，但变化极其微小.结合图3(b)可知，当双向张弦梁高跨比小于1/20时，结构的用钢量主要由跨中挠度控制，而结构上弦钢梁的应力水平始终较低，保持在60 MPa以下，其间挠度曲线的波动主要是受次要构件截面尺寸的影响所致，但挠度值始终接近挠度限值.当高跨比大于1/20后，在用钢量继续减小的同时，结构竖向刚度的优势更为明显，表现为最小用钢量转变为由上弦钢梁整体和局部稳定控制，此时构件应力显著增大.由图3(c)可知，虽然结构高跨比的增大使得上弦钢梁的构件长度会逐渐增大，但随着截面尺寸的不断减小，上弦用钢量始终保持近似线性递减的态势.可见，双向张弦梁的高跨比对结构的刚度贡献较大，增大高跨比可有效减小用钢量.

2.2 垂跨比对优化结果的影响

取基准模型，保持其他参数不变，仅改变双向张弦梁的下弦索网垂度，分别选取垂跨比fb/L=0，1/120，1/60(2/120)，1/40(3/120)，1/30(4/120)，1/24(5/120)，1/20(6/120)，7/120，1/15(8/120).同时建立无索的交叉梁系空间钢结构和无索的框架梁系空间钢结构模型，以分析对比下弦预应力索对优化结构的影响.

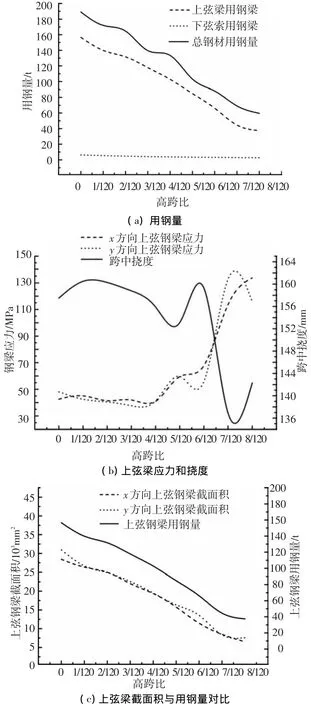
图3 高跨比对优化结果的影响

垂跨比对优化结果的影响在图4中进行了对比分析.结合图4(a)和4(c)可知，与高跨比影响相似，垂跨比的增加可以有效地增大结构的刚度.垂跨比从0增至8/120，即垂度从0 m增至3.2 m的过程中，上弦钢梁用钢量下降了近120 t，但对比选取仅增加同样大小的高跨比或垂跨比，前者可以同比更节省钢材.同时，从上弦梁用钢量随垂跨比增加的曲线走势看出，曲线呈阶梯状，即垂跨比在1/40～1/30和1/24～7/120两个区间内上弦梁用钢量的变化很小.此外，与传统观念不同，虽然增加垂跨比会增大单根索的长度，但由于索应力的下降，下弦索用钢量随垂跨比的增加线性递减，但就整个结构总用钢量而言，其影响不大.同样，次梁、撑杆和柔性支撑等次要构件也基本不会影响结构用钢量随垂跨比变化的总体走势.由图4(b)可以看出，在用钢量优化过程中，跨中挠度始终是控制指标，随着后期垂跨比的增加，钢梁应力也会有所增加.

图4(d)中横坐标上点GriB表示交叉梁系空间钢结构，其荷载传递方式和受力特点类似单层网壳，模型的建立方式与双向张弦梁完全一致，仅去除了下弦索网单元;点Frame表示框架梁系空间钢结构，其荷载传递路径主要为单向，次梁主要起纵向支撑作用，模型建立的方式除将次梁各杆件与主梁的连接变为铰接且去除下弦索网单元外，其他均与双向张弦梁基准模型保持一致.从图中曲线走势不难看出，下弦预应力索网的存在对节省结构钢材的作用是十分明显的.相对于下弦索垂度为零时，不布置下弦预应力索网的交叉梁系空间钢结构用钢量将增大145.2%，框架梁系空间钢结构的用钢量则增大了91.1%.可见，相对于传统空间钢结构，空间预应力钢结构的优势是毋庸置疑的.

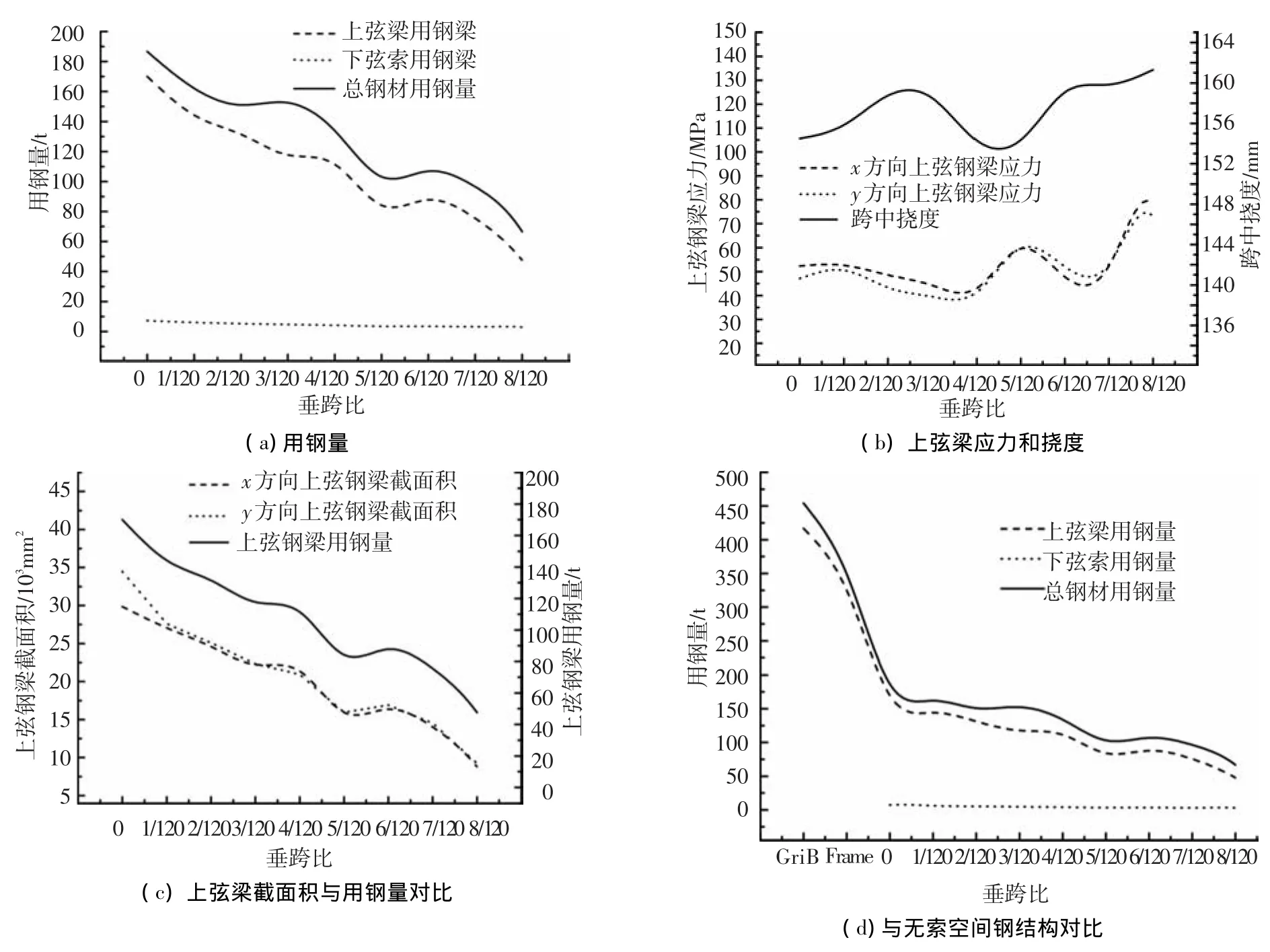
图4 垂跨比对优化结果的影响

由于垂跨比的增加需牺牲建筑内部空间的净高，加之结构用钢量随垂跨比的增加，下降速率不均匀，效果不如增加上弦钢梁的拱高，因此增加拱高的优势显于增加下弦索垂度.

2.3 两向间距比对优化结果的影响

选取基准模型，保持其他参数不变，仅改变x方向各榀张弦梁间的间距，取x方向各榀间距与y方向各榀间距之比分别为Sa/Sb=2/3、4/5、1、4/3、2，分析其对优化结果的影响，如图5所示.此外，本节还与单向张弦梁进行了对比，单向张弦梁用Sa/Sb=8表示，模型为交叉梁系在y方向布置间距为6 m的7榀横向张弦梁，x方向仅布置间距为12 m的3榀纵向梁的单向张弦梁结构.

结合图5(a)、5(c)知，随着x方向间距的增大，y方向张弦梁的榀数不断减少，刚度减弱，因此y方向各榀张弦梁的截面积随着两向间距比的增加而增大，但从上弦钢梁用钢量曲线图看出，整条曲线基本保持水平，差值在4%以内.与此类似，下弦索用钢量随两向间距比的变化也不大.总钢材用钢量随两向间距比的增大呈现先减小后增大的趋势，在两向间跨比等于4/3时达到最小值，相对最大值减小了10%.从图5(b)看出用钢量的优化始终以跨中挠度为控制指标，两向钢梁的应力分布较为均匀.由图5(d)、5(e)可知，当采用单向布索时结构用钢量会有所增加，同时两个方向上弦钢梁的最大应力差值会较双向张弦梁结构明显增大.

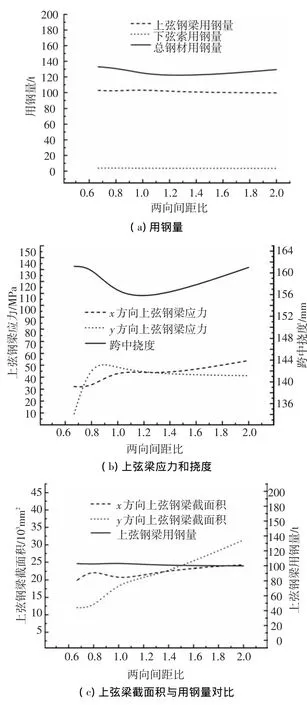
图5 两向间距比对优化结果的影响

可见，对于中小跨度的双向张弦梁，改变两个方向各榀张弦梁的间距对结构的上弦钢梁的用钢量影响不大，但间距比过小或过大会增加支撑体系构件等次要构件的用钢量.总体而言，双向张弦梁结构体系开间的布置还是具备较大的自由性和灵活性的.

2.4 结构长宽比对优化结果的影响

选取基准模型，保持其他参数不变，仅改变x方向的总跨度，选取长宽比分别为La/Lb=0.5、0.75、1、1.25、1.5、1.75、2，分析其对优化结果的影响，同时还与相对应的单向张弦梁进行对比，如图6所示.由图6(a)～6(c)可知，双向张弦梁结构最小用钢量随长宽比变化的优化过程始终以跨中挠度为控制变量，两个方向上弦钢梁的应力水平始终维持在50 MPa左右.随着长宽比的增加，结构的竖向刚度逐渐减弱，需要以加大上弦钢梁截面积来进行平衡.在长宽比不大于1时，上弦钢梁截面积的增大速率较快，之后增大幅度渐趋平缓，但由于结构平面的增大，用钢量的增涨幅度在长宽比大于1.25后与长跨比从0.5到1其间基本一致.长宽比在1～1.25之间时结构钢材用钢量出现一个水平过渡区.也就是说，对于中小跨度的双向张弦梁，长宽为48～60 m是一个较为经济的跨度.此外，下弦索材用量随长宽比的增大也逐渐增加，但相对钢材增幅基本可以不予考虑.

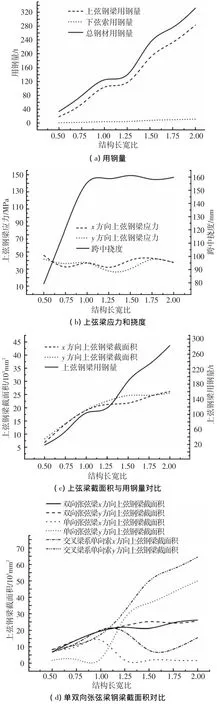
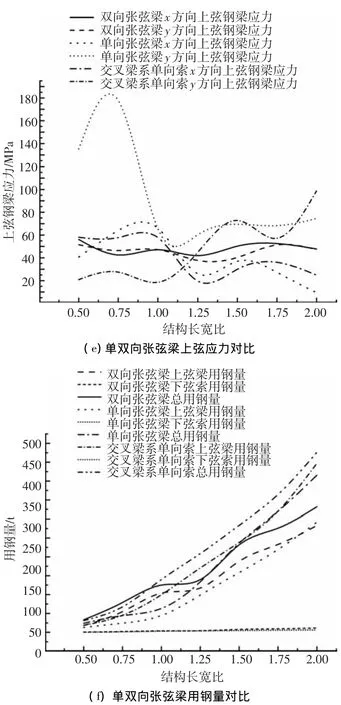
图6 结构长宽比对优化结果的影响

为了直观地比较单向张弦梁与双向张弦梁，本节还考察了与基准模型各参数相同的交叉梁系单向张弦梁结构以及框架梁系单向张弦梁随长宽比变化的结构用钢量优化结果.交叉梁系单向张弦梁结构是指上弦钢梁为交叉梁系，受力类似于单层网壳，索沿其中一个方向的梁轴线布置.框架梁系单向张弦梁是指上弦一个方向为连续梁，另一方向的次梁仅起纵向支撑的作用，也是现在工程中常用的单向张弦梁结构类型.由图6(d)可以清晰观察到，随着结构长宽比的增大，结构的跨度不断增加，使得结构的竖向刚度逐渐减弱，因此需要加大上弦钢梁的截面尺寸予以平衡.优化结果显示，结构长宽比小于1时交叉梁系单向张弦梁和框架梁系单向张弦梁的上弦钢梁截面积都略小于双向张弦梁;当结构长宽比大于1后，x方向梁(即不布置索的梁)截面积出现先减小后逐渐稳定或有所增大的现象，因为单向张弦梁是以单向传力为主的结构，随着x方向梁跨度的增大，这种传力特点更为明显，但当此方向梁跨度增大较多，即大于72 m后，由于竖向刚度减弱加大，为了保证正常使用状态下的跨中位移限值，梁的截面积不能再减小甚至需要加大来提高梁跨间的刚度.更需要的重视的是，此时沿长跨方向布置的各榀张弦梁上弦钢梁(y方向上弦钢梁)截面积均表现为持续的急剧增大.由图6(f)可知交叉梁系单向张弦梁结构和框架梁系单向张弦梁结构的用钢量随结构长宽比的增大呈现不断增大的趋势且速率逐渐加大.前者在长宽比小于1时用钢量略小于双向张弦梁结构用钢量，当结构长宽比大于1后用钢梁明显大于双向张弦梁结构，在长宽比等于2，即结构跨度为48 m×96 m时，交叉梁系单向张弦梁用钢量相对双向张弦梁增大了58%.后者就上弦钢梁用钢量而言，在长宽比达到1.75，即结构跨度为48 m×84 m后超过双向张弦梁，但由于传统的单向张弦梁结构单向传力的特点尤为突出，需要有足够的支撑系统，包括纵向支撑和周边边梁形成完整的空间工作整体，因此，从总钢材用钢量曲线上看到，在长宽比大于1.25后就赶上并逐渐超过双向张弦梁结构，在长宽比等于2，即结构跨度为48 m×96 m时，框架梁系单向张弦梁总钢材用钢量相对双向张弦梁增大了25%.虽然单向张弦梁结构的下弦索用料始终低于双向张弦梁结构，但相对钢材耗钢量而言可以忽略不计.此外，从钢梁应力分布来看，双向张弦梁结构比交叉梁系或框架梁系单向张弦梁结构均匀得多，更有利于抵抗结构在非均布荷载等特殊工况下带来的不利影响.

综上所述，一般业界认为正方形平面布置适宜采用双向张弦梁结构而长方形平面布置采用单向张弦梁结构体系更优的观点在本文的研究结果看来有失偏颇.对于小跨度，即结构跨度小于48 m的结构，采用单向张弦梁结构体系略省钢材，但当跨度大于48 m后，无论是等边的正方形平面布置还是不等边的长方形或椭圆形平面布置均以采用双向张弦梁结构体系更具优势.

2.5 平衡荷载值对优化结果的影响

选取基准模型，仅改变平衡荷载值的选取大小，即分析平衡荷载值(节点力)F=18，27，36，45，54，63，72 kN时对优化结果的影响，如图7所示.

由图7(a)～7(c)可以看到，随着所取平衡荷载值的变化，结构最小用钢量的优化过程始终以跨中挠度控制，两个方向上弦钢梁的应力水平相近且较低.随着所取平衡荷载值的增大，索的用材量变化不大，但最小用钢量优化曲线和上弦钢梁的截面尺寸优化曲线都会出现一个极值点.这是因为平衡荷载值决定着预应力度的取值，预应力的大小对结构在荷载态的刚度有着直接的影响.预应力取值过小，在最大竖向荷载作用下结构应力过大，需要加大截面尺寸以增大结构强度和刚度;预应力取值过大，在风吸力或预应力施工阶段可能引起反向挠度过大或结构强度不够，也需加大构件的截面尺寸.因此.只有当预应力取值合适，即平衡荷载值取值合适时才能得到最优结构方案.图中显示45 kN对于基准模型而言是个相对合适的平衡荷载取值.

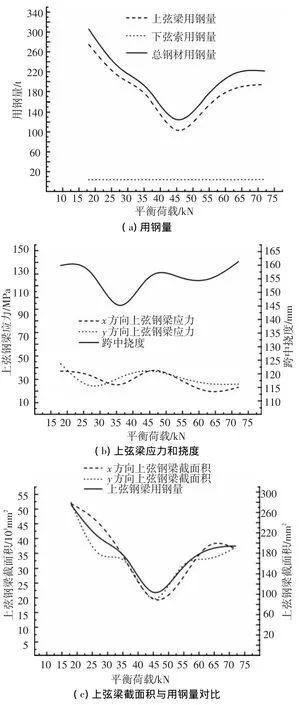
图7 平衡荷载值对优化结果的影响

如第1节中所述，由本算例的计算结果，基准模型在平衡荷载为每个节点45 kN(1.25 kN/m2)时优化后的结构自重为0.548 kN/m2，小于最小竖向荷载0.75 kN/m2，因此对于该优化后的结构平衡荷载值应取为(0.548+1.75)/2=1.149 kN/m2，即每个节点41.364 kN，该值与分析工况F=45 kN最为接近，因此图中显示45 kN时为极值点.

在以往对张弦梁结构的分析研究中对预应力的作用观点不一.文献［3-4］认为张弦梁结构随着预应力的增大，结构内力应该增大.文献［11-12］认为在预应力较小的情况下结构的内力是减小的，因此可减小截面尺寸.文献［13］认为随着预应力值的改变，结构用钢量变化不大，预应力的主要作用在于调节结构在使用荷载作用下的变形.事实上，通过本文的分析发现，预应力的大小取决于平衡荷载值的大小，而平衡荷载值是存在最优值的，此最优值通过已知的结构自重、竖向最小荷载值和竖向最大荷载值即可确定.

3 结论

1)通过分析研究，建议48 m跨度以上的矩形平面结构均可优先考虑采用双向张弦梁结构，受力更为合理.

2)在设计双向张弦梁结构时，尽量增大高跨比是最合理经济的方法;在不影响室内净高的条件下加大垂跨比也是提高结构刚度、减小用钢量的有效措施;可以根据建筑内部的开间大小和平面布置的需要来确定双向张弦梁的两向间距比.

3)双向张弦梁结构预应力索中的预应力取值由平衡荷载的大小决定，而平衡荷载存在最优值，由结构自重、竖向最小荷载和竖向最大荷载三者确定.

［1］SAITOH M，OKADA A.The role of string in hybrid string structure［J］.Engineering Structures，1999，21(8):756-769.

［2］SAITOH M.A study on structural characteristic of beam string structure:prestressing for dead load［C］//Summaries of Technical Papers of Annual Meeting Architectural Institute of Japan.Tokyo:AIJ，1987:632-641.

［3］吴祖咸.张弦梁结构的找形和受力性能分析［D］.杭州:浙江大学，2007.

［4］余凯.新型张拉空间结构受力性能研究与优化［D］.西安:西安理工大学，2007.

［5］尚仁杰，刘景亮，吴转琴，等.泊松方程与双向张弦梁找形［J］.力学与实践，2007，29(5):17-20.

［6］吴捷，吕志涛，舒赣平，等.双向张弦梁索网形状优化后的零状态找形研究［J］.建筑结构，2013，43(增1):356-361.

［7］CHU D N.Evolutionary structural optimization method for system with stiffness and displacement constraints［D］.Melbourne:Victoria University of Technology，1997.

［8］GIL L，ANREN A.Shape and cross-section optimization design of a truss structure［J］.Comput＆Structure，2001，79:681-689.

［9］WANG D，ZHANG W H，JIANG J S.Truss shape optimization with multiple displacement constraints［J］.Comput Methods Appl Mech Engrg，2002，191:3597-3612.

［10］吴捷.双向张弦梁结构的形状优化及静动力特性研究［D］.南京:东南大学，2012.

［11］马美玲.张弦梁结构找形和受力性能研究［D］.杭州:浙江大学，2004.

［12］丁博涵.张弦梁结构的静力、抗震和抗风性能研究［D］.杭州:浙江大学，2005.

［13］陈汉翔，舒宣武.预应力值对张弦梁结构受力性能的影响分析［J］.华南理工大学学报:自然科学版，2003，31(5):174-181.