基于切换多胞系统的高超声速飞行器鲁棒控制

吴振东，王 青，董朝阳，李 玮

(1.北京航空航天大学自动化科学与电气工程学院，100191北京;2.北京航空航天大学航空科学与工程学院，100191北京)

由于高超声速飞行器的飞行包线跨度大，在工作包线内呈现出复杂的时变非线性特点，给其控制系统设计带来很大的挑战.针对飞行器的大包线控制问题，工程上常采用增益调度方法设计控制器［1］，设计过程简单，简化了控制器的设计与实现，在高超声速飞行器X-43A的试飞过程中采用了此方法［2］.但是该设计方法控制器参数按开环方式改变，闭环控制系统的稳定性难以从理论上获得保证.

为了弥补增益调度设计方法的不足，近年来学者将切换系统理论应用于高超声速飞行器大包线飞行的控制器设计中［3-5］.文献［3］设计了大包线自适应切换控制器，分析了闭环系统的稳定性，解决了高超声速飞行器巡航段大包线飞行控制问题;文献［4］给出了基于间隙度量的大包线切换LPV控制方法，设计了各子区域的LPV控制器，分析了闭环系统的稳定性.以上文献均保证了大包线飞行控制系统的稳定性，且优化了控制器切换的过渡过程，一定程度实现平滑切换，却难以从根本上消除控制切换带来的输出跳跃.Hou以切换多胞系统描述大包线飞行动态，给出了确保飞行包线范围渐近稳定的控制器插值方法，从根本上克服了传统切换控制的跳跃问题［5］.此外，现有的切换多胞系统大多依赖于公共Lyapunov函数方法实现对控制系统的分析与综合［4-5］，要求多胞的每个顶点和整个多胞区域内都存在一个公共的Lyapunov矩阵函数，具有较大的保守性.本文针对上述问题，将高超声速飞行器包线范围内的飞行动态建模为切换多胞系统，采用基于参数依赖Lyapunov函数与平均驻留时间方法给出包线范围渐近稳定的条件，设计了确保多胞系统在参数任意快变下稳定的反馈控制器，所得控制器能够在保证系统稳定的前提下，克服切换控制器的输出跳跃现象，并降低了系统分析与设计的保守性.

1 高超声速飞行器切换多胞系统建模

以高超声速飞行器［6］的纵向飞行动态为例，不失一般性，仅考虑飞行器的纵向短周期运动，假定每一个工作点处的纵向短周期线性模型可以表征工作点附近的飞行动态.设飞行包线内N个工作点所对应的动力学系统描述为

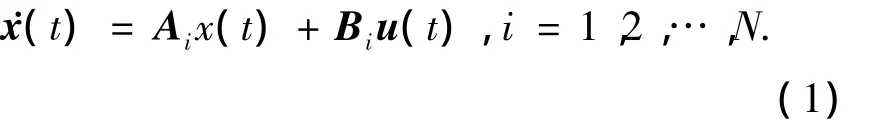
其中:x(t)=［αq］T为系统状态，α，q分别为迎角和俯仰角速率，u(t)=[ξeη]T为控制输入，ξe为升降舵偏转角，η为节流阀调定指令，Ai、Bi分别为飞行包线内第i个工作点的系统矩阵和控制输入矩阵，i为工作点标号.

采用切换多胞系统建立高超声速飞行器包线内的飞行动力学模型过程是将整个包线内的工作点根据调度变量(如马赫数和高度等)划分为不同的组，每组对应包线内的一个区域，以每一区域建模为一个多胞系统，系统的顶点即为该区域内的工作点，顶点的动态特性由工作点处的线性小扰动方程表征，多胞系统内部的飞行动态通过顶点系统动态的线性加权获得，则该区域内的飞行动力学特性由该多胞系统近似描述;然后将各飞行区域视为一个独立的多胞子系统，将飞行轨迹在相邻多胞子系统间的穿越视为子系统间的切换，则整个飞行包线内的飞行动力学可用一个切换多胞系统描述.其中，每个多胞子系统的工作点选取原则是使多胞系统的工作点状态空间模型相差尽量小，这样有利于性能品质的提高，因为若将多个模型相差较大的工作点划分在同一区域，设计控制系统会因为鲁棒性的要求而牺牲指标性能，常用的工作点选取方法可采用奇异值判定方法和间隙度量方法［4］.

需要注意的是，为保证得到的多胞子系统可完整地覆盖整个飞行包线，相邻的多胞子系统需要满足局部重叠的特性［7］，即相邻的多胞子系统需包含公共的工作点.

基于切换多胞系统建立飞行器包线内的飞行动力学模型过程可以图1为例简单说明.考虑高超声速飞行器的再入高度变化从25 km到40 km，马赫数变化从16到14，此包线飞行动态可以由18个工作点处的模型包络，根据马赫数的变化划分成3组，得到3个飞行区域，建立相应3个多胞子系统;工作点5～8为多胞子系统1和2包含的公共工作点，工作点12～14为多胞子系统2和3包含的公共工作点，保证此3个多胞子系统可覆盖整个飞行包线，且当飞行轨迹穿越相邻多胞子系统间的边界时，将其视作飞行动力学多胞系统模型的切换，则整个飞行包线的飞行动力学可采用切换多胞系统描述.

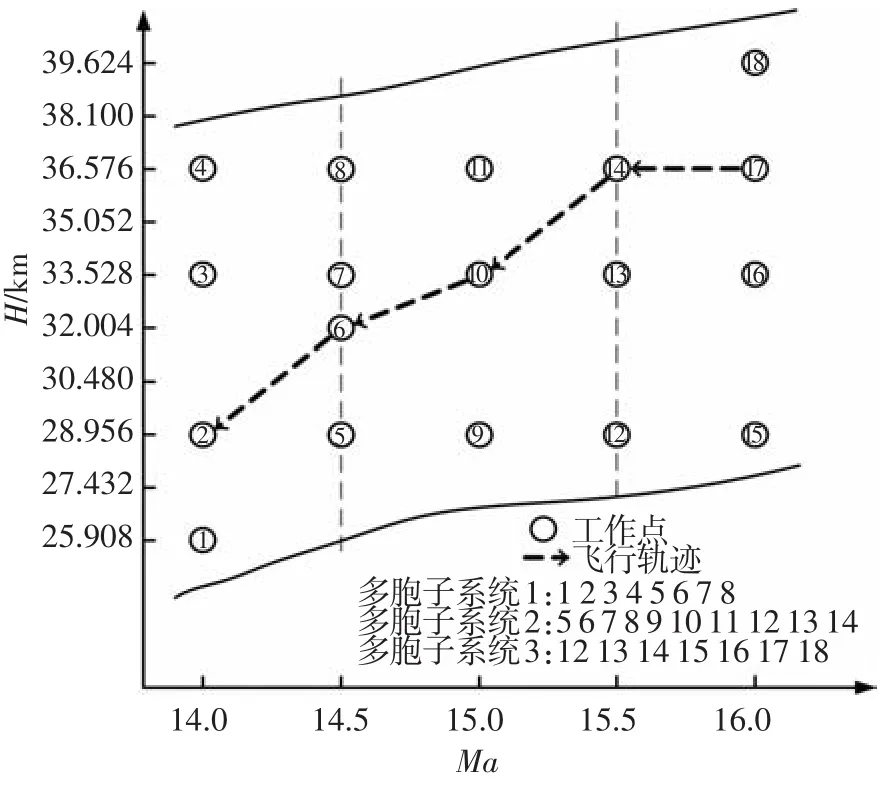
图1 高超声速飞行器的切换多胞系统建模示意图

根据上述的切换多胞系统建模方法，将整个工作点模型集划分为k个子集，相应地，工作点标号全集Ω被划分为子集Ω1，Ω2，…，Ωk.飞行包线内的高超声速飞行器的飞行动态采用不确定性切换多胞系统描述为

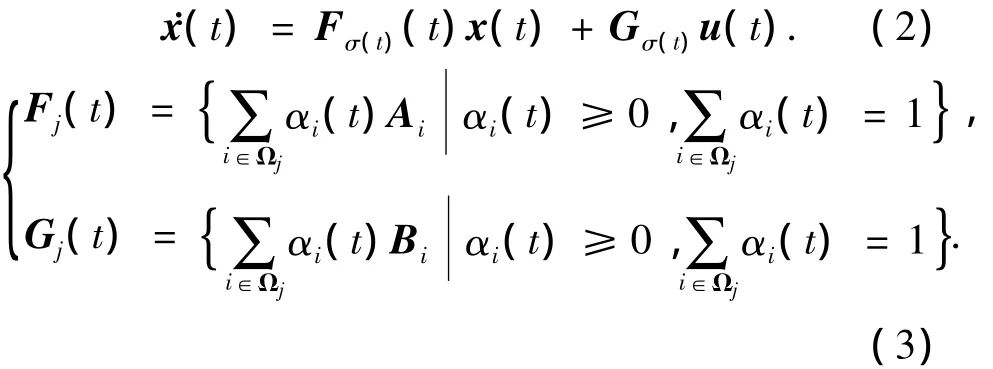
式中:σ(t)∈［0，+∞)→Ω={1，2，…，k}为切换律，表征飞行器工作区域随时间变化规律;j∈S，S={1，2，…，k}为切换律的索引集;k为飞行包线内多胞子系统的个数;j为工作点所在工作区域的标号，子系统Ωj要满足多胞系统模型对飞行器所有工作点完全覆盖的条件Ωj=Ω，且要保证相邻的多胞子系统间的公共子系统满足=Ωj∩Ωj+1≠Ø.

由于邻近的两个多胞子系统公共边界上的飞行动力学仅由多胞子系统公共设计点的飞行动力学得到，因此，切换多胞系统的切换不会引起系统矩阵参数不连续的变化，即对于整个飞行包线来说，Fσ(t)和Gσ(t)是连续变化的.

飞行器控制系统设计任务是实现控制系统的稳定和对给定指令信号的跟踪控制，针对高超声速飞行器的切换多胞系统(2)，设计控制器为

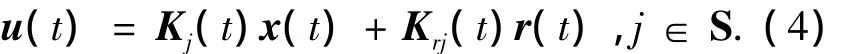
式中:Kj(t)、Kri(t)分别为控制器中的反馈控制律和前馈控制律，r(t)为给定的指令信号.

2 控制器设计和稳定性分析

定义1 对切换多胞系统(2)的切换信号σ(t)，令 ΔT＞0为公共子系统工作总时间，Nσ(ΔT)为ΔT内的切换次数.若存在N0≥0，τa＞0，使得成立，则称 τa为平均驻留时间，下文中以 T［τa，N0］表示满足平均驻留时间的切换律集合.

针对切换多胞系统(2)中的单个多胞子系统，给出如下稳定性引理.

引理1［8］多胞线性系统(2)的自治多胞子系统鲁棒稳定的充分条件为存在正定矩阵Pi(i∈Ωj)及适维矩阵Yi满足矩阵不等式

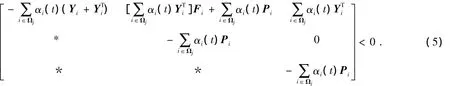
引理1通过引入松弛变量Yi，使得矩阵不等式中不再出现正定矩阵与系统矩阵的乘积项，降低了反馈控制综合问题的求解难度［9］.式(5)矩阵不等式中的*表示矩阵中元素所在位置对称块的转置，下文中与此表示的意义一致.

定理1 对于切换多胞系统(2)，若多胞子系统的顶点，存在矩阵Pi(i∈Ωj)，适维矩阵Ui及Vi满足

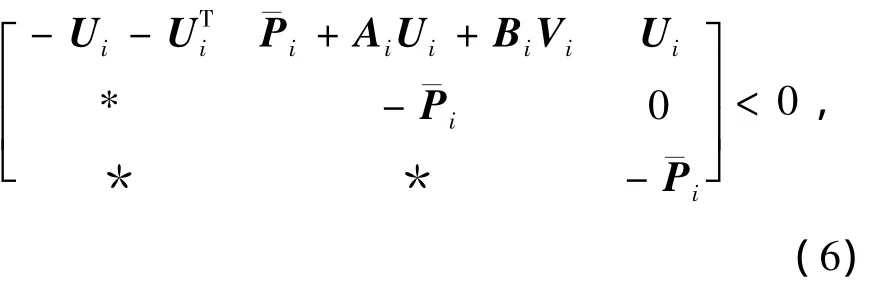
且切换多胞系统切换律σ(t)∈T［τa，N0］满足平均驻留时间τa约束

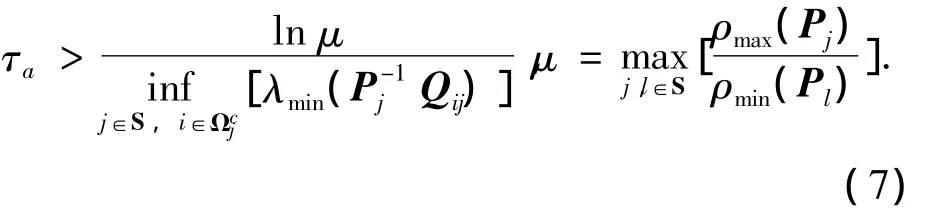
式中:ρmax(·)，ρmin(·)分别为矩阵的最大奇异值和最小奇异值，λmin(·)为最小特征根，Qij由公共子系统工作点求取.则控制器(4)中镇定反馈控制器Kj(t)的参数选取为

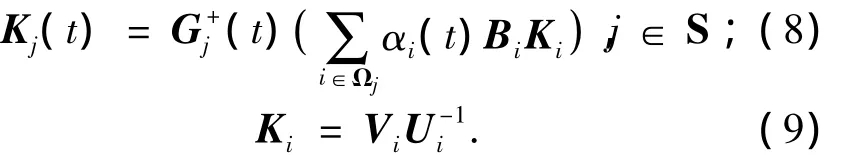
可保证对任意切换律σ'(t)∈T［τa，N0］，闭环切换多胞系统在零输入情况下渐近稳定.其中，(t)是(t)的M-P伪逆.

证明 设存在正定矩阵(i∈Ωj)，适维矩阵Ui及Vi满足线性矩阵不等式组(6)，下面首先证明式(9)给出的控制器增益矩阵使得切换多胞系统鲁棒稳定.

由式Ui+UTi＞0，可知Ui可逆，则式(9)中矩阵Ki的存在性显然.用diag{Ui-1，Ui-1，Ui-1}对式(6)进行全等变换可得

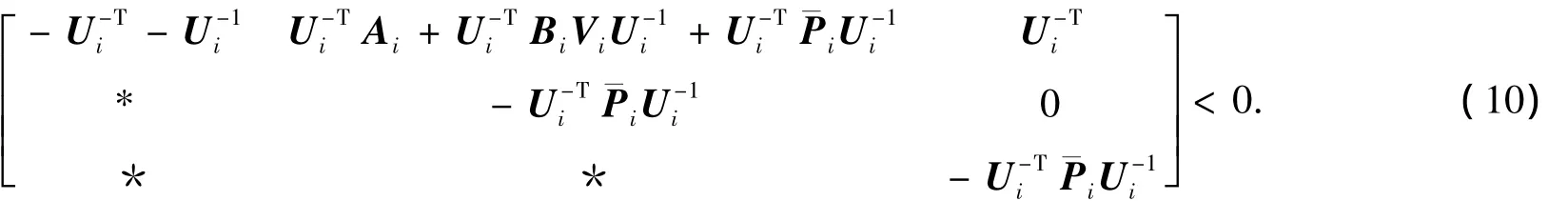
假设第p和q个多胞子系统间的公共子系统工作时长为t*，则有

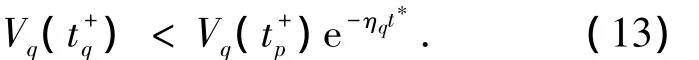
其中:

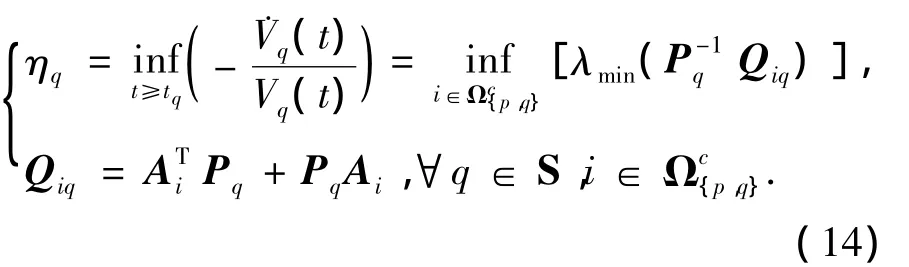
将式(14)代入式(13)，有

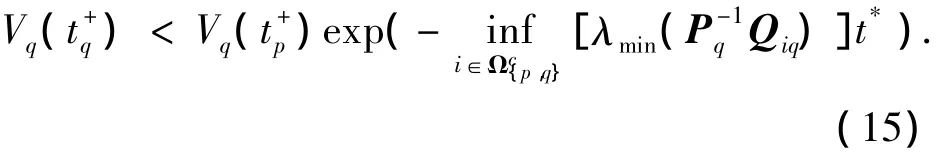
结合式(15)和式(16)，可得

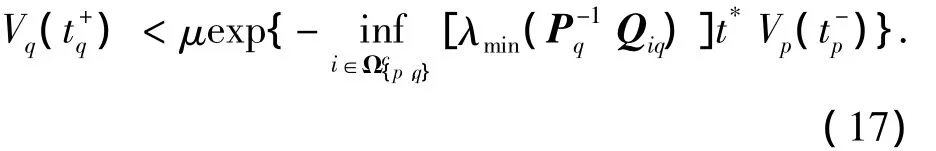
以t1，t2，…，tNσ(ΔT)分别表示各公共子系统相继激活时刻，且各子系统工作时间分别为Δt1，Δt2，…，ΔtNσ(ΔT)，显然，ΔT=Δt1+Δt2+…+ΔtNσ(ΔT).将多胞公共子系统从1到Nσ(ΔT)重复，如式(13)的推导方式，并结合式(17)，有

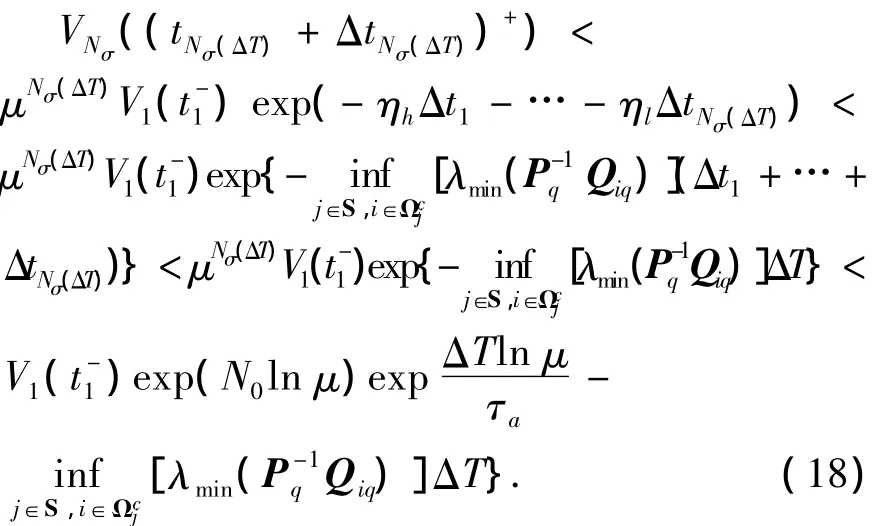
由式(7)可知

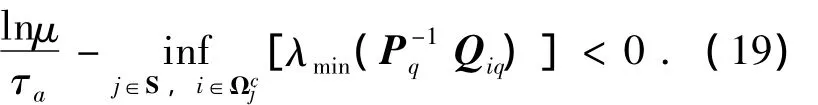
也即当ΔT→+∞时，必然存在ΔT*＞0使得下式成立.

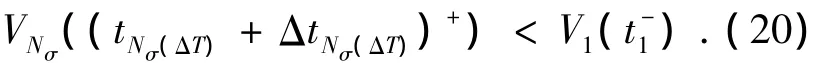
由上式可知多胞子系统之间切换时Lyapunov函数值单调递减，同时，考虑到任意多胞系统在子切换律作用下Lyapunov函数值递减，因此，切换多胞系统(2)在切换律σ(t)∈T［τa，N0］作用下全局渐近稳定.

文献［5］中对P作了较为苛刻的限制，要求多胞子系统的每个顶点(即整个多胞系统)都存在一个共同的Lyapunov函数矩阵P，因而具有较大的保守性，而定理1要求对于切换多胞子系统的顶点i，可以存在不同的正定矩阵Pi满足式(6)，即相对而言，定理1具备更低的保守性.

定理1中式(8)所示控制器Kj(t)的形式可视为对区域内边界工作点的状态反馈增益阵插值，需要实时获得σ(t)和α(t).这在实际飞行中很容易实现，将所有工作点处的高度和马赫数以数据表的形式装订至控制器，传感器实时测量高度和马赫数，控制器通过查表和插值方式获得权值向量σ(t)和α(t)，由于飞行器动态在飞行区域内部及飞行区域间变化的连续性，即α(t)的连续性，保证了控制器插值的连续性，进而确保了控制器输出不会发生跳变.

为了使系统的输出y(t)跟踪有界分段连续的参考指令信号r(t)，控制器(4)中前馈控制律Krj(t)参数选取为

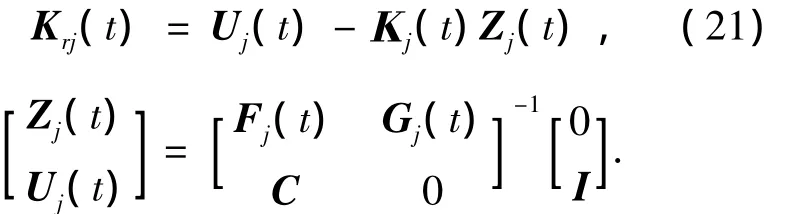
式中:C为系统输出矩阵.在系统镇定的情况下，按式(21)设计的前馈控制律Krj(t)可以实现对给定指令信号r(t)的无差跟踪［10］.

3 仿真验证

为验证本文方法的有效性，采用文献［6］的高超声速飞行器模型，大包线内控制器的综合以包线内18个工作点为基础，如图1所示，所选择的工作点以马赫数和高度为调度变量，各工作点的平衡条件见表1.

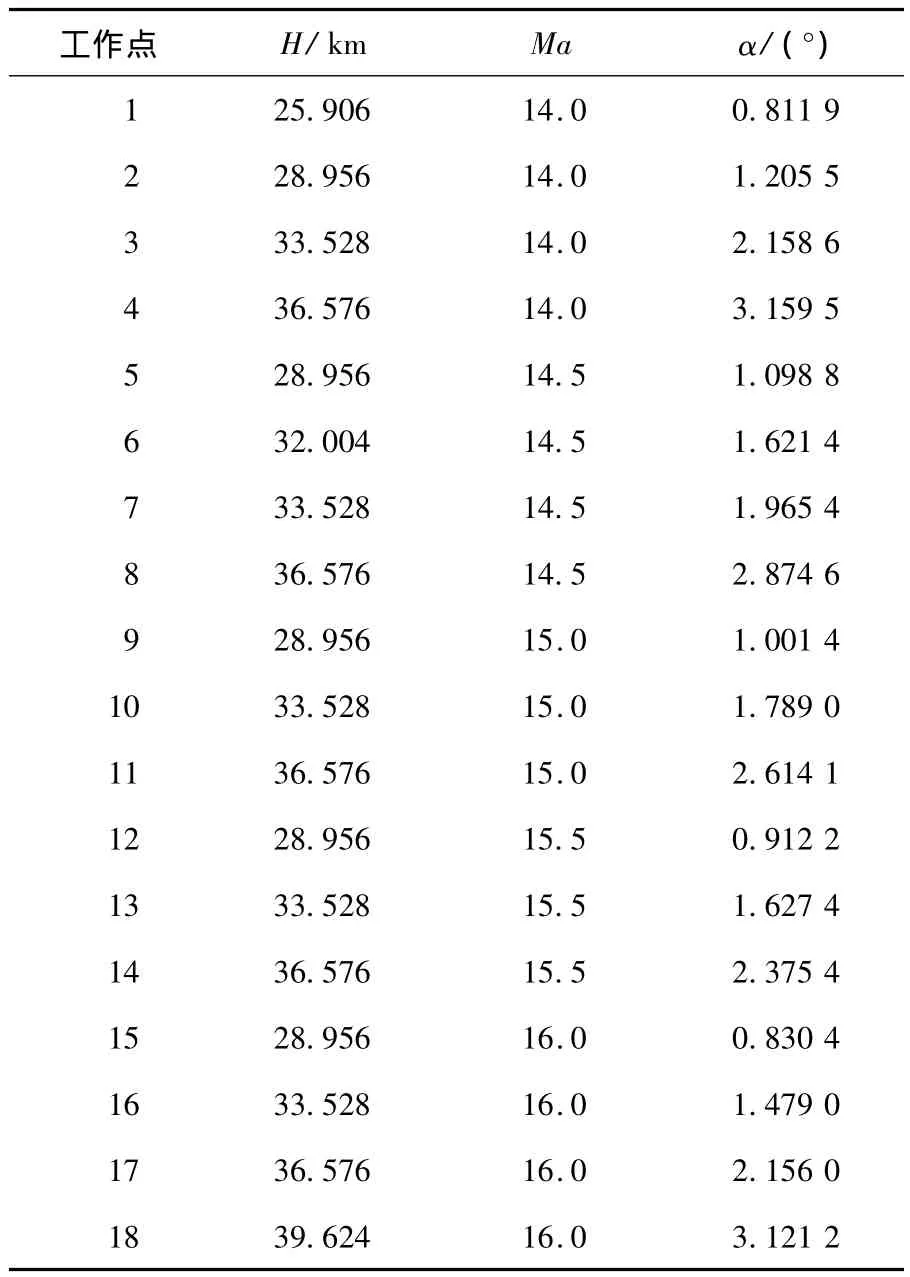
表1 高超声速飞行器飞行包线范围内的工作点

根据前述的切换多胞系统建模方法，飞行包线内所选择的18个工作点可根据马赫数分成3组，即建模为3个多胞子系统，各多胞子系统包含的工作点为

由定理1获得切换多胞系统的各工作点控制器增益Ki如表2所示，对于每一个多胞子系统，子状态反馈控制器Kj(t)采用式(8)进行插值，前馈控制律Krj(t)依据式(21)进行计算，给定C为单位阵.以包线内Ma∈［14.5，15)，H∈［29，36.5)的飞行区域说明状态反馈控制器Kj(t)的插值过程:在此飞行区域内，子控制器的镇定反馈控制增益通过设计点5、8、9和11上的4个反馈控制增益K5，K8，K9，K11进行插值得到，对于该飞行域内的某一特定的高度hx和马赫数Max，插值得到的镇定反馈控制增益K为

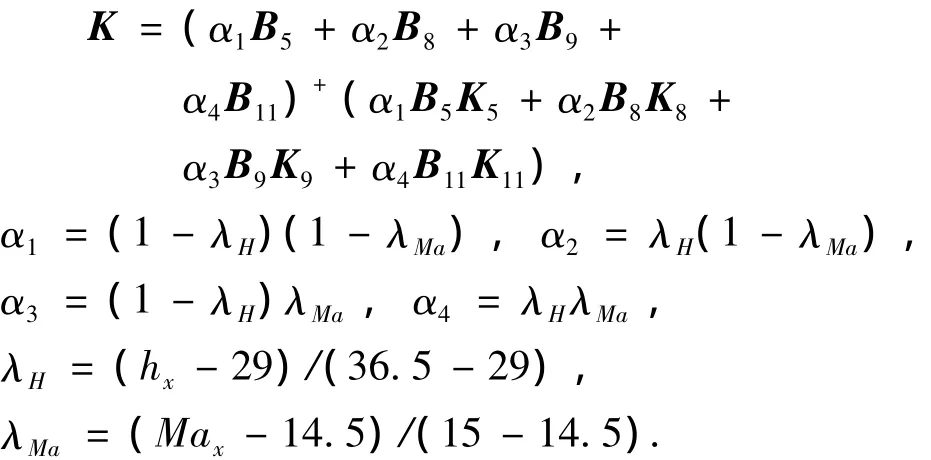
表2 工作点处的控制器增益

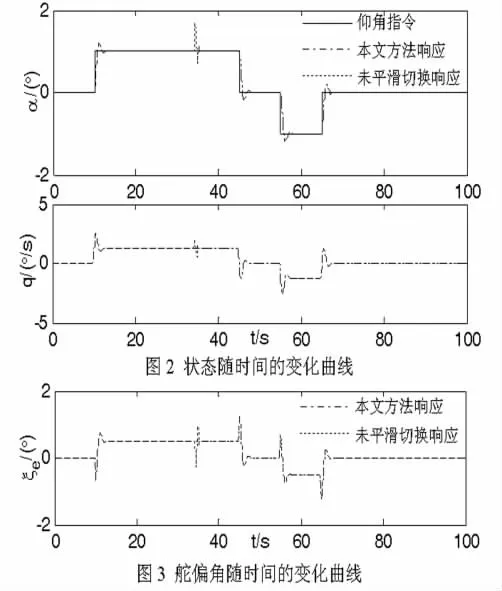
不失一般性，考虑高超声速飞行器的工作点变化轨迹17—14—10—6—2，可见在工作点14、6处发生多胞切换，仿真结果如图2、3所示.

由仿真结果可知，本文方法可以很好跟踪参考信号，升降舵偏角处于安全工作范围，体现了控制器良好的性能，与未考虑平滑切换相比，在工作点切换时刻无控制器输出跳跃现象.在控制器设计保守性方面，采用文献［5］的模型，在飞行器工作点区域划分等初始条件相同的情况下，依定理1计算可得切换多胞系统平均驻留时间下限为2.332 7 s，低于文献［5］的6.937 8 s，该结果表明定理1具有较低的设计保守性.

4 结论

1)提出一种基于切换多胞系统的高超声速飞行器鲁棒镇定控制方法.针对飞行器大包线飞行参数时变的镇定与稳定性分析问题，将高超声速飞行器包线范围内的飞行动态建模为切换多胞系统，采用基于参数依赖Lyapunov函数与平均驻留时间方法给出包线范围渐近稳定的条件，设计了确保多胞系统在参数任意快变下稳定的控制器.

2)仿真结果表明，提出的控制器既能够保证系统稳定，又克服了切换控制器的控制量跳跃现象，并降低了系统分析与设计的保守性.

［1］RUGH W J，SHAMMA J S.Research on gain scheduling［J］.Automatica，2000，36(10):1401-1425.

［2］HOLLAND S D，WOODS W C，ENGELUND W C.Hyper-X research vehicle experimental aerodynamics test program overview［J］.Journal of Spacecraftand Rockets，2001，38(6):828-835.

［3］谈树萍，李智斌.高超声速飞行器自适应切换控制及稳定性分析［J］.空间控制技术与应用，2011，37(1):21-27.

［4］张增辉，杨凌宇，申功璋.高超声速飞行器大包线切换LPV控制方法［J］.航空学报，2012，33(9):1706-1716.

［5］HOU Yanze，WANG Qing，DONG Chaoyang.Gain scheduled control:switched polytopic system approach［J］.Journal of Guidance Control and Dynamics，2011，34(2):623-628.

［6］BOLENDER M A，DOMAN D B.Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle［J］.Journal of Spacecraft and Rockets，2007，44(2):374-387.

［7］HOU Yanze，DONG Chaoyang，WANG Qing.Stability analysis for switched linear systems with locally overlapped switching law［J］.Journal of Guidance Control and Dynamics，2010，33(2):396-403.

［8］PEAUCELLE D，ARZELIER D，BACHELIER O，et al．A new robust d-stability condition for real convex polytopic uncertainty［J］.Systems＆Control Letters.2000，40(1):21-30.

［9］DAAFOUZ J，RIEDINGER P，IUNG C.Stability analysis and control synthesis for switched systems:a switched Lyapunov function approach［J］.IEEE Transactions on Automatic Control，2002，47(11):1883-1887.

［10］TAN Feng，DUAN Guangren，ZHAO Lijun.Robust controller design for autopilot of a BTT missile［C］//Proceedings of the 6th World Congress on Intelligent Control and Automation.Dalian:Dalian Univesity of Technology Press，2006:6358-6362.