地铁车站结构随机振动响应分析

马乾瑛，刘志钦，王社良，熊二刚

(1.长安大学建筑工程学院，西安 710061;2.河南城建学院土木与材料工程系，河南平顶山 467036;3.西安建筑科技大学土木工程学院，西安 710055)

地铁车站结构随机振动响应分析

马乾瑛1，刘志钦2，王社良3，熊二刚1

(1.长安大学建筑工程学院，西安 710061;2.河南城建学院土木与材料工程系，河南平顶山 467036;3.西安建筑科技大学土木工程学院，西安 710055)

基于地震反应的随机非确定性，运用基于概率统计方法的随机振动理论进行结构抗震分析，考察结构的动力可靠度，是一种合理的设计方法。运用虚拟激励法对青岛地铁五四广场站进行随机振动分析，避免了传统方法计算的冗繁，得到了具有统计意义的结构动力响应。考虑x向功率谱输入时，弯矩分布较为均匀;地铁结构体型变化较大的部位剪力明显增大;柱底剪力较小，边跨柱剪力小于中跨柱底剪力。考虑y向功率谱函数输入时，沿梁轴向剪力值逐渐增大，柱底剪力明显大于x向输入时的柱底剪力，边跨柱柱底剪力大于中跨柱底剪力。所得结论为地铁站这一复杂结构形式进行基于可靠度理论的设计提供了依据，可以作为同类设计的参考指导。

地铁车站;虚拟激励法;随机振动

1 概述

地下交通是未来解决城市交通拥堵问题的主要途径。目前，全国已有34个城市规划了轨道交通建设项目。据介绍［1］，到2015年，全国地铁运营总里程将达3 000 km;2020年，将有40个城市建设地铁，总里程达7 000 km，是目前总里程的4.3倍。地铁在解决交通问题的同时又具有人防工程的作用，因此，保证地铁结构的安全性与稳定性对人民生命财产的保障以及城市生活的正常运行有着极为重要的意义。通常认为，周围土体对地下结构具有良好的约束作用，因此地下结构具有较好的抗震性能［2］。实际上，已有的震害表明，由于地震荷载具有巨大的破坏力与突发性，在地震作用下，现有的地下结构并不安全，甚至可能会发生严重破坏，其中地铁车站破坏最为严重，由于中柱的坍塌可导致顶板结构破坏和沉降发生。地铁结构一旦遭受破坏，会给地震应急和震后修复带来极大的困难。所以，在设计地下结构时应充分考虑地下结构的抗震安全与稳定性。

2 地铁车站抗震计算

地震作用时，与地面以上结构相比［3］，地下结构由于受到周围土体的约束作用显著，结构的自振特性一般不明显，相应地，结构振动对周围土体的影响较小;结构地震动力响应与结构埋深和地震加速度的关系不明显;而结构与边界土体的共同作用对结构的动力响应有重要影响，承受的荷载多且变化较大，对地震波入射方向敏感以及与周围地基土的相互作用等特点，决定了其抗震设计方法不能采用地面结构的方法。

目前，地下结构的抗震设计方法主要有波动法和相互作用法两种［4］，波动法将地下结构和周围土体作为一个整体进行考虑，忽略结构对波动场的影响，以波动方程为基础，求解得到结构与土体中各自的应力场和波动场;相互作用法通过弹簧和阻尼对结构周围土体进行模拟，以结构为主体，建立结构运动方程，求解得到结构的地震响应和结构与土体之间的相互作用力。

然而，地下结构抗震设计的两种方法基本上都是“定值分析”，即将结构与外部荷载均作为不变的参数进行建模分析［5］。实际上，地震动具有显著的不确定性和不重复性，当采用确定性的分析方法时，所得到的结果由于具有特定性而不能真实地反映结构的动力响应特征。随着抗震理论的发展，近些年发展起来的结构随机振动理论，采用概率与统计方法研究结构系统的动力响应、稳定性及可靠性，从能量角度分析激励的随机性问题［6］。以功率谱函数作为荷载输入，得到具有统计信息的概率特征值，比定值分析方法得到的结果更具有普遍性和准确性。

在进行结构抗震设计时，应将地震作用视作随机场或至少视作随机过程来处理。随着结构设计理论的发展，应用可靠性理论、推行结构概率设计方法以取代传统的安全系数设计法是当今国内外结构设计发展的必然趋势。因此，应用随机振动理论，开展地下结构抗震可靠性研究，建立地下结构动力可靠度分析的理论体系具有非常重要的现实意义，其研究成果具有非常广阔的应用前景。

3 随机振动理论概述

在随机振动分析中［7］，通常假设地震动是一种平稳的各态历经过程，根据对实际地震记录的功率谱密度分析，得到具有频率特性或无频率特性的功率谱密度函数，以功率谱函数作为荷载输入，采用频域求解方法，得到以概率统计方法定量描述结构振动规律的结果。

对于n个自由度的空间结构，其动力学方程为［8］

考虑式(1)中外荷载加速度的统计意义，即将{¨xg(t)}项替换为其功率谱密度函数S¨xg(ω)，用频域法求解方程，则对结构的分析转换为随机振动分析。然而，由于地震动属于随机动力荷载，具有较宽的频带;同时，地下结构形式复杂，自由度较多，采用通常的频域法难于得到高精度解。

大连理工大学林家浩教授近年来提出的虚拟激励法是一种具有高效率的随机振动求解方法［9］。采用虚拟激励法求解时，通过设置虚拟荷载将随机振动的计算转化为稳态简谐响应分析，将非平稳随机振动的计算转化为普通逐步积分计算，实现了用基本的动力学方法来求解一般的平稳随机振动问题。

根据随机振动理论［10］，线性系统在单点平稳随机激励x(t)下，激励的自功率谱和响应的自功率谱满足

其中，H为频率响应函数，同时，简谐荷载eiωt下的简谐响应为

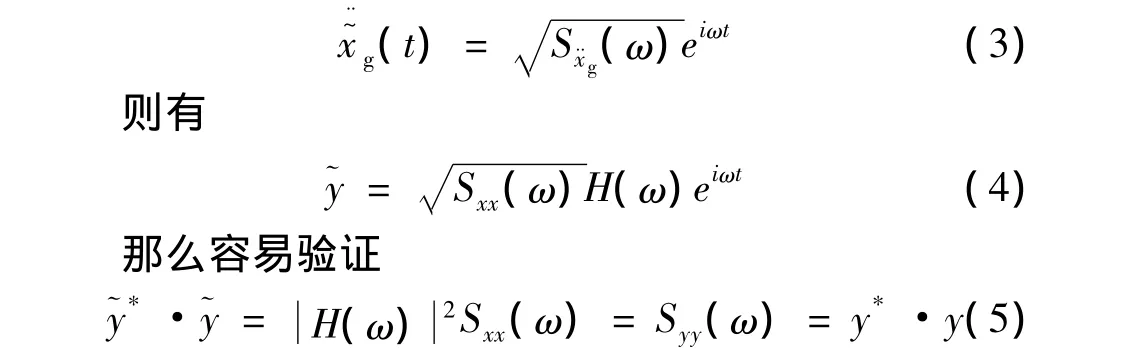
式(2)～式(5)是虚拟激励法的基本原理。虚拟激励法在求解过程中包含了所有参振振型和所有随机激励之间的耦合项［11］，本质上是精确解法，与传统的CQC算法在数学表达上等价，然而与计算q阶振型的CQC法相比，其计算量仅为CQC法的1/q2;即使与忽略了振型耦合项的SRSS法相比，其计算量也仅为SRSS法的1/q。

将欧拉公式带入式(3)中，可以得到

将式(6)代入到式(4)中，根据文献中的方法，分别进行简谐激励下结构的动力时程分析，叠加得到结构的虚拟位移响应

其中，B(ω)为幅值函数;φ为相位角。

根据虚拟激励法，结构的位移响应功率谱为

由此可知，虚拟激励法使用起来比较简便，在计算中具有较高效率，在普通微机上就可精确而迅速地计算非常复杂的问题。所得到的结构响应功率谱同样具有概率分布意义，可以用来进行结构可靠度的验算。

4 工程概况

青岛地铁一期工程(3号线)五四广场站位于香港中路与山东路交汇处香港中路上，车站长约277.6 m。本车站施工方法为盖挖逆作法，拱顶埋深3.50～6.00 m。选取体型较为复杂的①～○16轴间结构进行随机振动分析，平面布置如图1所示，结构整体3层，其中①～⑧轴间为4柱5跨结构，⑨～○16轴为5柱6跨结构，结构模型如图2所示。

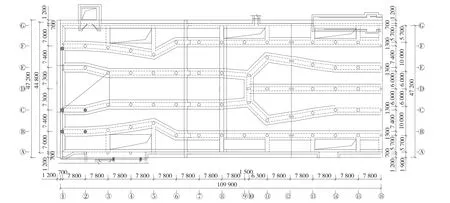
图1 结构柱网平面(单位:mm)

图2 地铁车站结构模型

计算模型总长109.55 m，宽44.1 m。梁、柱及桩采用梁单元模型，墙体及板采用厚板模型，混凝土强度等级为 C45，钢管钢材为Q235，混凝土强度等级为C40。梁、柱、桩截面参数见表1。

表1 截面尺寸 m

顶板恒载为覆土荷载、顶板结构自重，顶板上覆土厚5.9 m，地面超载为20 kN/m2;中板上作用有均布恒载10 kN/m2的设备荷载以及4 kN/m2均布活载;侧板侧向及底板作用有水压力。根据《中国地震动参数区划图》(GB18306—2001)，本场地的地震动峰值加速度为0.05g(抗震设防烈度6度)，地震动反应谱特征周期为0.40 s。

日本学者田村重四郎和冈本舜三在进行沉埋隧道地震反应分析时，假定隧道对周围土体的自振特性没有影响;隧道惯性力对动力性能的影响忽略不计;表面地层的剪切振动基本振型对隧道在地震中产生的应变起主导作用。因此，采取同样的假定，将地铁车站及站体以外土体划分为一系列单元，每一单元均用与其剪切振动自振周期相同的质量-弹簧代替［12］。站体侧面及底面的边界条件简化模拟为仅受压的土弹簧，刚度根据地基系数计算得出;两端与隧道接触处，按刚性连接处理，进行随机振动分析。

选用金井清地震加速度功率谱模型，随机地震动输入功率谱函数为

式中，ωg，ξg分别为覆盖土层的卓越频率和阻尼比。

基于虚拟激励法构造虚拟激励作用于结构，在进行随机振动分析时，频域取 ω∈［0，200］rad/s，频点间隔 Δω =0.1 rad/s。

图3为考虑x向功率谱输入时，地铁车站中层边纵梁沿长度方向剪力及弯矩图，可以看出，①～⑧轴间中纵梁剪力较大，在⑤～⑧轴地铁结构体型变化较大的部位，中纵梁的剪力出现明显增大现象;弯矩沿中纵梁长度方向分布较为均匀，在⑧～○16轴间有增大趋势。与剪力分布情况相同，在支座处，剪力及弯矩均较大。图4为考虑y向功率谱函数输入时，地铁车站中层边纵梁沿长度方向的剪力及弯矩图，可以看出，⑧～○16轴间中纵梁剪力较大，沿梁长方向，剪力值逐渐增大;①～⑧轴间的弯矩较大。同样，在支座处，剪力及弯矩均较大。对比不同方向功率谱函数输入的结构内力响应，进行结构随机振动分析时，功率谱函数的输入方向对结构的动力响应影响显著。

图3 x向输入时中纵梁内力均值

图4 y向输入时中纵梁内力均值

图5为x向、y向输入功率谱函数时柱底剪力比较图，可以看出，x向输入时，柱底剪力较小，边跨柱剪力小于中跨柱底剪力，边跨柱底剪力沿车站长度方向变化不大，中跨柱底剪力在车站两端部位较大，⑨～○16轴间中跨柱底剪力有增大趋势。y向输入时，柱底剪力明显大于x向输入时的柱底剪力，边跨柱柱底剪力大于中跨柱底剪力，①～⑧边跨与中跨柱底剪力差别较大，⑨～跨间C、D、E轴柱底剪力较大且相差不大。

图5 柱底剪力比较

5 结论

随着地铁建设的快速建设与发展，地铁车站结构的抗震设计问题己经成为地铁建设中的一个重要环节，对地铁车站结构进行随机地震反应分析可以求得结构各构件的地震响应功率谱、均值和均方根值，进而确定地铁车站结构地震动力可靠度，为地铁车站结构的可靠性设计提供理论参考依据。通过对青岛地铁五四广场站进行随机振动分析，可以得到:地铁车站结构由于受周围土体约束显著，动力特性不同于地面结构，因此采用随机振动分析能够从概率统计方面得到地体车站结构的地震响应统计值;考虑不同方向的地震功率谱输入时，地铁车站结构动力响应情况显著不同，横向地震对结构的内力影响较大;基于林家浩教授提出的虚拟激励法，对结构进行随机振动分析时，将平稳随机外力转化为简谐外力，可以高效地解决随机振动分析时计算精度和计算效率之间的矛盾;本文对地铁车站结构的分析方法可以为同类的设计提供参考，地铁车站结构设计时应充分考虑场地土的差异、土体液化等边界约束情况以及符合场地条件具有统计规律的地震动功率谱模型的合理选取。

［1］ 人民网.2015年地铁运营线达3 000 km十二五期间投资或超万亿.［EB/OL］.http://finance.people.com.cn/GB/70846/16472936.html.2011.12.02.

［2］ 于翔.地下建筑结构应充分考虑抗震问题—1995年阪神地震破坏的启示［J］.工程抗震，2002(4):17-20.

［3］ 还毅，方秦，柳锦春，陈力，杜茂林.提高地铁车站结构抗震能力的理论及数值分析［J］.振动与冲击，2011，30(3):252-257.

［4］ 陈国兴，陈磊，景立平，龙慧.地铁地下结构抗震分析并行计算显式与隐式算法比较［J］.铁道学报，2011，33(11):111-117.

［5］ 任强.基于ANSYS的某明挖地铁车站抗震分析［J］.现代商贸工业，2010，22(11):334-335.

［6］ 鲍鹏，盛桂琳.地铁车站抗震性能研究［J］.河南大学学报:自然科学版，2009，39(4):428-431.

［7］ 周爱红，袁颖，张鸿儒.基于ANSYS二次开发技术的土层随机地震反应分析［J］.煤炭学报，2007，32(11):1175-1178.

［8］ 赵岩，王德吉，张亚辉，林家浩.压电智能桁架随机动力特性研究［J］.机械科学与技术，2007，26(3):287-291.

［9］ 徐瑞，苏成.结构非平稳随机响应分析的快速虚拟激励法［J］.计算力学学报，2010，27(5):822-827.

［10］刘高，王秀伟.基于虚拟激励法的大跨桥梁抖振内力分析［J］.计算力学学报，2003，20(6):649-654.

［11］刘高，林家浩，王秀伟.考虑全桥耦合的大跨斜拉桥抖振内力分析［J］.大连理工大学学报，2003，43(4):479-483.

［12］阮松，冯美华.浅埋暗挖地铁站厅施工过程的三维数值模拟分析［J］.铁道标准设计，2009(10):65-68.

Analysis on Random Vibration Response of Metro Station Structure

MA Qian-ying1，LIU Zhi-qin2，WANG She-liang3，XIONG Er-gang1
(1.School of Civil Engineering，Chang'an Universit，Xi'an 710061，China;2.Department of Civil and Materials Engineering，Henan University of Urban Construction，Pingdingshan 467036，China;3.School of Civil Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China)

Considering the random uncertainty of seismic response，doing the structural seismic analysis by means of random vibration theory based on probabilistic method，and then investigating the dynamical reliability of structure，this method really is a reasonable method.This paper，after a random vibration analysis on Wusiguangchang Station of Qingdao Metro using pseudo excitation method，has avoided the tedious work of traditional calculation method，and has obtained dynamic response of the structure with statistical significance.When inputting the power spectrum along the X axis，the bending moment distribution is uniform relatively;the shearing force increases obviously at the change part of body form of the metro structure;the shearing force of the column bottom is relatively small，especially the shearing force of the column bottom of side span is less than that of middle span.When inputting the power spectrum along the Y axis，the shearing force increases gradually along the beam axis direction;the column bottom shearing force is bigger than that of inputting along the X axis;and the column bottom shearing force of the side span is bigger than that of middle span.The conclusion provides the basis for the reliability-based design of the complex structure like the metro station，functioning as reference for similar project design.

metro station;pseudo excitation method;random vibration

U231+.4

A

1004-2954(2013)09-0065-04

2013-03-12;

2013-03-17

国家自然科学基金项目(51208041，51178388，10972168，51108035);国家重点实验室开放项目(11JS061)。

马乾瑛(1982—)，男，讲师，博士，E-mail:mqianying@126.com。