基于效果的舰载软硬武器近卫火力分配研究*

解维河，吴从旭，汪德虎

(海军大连舰艇学院，辽宁 大连 116018)

水面舰艇驻泊、锚泊时，周围近区存在着如蛙人利用小型快艇和其它运载器等作战方式的威胁，此类目标发现突然、破坏威力大，一般采用多编组和多方向同时攻击，且作战形式不确定，对水面舰艇防卫造成很大困难。水面舰艇对该类近区目标防卫(以下统称为近卫)可以利用舰载的软硬杀伤性武器共同防卫，由于软硬杀伤武器作战性能的不同，对目标抗击包括毁伤、使其失能或者据止目标等多种效果。水面舰艇在遭受该类目标多方向威胁时，如何快速制定正确的软硬武器使用决策方案是能否进行有效抗击的关键，本文立足软硬武器对目标抗击效果，提出基于效果的水面舰艇软硬武器抗击近区目标的火力分配模型及解算方法，为水面舰艇近卫作战方案的制定提供有效的辅助决策方法。

1 水面舰艇近卫作战火力分配基本要求

1.1 发现目标突然，快速有效决策

近区出现的目标隐蔽性强，发现难度大，发现目标就要在短时间内进行快速决策予以抗击，因此，对近区目标防卫火力组织时间十分紧迫。使用什么武器、各武器对哪个目标进行抗击，需要在最短时间内决策出作战使用方案，才能为武器的使用提供充足的时间。

1.2 目标威胁不同，合理使用武器

水面舰艇近卫作战对象复杂，有些目标能够判断具有明显的攻击性，该类目标可能携带破坏威力较大的武器，要迅速利用武器进行有效毁伤。而有些目标威胁较小或不能直接判明是否对我水面舰艇具有攻击性，可以利用武器采取据止的方式使其脱离即可，因此，对近区目标防卫要针对目标威胁不同确定出作战效果，从而合理组织武器的使用方案。

2 水面舰艇近卫作战火力分配决策模型

2.1 问题说明

水面舰艇对近区出现的目标进行防卫配备软硬两种杀伤武器，在遇到近区目标威胁时，需要充分利用软硬武器对多个威胁目标进行抗击以达到最大的抗击效果。

对于同时出现的近区目标，进行火力分配是随着作战态势不断变化的，只针对一次抗击效果及火力分配进行研究，不考虑武器转火使用。

2.2 对目标抗击效果描述

使用软硬杀伤武器对目标的作战效果是不同的，利用硬杀伤武器可以对目标进行毁伤，而对于软杀伤武器，对目标不能够造成毁伤，其作战效果是对目标进行失能或者据止。

从对目标的总体作战效果来分析，可以将软硬杀伤武器对目标的抗击效果综合表述为毁伤失能或据止。

对于出现的n个近区作战目标，我水面舰艇利用软硬杀伤武器对任意第j个目标进行抗击的效果的概率可以表示为

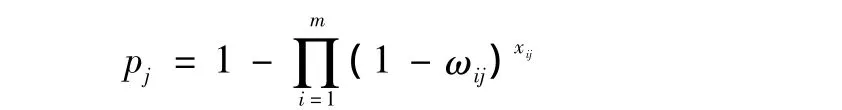
式中，pj为水面舰艇软硬杀伤武器对第j个目标达到毁伤失能或者据止的概率;xij为第i种武器抗击第j个目标的单位数;ωij为第i种武器的每个战斗单元(座)对第j个目标达到毁伤失能或据止概率，对短时间内每个战斗单元使用武器对目标的毁伤失能或据止可以认为是独立的事件。

2.3 目标函数建立

近卫作战对象主要是蛙人及其承载器，发现目标突发性强，且目标易损性强，对其作战要求在短时间内集中使用武器进行抗击，在一次抗击过程中，可以认为对各目标造成毁伤失能或据止过程中各武器使用效果是独立的事件，且分配给某个目标的武器作战效果对其它目标不构成影响，也认为是独立的，因此水面舰艇利用软硬结合武器对目标在一次抗击过程中所取得的总价值可以表述为

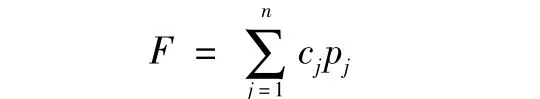
式中，F为水面舰艇利用软硬武器对近区目标作战效果的总价值;cj为第j个目标的对我水面舰艇的威胁程度;pj为第j个目标被软硬武器毁伤失能的概率或者第j个目标被软硬武器据止的概率。

建立软硬武器火力分配模型，实质是分别求得在取得毁伤失能或者据止近区目标两种作战效果情况下的总价值最大的武器分配方案，水面舰艇利用软硬武器对近区目标作战取得最佳作战效能的火力分配目标函数模型可以表示为

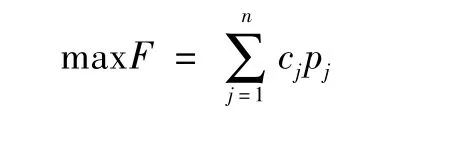
式中符号含义同上。

2.4 火力分配模型建立

依据上述分析，水面舰艇利用软硬武器对近区作战目标火力分配方案可以描述成如下形式:

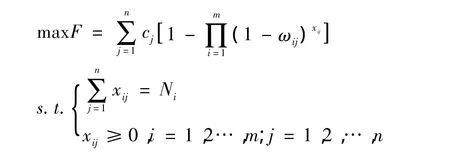
式中，Ni为第i种武器的数量单位;其它符号含义同上。该火力分配模型是一个有约束的非线性规划模型，可利用非线性规划方法求解。

3 水面舰艇近卫作战火力分配实例分析

3.1 战例想定

假设水面舰艇在近区突然发现3个不同方向的水面威胁目标，可用的武器有两座硬杀伤小口径火炮，三座软杀伤声光武器，由于目标威胁不同，对第二个目标达到据止的作战效果即可，对第一和第三个目标要进行毁伤或使其失能，要求在短时间内进行火力分配决策方案，并取得最大的抗击效果，为有效使用武器，对每个目标抗击的武器数量不超过2座，不考虑武器转火使用。

在研究近卫作战武器火力分配方法时，已知目标的威胁程度、武器的毁伤、失能以及据止的概率，可以通过敌我相对位置关系、目标的距离、速度以及我舰软硬武器的战技性能计算出来。假定该时刻确定出目标对我水面舰艇的威胁程度及各武器的作战效果概率，见表1所示。

表1 目标的威胁程度、武器的毁伤概率

3.2 模型建立

每座武器作为一个火力单位，不考虑转火，一座武器只能针对一个目标攻击;而为有效使用武器，要求对每个目标抗击的武器数量不超过2座，可以将每个目标虚拟成2个，这样就可以保证每个目标抗击的火力单位不超过1个，可以表示成一对一的火力分配问题。

即共有软硬武器共有5个火力单位，对6个目标攻击，将武器依次排序，前2个为硬杀伤武器，后3个为软杀伤武器，即将问题转化成m=5，n=6的火力分配模型:

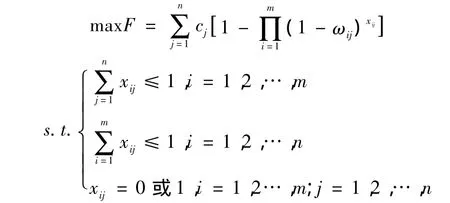
式中，ωij为第i座武器对目标j毁伤概率。其中，

3.3 基于匈牙利算法的模型解算

按照文献［3］，将上述模型转化为能够运用匈牙利算法解算的模型。因为m＜n，虚拟一个火力单位，得到n=6的火力分配模型:

系数矩阵为

在矩阵R上运用匈牙利算法，可以得到一个最优矩阵:

最优矩阵中最优值对应项即为各武器对不同目标的抗击方案，即火力分配的最优方案是:对第一个目标，采用一座硬杀伤武器和一座软杀伤武器进行抗击;对第二个目标，采用一座硬杀伤武器进行抗击;对第三个目标，采用两座软杀伤武器进行抗击。

采用上述火力分配方案，水面舰艇软硬结合武器该时刻对该批次目标抗击效果的效能指标值为

3.4 结果分析

火力分配结果确定出了某时刻对基于不同效果的目标作战的火力分配方法，在进行火力分配时，需要确定出对某次作战需要取得的作战效果，同时如果将目标的威胁程度、武器的毁伤、失能以及据止的概率等因素时时计算出来作为输入量，可以确定出不同时刻的武器使用火力分配方案。

在作战决策过程中，根据不同目标可以确定相同的抗击效果，对于同一目标在不同威胁程度下也可以确定不同的抗击效果。在进行火力决策方案时，可以依据取得相同的作战效果来进行火力分配，也可对每个目标确定不同的作战效果来进行火力分配，对于模型的解算来说只是其输入的抗击效果概率不同，可以将武器的威胁程度、抗击概率等模型加入到火力分配模型中，以增强火力分配方案制定的实效性。

火力分配方案的结果可以有多个，各最优方案抗击效果指标结果是一样的，对不同威胁情况下每种武器的取得抗击效果越为准确，其方案越符合实战要求，同时，抗击效果的概率确定得越为准确，方案的结果也越精确。

4 结束语

本文根据水面舰艇对近区目标防卫作战火力分配研究需求，建立水面舰艇利用软硬结合武器作战火力分配模型，并通过实例对模型进行仿真，研究模型的解算方法，所建立的模型及算法对水面舰艇近卫作战火力辅助决策的研究具有一定的意义，在模型和方法使用的界限和工程实现等方面还需进一步研究。

［1］唐焕文，等.实用最优化方法［M］.大连:大连理工大学出版社，2010.

［2］金钊，原超，朱传伟.编队舰空导弹火力分配中的通道组织问题研究［J］.战术导弹技术，2011(6):39-43.

［3］黄力伟，等.基于匈牙利算法解算的火力分配问题［J］.海军大连舰艇学院学报，2010(8).

［4］冯杰，等.数学建模原理与案例［M］.北京:科学出版社，2007.

［5］肖华勇，等.实用数学建模与软件应用［M］.西安:西北工业大学出版社，2008.

［6］张华燕，等.军事激光技术［M］.北京:国防工业出版社，2011.