基于仿真实验的弹道导弹阵地优选*

曹志华，胡晓峰，张兆栋

(1.国防大学信息作战与指挥训练教研部，北京 100091;2.解放军66347部队，河北 保定 071000)

弹道导弹攻防对抗已成为现代体系对抗的重要内容之一。弹道导弹阵地选择是作战规划的重要环节，直接影响弹道导弹的突防概率、作战效能等。影响弹道导弹阵地选址的因素较多，除地形、天候、装备性能等，对方防御系统的配置方式、预打击目标的方位、预期打击效果等都制约着发射阵地的选择。

传统的发射阵地选择方法主要采用解析计算的方式，如黄锐等提出的基于BP神经网络的导弹阵地选择评估方法［1］，文献［2-3］在层次分析法的基础上提出基于DS/AHP和基于Fuzzy-AHP导弹发射阵地选择方法，宋昭峰等提出的基于模糊指派的阵地选址决策［4］。这些方法思路清晰、方法简便，但一些关键参数的选择主要依靠专家经验，带有较强的主观性，是一种静态、非对抗条件下的分析方法，在描述不确定性因素对阵地选择的影响方面存在“天生”缺陷。本文将解析法与仿真实验相结合，研究弹道导弹阵地选择问题。

1 弹道导弹攻防对抗的博弈过程

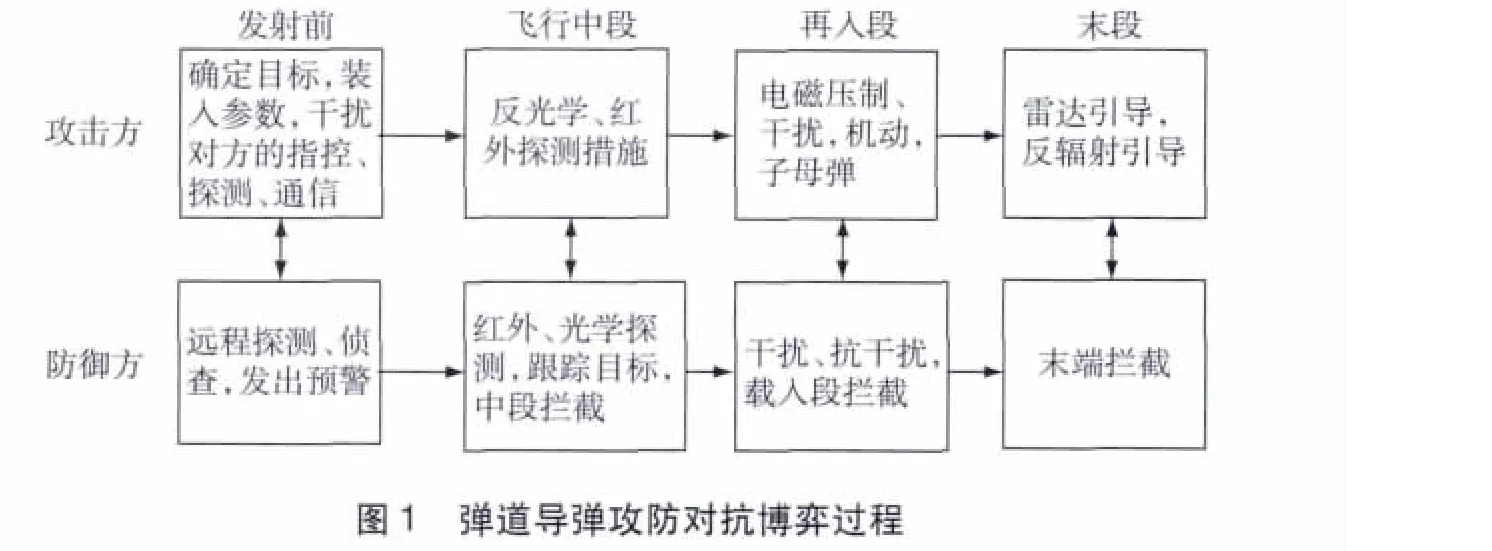
弹道导弹的攻防对抗，是攻击方所采取的以信息战和弹头机动为主的突防措施和防御方采取的探测、捕获、识别跟踪、诱导、干扰、拦截行动之间的斗争，这种斗争贯穿于整个攻防作战过程［7，12］，见图 1。

2 仿真实验框架

2.1 系统结构

弹道导弹阵地优选仿真以体系对抗条件下的弹道导弹攻防对抗为军事背景，在现有武器装备效能评估平台的基础上，对进攻作战、防御作战等各种作战行动以及作战实体进行建模并将其聚合为弹道导弹攻防对抗仿真模型。具体结构见图2。

仿真引擎主要由仿真运行支撑环境和各类模型组成，是整个仿真环境的核心，模拟指挥控制决策过程、航迹处理、消息处理，以及想定中所有平台的作战与武器运用过程的模拟。

实验设计模块主要用于完成编辑作战想定，包括双方作战编程、作战部署、武器装备参数设置等，设定实验运行条件(如随机种子、蒙特卡洛运行次数)等。

数据管理是存储、处理实验运行中产生的中间数据和结果数据，用来进行可视化分析和各种统计分析。

结果分析模块主要是对仿真数据进行分析和处理，得出评估结论，支持可视化分析、仿真数据回放、统计分析。

2.2 对于作战实体和主要作战行动的建模

模型系统采用EBI建模框架，通过实体、行为、交互、效能评估、作战规则的建模，实现对弹道导弹攻防对抗的仿真模拟，反映导弹飞行、预警、识别、拦截、毁伤等整个作战过程，主要有以下四个模型。

·导弹发射单元模型以及弹头武器模型 发射单元模型通过作战规则描述了弹道导弹作战单元的作战行为，分为固定式和机动式。固定式描述了导弹发射与被拦截阶段的行为，机动式作战单元在描述发射和拦截行为的基础上，又增加了架设、重装弹药等作战行为的刻画和描述。武器模型通过统一的武器定义方式来定义不同类型的弹头，通过参数的搭配定义不同类型的弹头，通过杀伤概率表来描述的弹头对不同目标的杀伤概率，从而体现不同弹头的特殊性。

·传感探测模型 包括雷达个体建模和传感器网络建模。雷达个体建模侧重于雷达在复杂电磁环境下探测、测量、跟踪等工作过程的建模，并形成目标航迹。雷达个体建模包括预警、火控、指挥引导等。传感器网络建模是在雷达个体基础上，对雷达个体之间航迹传输以及航迹融合的建模，形成更为准确、全面的目标信息，用于态势感知、信息优势分析等。

·指挥控制模型 主要有目标识别模型、威胁评估和目标选择模型、发射数量决策模型、临机响应模型。在指控网络模型方面，建立信息融合模型、协同作战模型、冲突消解模型。

·通信模型 主要有通信网络、通信节点、通信路径、消息、通信协议等实体模型，刻画作战过程中信息产生、传输、处理、分发的信息流程。

2.3 仿真实验流程

仿真实验的具体流程如图3，具体描述如下:

Step1:通过专用想定定义工具建立仿真想定，包括对每个作战实体的属性进行设定、作战环境设置、仿真运行条件设置等;

Step2:运行想定，对所有作战实体按照仿真步长推进其作战事件并修改其状态，对于涉及概率的作战事件的结果通过蒙特卡洛方法确定事件结果，记录仿真过程中产生的各种交战数据;

Step3:设置分析条件，对仿真结果进行可视化分析;

Step4:判断是否仍需分析，如果否，则结束该过程，否则，修改想定，返回Step1。

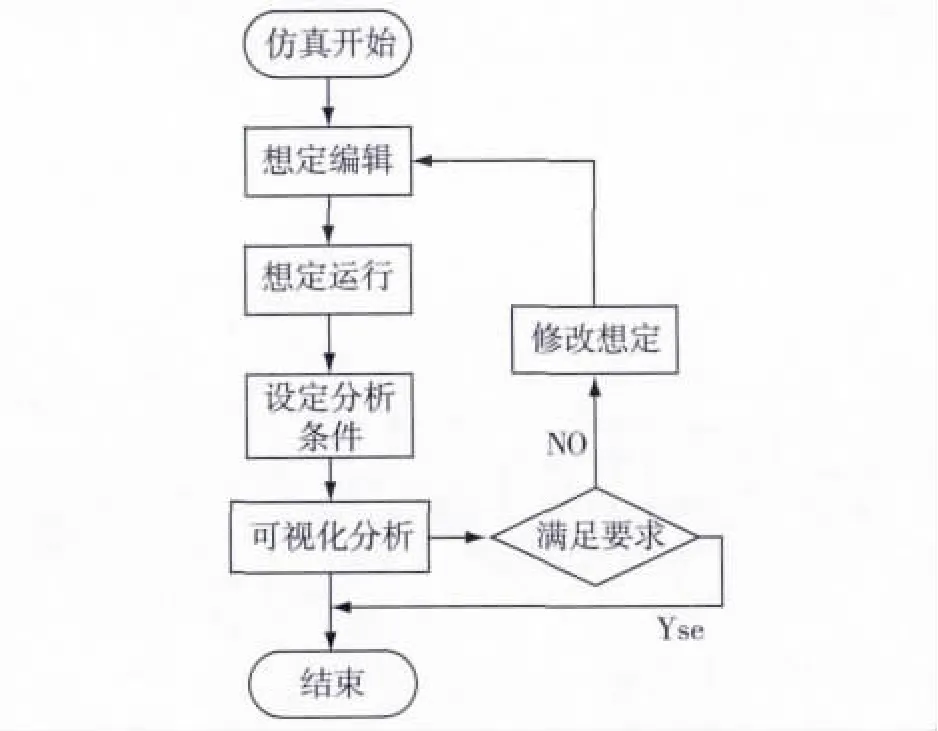
图3 仿真实验的基本流程

2.4 仿真运行模式的优化［5］

传统军事仿真一般采用蒙特卡洛运行模式，当目标的毁伤概率超过一定阈值即认为目标已被摧毁，退出仿真，并通过多次蒙特卡洛仿真对结果进行统计分析。弹道导弹攻防对抗是侦查与反侦查、预警与反预警、突防与拦截等一系列相关联的复杂对抗活动，各种因素的不确定性会形成巨大的想定空间，如果采用蒙特卡洛运行方式，需要运行想定空间的每一个想定，然后对运行结果进行综合分析，其运算量无疑是巨大的。因此，本文对仿真模型的运行模式进行了优化。模型运行时，双方的武器弹药没有限制，导弹会按计划攻击每一个预定目标，防御方也会按照规则进行拦截。运行过程中系统自动收集防御方对进攻方的毁伤概率和交战位置信息，同时也会收集进攻方对防御方的毁伤概率和交战信息。这种运行模式仅仅通过单次想定运行就能收集到所有数据，而传统模式，需要经过多次蒙特卡洛仿真运行才能做到这一点。因此，大大减少了仿真运行次数，提高了仿真运行效率。

2.5 仿真结果的可视化

实验结果分析是仿真实验分析过程的最后一个步骤，整个过程可以概括为基于结果数据，通过各种分析手段寻找所关心问题的答案。常用的分析方法有统计分析、数据挖掘、仿真结果的OLAP等［6］，本文采用计算机可视化的方法，将仿真结果数据以图形图像的方式输出，具有清晰、直观的特点，有助于决策人员进行快速分析。

2.6 仿真实验的边界条件

在能够说明问题的前提下，本文对实验作了如下假设。

1)进攻一方的导弹有最大最小射程的限制，在它的攻击范围内，可以以一定概率攻击任何类型的目标。这种概率由导弹类型、目标类型、两者之间的距离等因素综合决定。

2)导弹一旦发射就会被防御方的各种传感器探测到，并提供跟踪预警，则导弹攻击的突然性为零。

3)如果导弹在飞行过程中没有被拦截，那么它命中且毁伤目标的概率为100%，即ka=1。

4)拦截器命中来袭导弹后，导弹不再具有破坏效力，不考虑爆炸、核、生、化等带来二次危害。

5)攻击方所使用的导弹都是单弹头，且不具有末端机动能力。

6)打击目标可以是一个点目标或者面目标，可以根据需要灵活确定。由于只有一个目标，可将目标价值valuet设为1。

7)把可配置地域均匀划分为m×n的网格(视需求而定)，将网格的交叉点作为防御平台的候选配置位置，这样可供选择的位置就有m×n个，如图4所示。

8)不考虑复杂电磁环境(电磁干扰等)对双方武器装备性能的影响。

3 仿真实验的数学模型

3.1 弹道导弹阵地部署的准则

科学合理的部署有利于弹道导弹突破对方的防空反导系统，增加导弹命中目标的概率，提升体系对抗效能，从而形成有利于己、不利于敌的战斗态势。对于攻击方而言，其目标是选择适当配置，以获得总体上的最大期望杀伤效果。因此，弹道导弹阵地优选问题可以归结为:选取合适的火力，配置在适当的位置，取得最大的效能。

3.2 非对抗条件下弹道导弹作战效能评估模型［7］

对于攻击方来讲，攻击效能一般与打击目标可接受的风险和弹道导弹的毁伤水平有关。但是这种方法的有效性测量很难实现，因此一般将漏截概率和目标价值作为效能评价指标，弹道导弹的打击效能可以表示为:

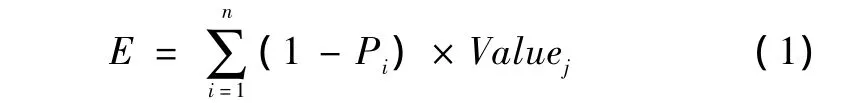
其中，E表示系统效能，P表示漏截概率，Value表示防御目标的价值，n表示导弹数量。同样地，可以得出防御系统的防御效能为:

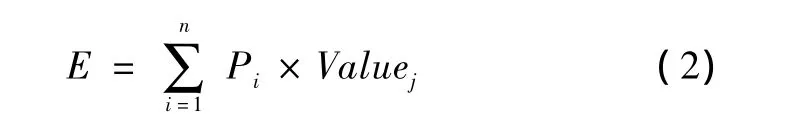
3.3 体系对抗条件下弹道导弹作战效能评估模型

根据本文的作战效能模型，联立进攻方和防御方的目标函数，并对模型进行扩展，建立对抗条件下弹道导弹作战效能的评估模型(min-max模型)如下［8］:

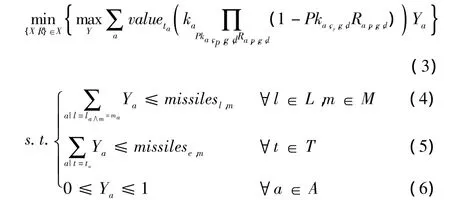
模型中的符号及变量的含义如下:l∈L表示弹道导弹的发射点位置及其集合;m∈M表示弹道导弹的类型及其集合;t∈T表示弹道导弹攻击的目标及其集合;a∈A表示攻击行动及其集合;la表示从位置l发起的行动a，la∈a;ma表示使用类型为m的导弹的攻击行动，ma∈M;ta表示目标为t的攻击行动a;p∈P表示防御平台及其集合;c∈C表示防御平台的类型及其集合;cp表示类型为c防御平台p;g∈G表示防御平台的部署位置及其集合;i∈I表示拦截器的类型及其集合;d∈D表示防御行动及其集合;相关变量及含义:missilel，m表示类型为m，位于l的导弹;valueta表示目标的价值;ka表示攻击毁伤目标ta的概率;max-missilest表示攻击目标t的弹道导弹的最大数量;loadoutc，i表示类型为 c 的平台发射 i类型的拦截器;salvoa，c，d，i表示针对进攻方的行动a，防御方使用类型为c的防御平台，采取防御策略d，发射拦截弹类型为i的拦截弹的数量;Pka，c，g，d表示对于某次打击行动 a，预先部署在 g 的类型为c的平台，发射类型i的拦截弹对其进行拦截的成功概率;Ya二进制变量，1表示行动a发生，0表示其他;Xp，g二进制变量，1表示平台p部署于g，0表示其他;Ra，p，g，d二进制变量，1 表示部署于g 的防御平台对进攻a采取防御行动d。

其中，式(3)为模型的目标函数，该式描述了攻击方在防御部署已知的情况下所获得的最大期望杀伤效果;式(4)表示发射位置对导弹数量的约束;式(5)式示对每个目标的最大可用弹道导弹数量的约束;式(6)表示行动约束，即一枚导弹攻击一个目标。

防御行动的约束条件{X，R}∈X如下:

式(7)表示一个防御平台只能部署在一个位置;式(8)表示每个栅格位置只能部署一个火力平台;(9)式表示对于每次攻击最多进行一次拦截;式(10)表示每个栅格出的火力平台的作战任务数量;式(11)、(12)为二元决策变量。

min-max模型的求解方法，主要有两种:一是根据线型规划对偶原理，把min-max问题化为min-min问题，二是根据bender分解原理，分解成2个子问题进行求解［9］。虽然效率较高，却难以描述评估对象与环境之间复杂的关联，评估结果不太精确，而仿真实验法可以充分描述实体与实体、实体与环境之间的相互作用、相互依赖关系，并将这些相互关联的影响通过多次随机仿真涌现出来［10］。

4 示例及结果分析

4.1 基本想定

本文以1对1分析(One-on-One Analysis)为例［11］，假设红蓝双方之间进行弹道导弹攻防对抗，红方为攻击方，蓝方为防御方。现已知，蓝方某类型防御平台部署于某固定位置，红方某弹道导弹发射平台配置地域不定(对抗双方态势见图4)，对蓝方某一固定目标进行打击，通过仿真进行优化部署的目的就是确定弹道导弹阵地的最佳部署区域。

4.2 仿真结果分析

图4为弹道导弹CEP为500m，命中目标概率为0.5，防御系统拦截的最远距离为200km，拦截概率为0.8，弹道导弹毁伤门限为 0.9时的结果(超过 0.9 认为弹道被拦截并失去破坏效力)。

从实验结果可以看出，对于红方来讲，最差的部署方案是将导弹发射阵地部署在上方区域，发射出的导弹被对方拦截的概率最高，为0.95以上，其次是部署在拦截概率为0.50和0.30的区域。部署在其他区域的导弹的突防概率最大，是理想的配置地域。

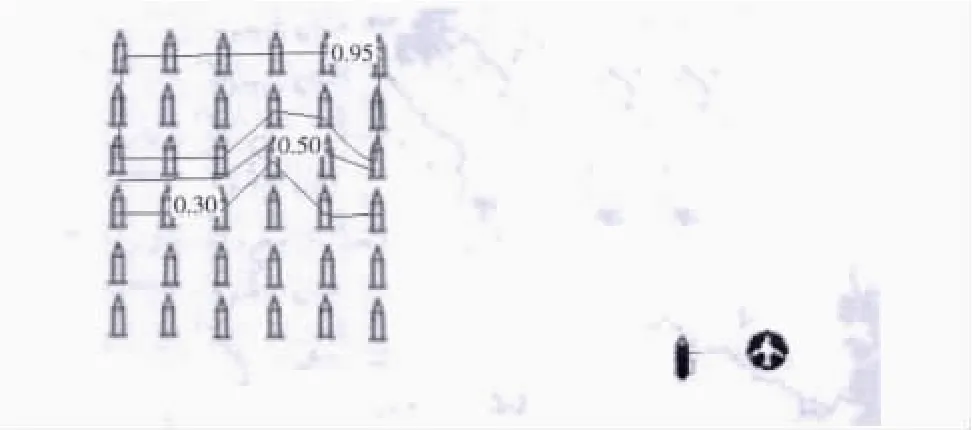
图4 1对1分析的仿真结果

4.3 其它情况

图5-6是在上述基本想定的基础上，蓝方增加一个防御平台之后的仿真结果。通过对比可以看出，蓝方在增加防御系统配置之后，对红方的影响比较大，导致红方的可选配置地域大大缩小，如图5所示。在防御方增加防御平台之后，红方导弹命中目标概率大于50%的可选阵地数量由28个降低到10个，命中目标大于70%的可选阵地数量由13个降低到5个，见图6，表明防御方反导平台数量的增加，对导弹阵地选择影响较大，会大大限制阵地的选择范围。该结果对实际作战指挥也具有一定指导意义:在多波次火力打击时，要想最大限度发挥弹道导弹突击效果，应考虑首先摧毁对方的防御平台。

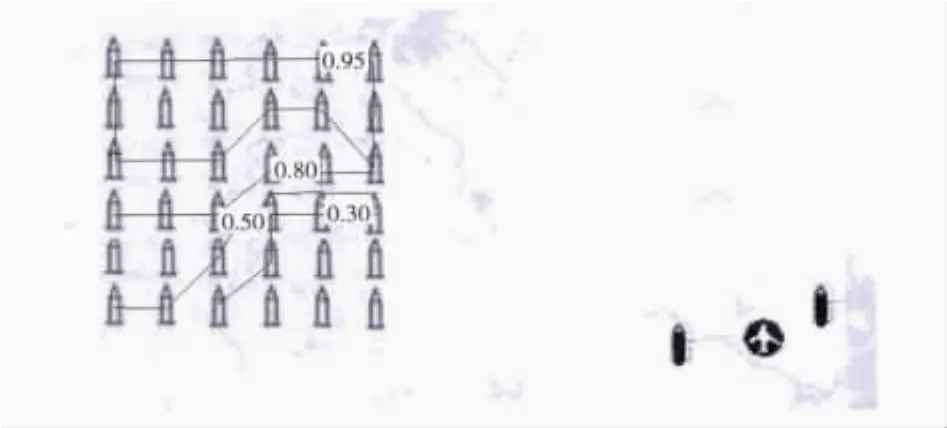
图5 1对2分析的仿真结果1

5 结束语

弹道导弹阵地优选问题是一个动态非协同的博弈过程，传统的方法难以反应“动态”、“对抗”特征。本文将解析法与仿真实验相结合，克服了以上不足，首先构建弹道导弹攻防对抗的仿真模型，然后通过仿真实验来探寻弹道导弹的最优配置阵地。示例表明，利用该方法可以快速得到弹道导弹阵地的最优部署区域，结果清晰、直观。且实验中通过改进仿真运行模式，大大减少了实验次数，提高了实验运行效率。但该模型没有考虑复杂电磁环境对双方武器装备的影响，构建的弹道导弹模型还不够精细，对诸如分导式多弹头弹道导弹、具有末端机动能力的弹道导弹还不能进行仿真模拟。

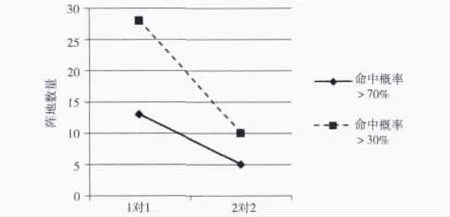
图6 1对2分析的仿真结果2

［1］黄锐，毕义明，张信启.基于BP神经网络的导弹阵地选择评估［J］.四川兵工学报，2009，30(6):56-63.

［2］刘顺成，刘卫东.基于DS/AHP的导弹发射阵地选择方法［J］.指挥控制与仿真，2007(5).

［3］吴晓露等.基于Fuzzy-AHP的导弹发射阵地评估方法［J］.信息系统工程，2009，10(1):52-55.

［4］宋昭峰，刘付显.基于模糊指派的阵地选址决策［J］.火力指挥与控制，2006，31(7):34-36.

［5］张明智，邓晶.基于使命模式的仿真想定动态提炼研究［J］.系统仿真学报，2012，23(7).

［6］胡剑文，等.作战仿真实验设计与分析［M］.北京:国防工业出版社，2010.

［7］罗小明，等.弹道导弹攻防对抗的建模与仿真［M］.北京:国防工业出版社，2009.

［8］Diehl D Diehl.How to Optimize Joint Theater Ballistic Missile Defense［D］.California，Naval Postgraduate Schoo1，2004.

［9］周晓光，李为民，谢鑫.多层反导体系火力部署优化［J］.空军工程大学学报，2011，12(3):40-44.

［10］杨镜宇，司光亚，胡晓峰.信息化战争体系对抗仿真分析方法研究［J］.系统仿真学报，2005，6(17):1469-1472.

［11］Wayne J.Pavalko，Kanaya R.Chevli，Michael F.Monitus.Theater Ballistic Missile Defense Analyses［R］.Johns Hopkins APL Technical Digest，Volume 21，NUMBER 2(2000).

［12］幺飞，赵春晖.弹道导弹攻防效果评估仿真研究［J］.指挥控制与仿真，2010，32(2):73-77.