IMF复杂度特征在心音信号分类识别中的应用

郭兴明，黄林洲

GUO Xingming,HUANG Linzhou

重庆大学 生物工程学院，重庆市医疗电子技术工程研究中心，重庆 400030

College of Bioengineering,Chongqing Engineering Research Center for Medical Electronics Technology,Chongqing University,Chongqing 400030,China

心音识别一直是心音分析诊断领域难度较大的研究课题，旨在根据不同心音信号特征来判定所属疾病类型。Yoganathan通过快速傅里叶变换对心音进行分析发现，由于生理、病理或者自然环境的影响，心音信号常表现为非线性、非平稳特性[1]。目前，常用心音信号分析[2-3]和特征提取方法[4-5]主要从时域、频域、时频域联合分析，具体表现为：时域分析提取心音信号的包络；频域分析得到心音频率成分和功率谱信息；通过小波、小波包、希-黄变换等方法对信号进行时-频分析，获取时间和频率的联合函数来量化心音信号。总结比较上述方法，其本质上都存在线性稳态缺陷，心音分析过程不是自适应的，不能准确量化心音信号非线性、非平稳性本质特征。而Kumar等对心音各频段的混沌分析表明：心音的非线性特征分量比线性特征分量具有更好的特异性，有利于心音识别[6]。

经验模式分解（Empirical Mode Decomposition，EMD）是一种新的信号自适应分析方法，可根据信号的局部时变性将信号分解成多个平的固有模态函数（Intrinsic Mode Function，IMF），从而减少信号特征信息的干涉或耦合，利于深层次信息挖掘。故利用EMD对心音信号进行分解，再从IMF分量中提取特征信息（如瞬时频率、关联维数等）更能反映心音的本质。复杂度是反映时间序列随长度的增加出现新模式的速度，能够定量反映系统状态变换情况，广泛地用于肌电信号模式识别[7]、共振特征描述[8]和脑电特征分析[9]等领域。复杂度对系统的状态变化敏感，故有利于特征的提取。

本文采用EMD方法将非平稳心音信号分解成若干平稳的IMF分量，并利用互相关系数准则去除噪声和虚假分量，计算所筛选IMF分量的非线性复杂度值，实现心音信号特征向量的有效提取，然后利用BT-SVM实现病理心音识别。最后以临床采集的数据为例，验证了该方法的有效性。

1 基本原理与算法

1.1 EMD算法

EMD是Huang等人在总结了瞬时频率有实际物理意义的分量应满足条件的基础上，提出的一种能将非平稳的信号分解成若干平稳IMF分量的信号处理方法。其算法如下：

步骤1确定原始信号x(t)的局部极值点，通过三次样条函数拟合出上包络线和下包络线umax(t)和umin(t)，得到其局部均值s(t)。

步骤2计算差值h(t)=x(t)-s(t)，如h(t)不满足IMF的条件，即h(t)为新的原始信号，重复步骤1，直到hk(t)满足IMF的条件为止。

K值由循环终止阈值标准差SD决定。

其中，N为序列的长度，SD因不同长度、不同性质的信号决定。

步骤3得到第一个IMF分量C1=h1k(t)和余项R1(t)。

步骤4将R1(t)作为新的原始信号，重复步骤1～3，得到所有IMF为C1，C2，…，Cn直到Rn(t)基本呈单调趋势或者|Rn(t)|趋于零时停止，此时原始信号x(t)可表示为：

式中Ci(t)为第i个IMF分量，Rn(t)为残余分量。

1.2 复杂度算法

LZ复杂度是Lemple和Ziv提出的一种度量非线性序列复杂程度的方法，非常适用于时间序列的非线性复杂度特征提取。为提高算法实效性，先对信号进行二值化，设某序列 P=S1，S2，…，Sn，定义P序列的子序列 S、Q和S、Q的合并序列SQ。SQ_min us是将SQ的合并序列的最后一个元素删除后剩余的序列。其算法如下：

步骤1初始化，设定复杂度c(n)=1，S=S1，Q=S2，SQ=S1S2，R=S1。

步骤2判断Q是否是SQ_min us的子集，若是，转步骤3，若不是，转步骤4。

步骤3 c(n)不变，S不变，Q往后多取一位，继续步骤2。

步骤4 c(n)=c(n)+1，SQ作为新的S，SQ后的第一个字符作为新的Q，继续步骤2，直到Q取到最后，此时的c(n)值为该段序列的复杂度。进而计算其相对复杂度C(n)，即C(n)=(c(n)×lb n)/n。

可见，LZ复杂度值反映了序列随长度增加而产生新模式的速度，即序列复杂度越大，产生新变化的速率越大，表明数据变化是无序复杂的。反之，复杂度越小，则说明产生新变化的速率越慢，数据变化是趋于规律的。因此，复杂度能描述出序列的变化特性，可作为信号系统的状态的特征参数。

1.3 支持向量机

SVM源于Vapnik提出用于解决模式识别问题的机器学习方法，基本思想[10]是根据结构风险的最小化原则，在拉格朗日乘子和最优化条件（Karush-Kuhn-Tucker，KKT）下，先使用内积函数定义的非线性变换将输入空间变换到一个高维空间，然后在这个空间中构建独立的最优超平面。其分类函数为：

其中，sign为符号函数，w为分类超平面法向量，K(x，xi)为核函数，b为最优超平面的位置。

相对于非线性函数逼近方法，SVM具有更强的泛化能力，并克服了神经网络中网络结构难以确定和不可避免的局部最小值问题，具有解决小样本，高维模式识别问题的优势，近年来被广泛用于分类、函数逼近和时间序列预测等方面[11-13]。

SVM主要针对2分类情况，而现实中往往需进行多类型识别，因此先需要将多类转化为两种分类问题。通常采用组合分类器方式来实现，主要有一对多、一对一、决策导向无环图等，但它们都有一定的不足[14]。目前，二叉树SVM应用较多，它不仅克服了不可分问题，对k类问题只需要构造k-1个2类分类器，且重复训练样本少，从而节省训练和测试时间。因此，本文选用此方法。

2 基于IMF复杂度特征和BT-SVM的心音识别方法

本文先对心音信号进行EMD分解，得到若干IMF分量，并利用互相关系数准则对其筛选，计算所筛选IMF分量的非线性复杂度值，并组成特征向量输入至BT-SVM进行心音的分类识别，如图1所示。

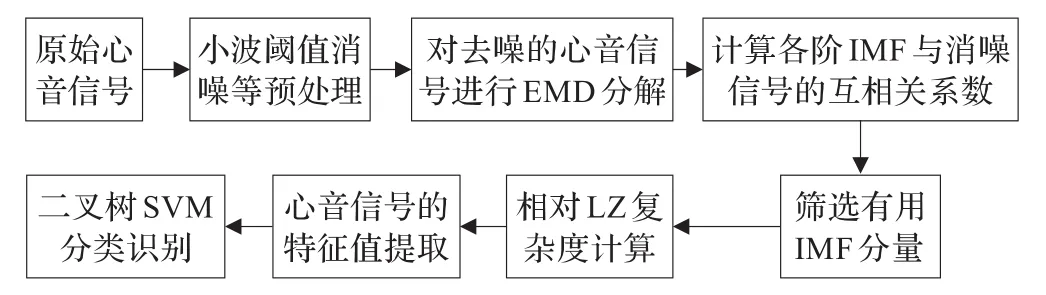
图1 EMD复杂度结合SVM的心音识别示意图

具体步骤如下：

（1）由于心音临床采集过程中不可避免地引入噪声，为有效提取心音特征，首先使用小波阈值法去除噪声，以减少EMD分解次数，从而减少由于多次分解带来的端点效应累积误差。

（2）对经过消噪的心音信号进行EMD分解，得到若干IMF和余项。通过对IMF分量的特征提取就可以得到原信号的特征。

（3）不同的心音信号EMD分解后会得到不同个数的IMF，由于噪声和虚假分量的存在，故需对其进行筛选。根据概率统计中互相关系数概念，各IMF分量与原心音信号的相关性较大，而噪声分量和虚假分量与原心音信号的相关性很小。因此，计算各IMF分量与原信号的互相关系数对真实IMF进行筛选。

（4）计算筛选后真实IMF分量的LZ复杂度值为信号的非线性复杂度特征，然后将其组成特征向量，输入到BT-SVM进行心音分类识别。

3 实验及分析3.1 实验数据

采用重庆博精医学信息研究所研制的“运动心力监测仪”（ECCM，专利号01256971.2，第一代产品注册证号：渝药管械（试）字99第220007）在重庆医科大学附属医院采集的心音样本来验证该方法的有效性。包括19例二尖瓣狭窄（MS）、15例主动脉瓣狭窄（AS）、14例室间隔缺损（VSD）和48例正常心音（NHS）。记录数据时，将心音传感器置于受试者心尖区，同时要求受试者保持匀速，平静呼吸，采样频率是11.025 kHz，量化值为8 bit，采集的信号最终以wav格式进行保存。全部病理数据都是经过专家确诊的单一性病例，健康人群均无心血管和家族病史。

3.2 心音信号预处理

由于心音采集时不可避免地引入各种噪声，本文采用时间局部性好，能量集中度高的db7小波和基于Stein无偏似然估计的rigrsure阈值方法对临床采集的心音信号进行消噪。图2为一例消噪前的正常心音信号。

图2 原始的心音信号和db7小波消噪对比

由图2可知，此消噪方法能较好地保留心音主要成分，减少毛刺等高频信号对波形的干扰，滤波效果较好，利于特征参数提取。

3.3 心音信号特征提取

对预处理后的心音信号进行EMD分解，得到n阶IMF分量Ci(t)(i=1，2，…，n)。图3表示为一例消噪后的正常心音信号EMD分解。

图3 正常心音信号EMD分解结果

从图3可见，EMD把非平稳的正常心音信号分解成了11个IMF分量和1个残余分量，不同的IMF分量包含了不同的时间尺度。用互相关准则计算各IMF分量与原始信号的互相关系数，分析多次平均后的计算结果表明IMF2～IMF6分量与原始心音信号的相关性较大，其他高阶IMF分量与原始心音信号的互相关系数皆在0.01或更小的数量级。因此分别对上述三种异常病理信号和正常信号进行EMD分解，并计算原信号和IMF2～IMF6分量的LZ复杂度，如表1所示，然后选用IMF2～IMF6分量的LZ复杂度值作为SVM的输入特征向量记为 X=(X1，X2，X3，X4，X5)。

由表1可知，EMD分解后每阶IMF分量的LZ复杂度不同且各具特点，从而揭示各自的本质特征和不同非线性产生机理，随着分解层数的增加，LZ复杂度呈递减趋势，反映了非平稳信号EMD分解本质。相比三类异常病理信号，正常信号的复杂度值最低，说明相对于正常的心音信号，异常病理信号较复杂，表明其非线性非平稳性更强。

3.4 SVM识别网络

针对3类病理心音在内的四种心音样本，建立3个BTSVM，按最优分类函数进行分类，如图4分类流程图所示，组成四种状态的多分类支持向量机。

在选择SVM进行状态识别时，核函数的好坏直接影响分类器的性能。本实验选取径向基核函数（Radial Basic Function，RBF），因为其更符合特征提取的要求，即不同类别样本在特征空间的距离尽可能大，同一类别样本间距离尽可能小。径向基核函数有两个参数Gamma和惩罚因子C，其大小决定了模型的复杂性和训练误差。为得到最优的分类器，本文使用舍一交叉验证法[15]（n-fold cross validation）确定两参数Gamma和惩罚因子C，对于给定的每一个参数对（Gamma，C），均进行10次交叉验证，在Matlab中选择svmtrain函数对训练集分割成10份，其中的9份作为训练集，剩下的1份做测试集，将每次测试的结果取平均值作为该参数对的指标，最后选择指标最高的一组参数对作为最终的最优参数。经确定（Gamma，C）为（2，2）时的分类准确率最高。

表1 信号及IMF复杂度分布

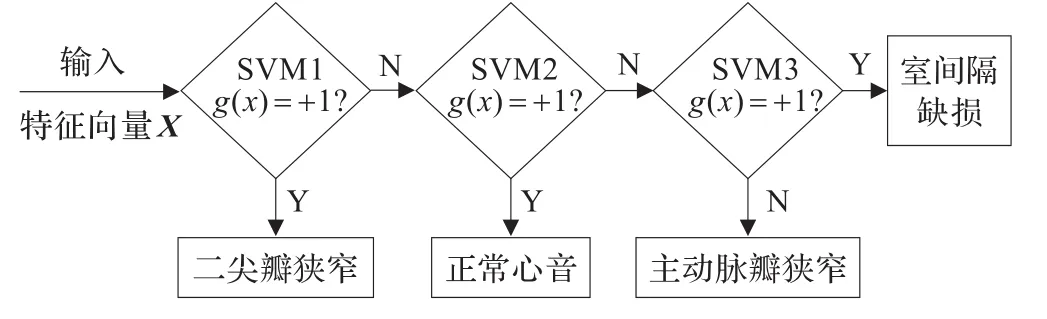
图4 BT-SVM分类流程图

4 实验结果与讨论

为比较SVM和常用识别网络识别效果，按不同的数量样本（训练集样本∶测试集样本）测试其性能，结果如表2所示。实验硬件平台为戴尔Precision T7500，CPU为Xeon X5670，主频 2.93 GHz，内存为 ECC DDR3，大小为 4 GB。软件平台为Microsoft Windows XP下的Matlab7.1版本，算法运行时间通过Matlab中提供的“tic、toc”获得。

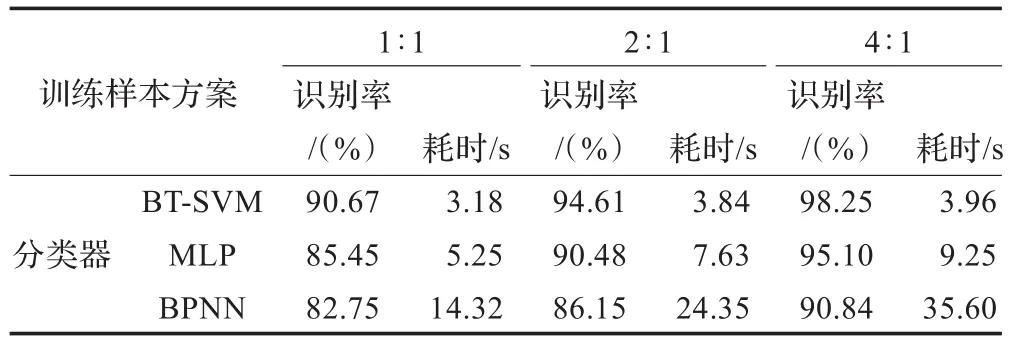
表2 不同分类器识别结果对比图

由表2可知，无论在耗时还是识别率上，SVM都具有很大的优势，特别是训练样本较少时表现出了高识别率。另外，当使用BP神经网络时发现，当误差指标是0.01时，训练样本方案选择4∶1时其识别率为90.84%，但同样当误差指标为0.05时，分类准确率为82.75%，这说明此时BP神经网络已经出现过学习的情况。

5 结束语

心音信号是一种高度非线性、非平稳信号，本文提出一种基于IMF复杂度和BT-SVM的心音分类识别方法。临床试验数据仿真表明，EMD能将非平稳信号自适应分解成平稳的IMF分量，从而突出心音的局部特征。非线性LZ复杂度值反映了不同尺度下心音信号变化的不规则性和复杂性，从而有效提取心音特征，为分类识别提供依据。相比传统的识别网络，BT-SVM较好地节省了训练时间，从而快速有效地实现心音信号识别。因此，该方法能有效地提高非线性、非平稳心音信号特征提取的准确性和分类识别的高效性，对进一步实现心脏疾病的无创诊断具有重要的参考价值。

[1]Yoganathan.Use of fast fourier transform for frequency analysis of the first heart sound in normal man[J].Med Biol Eng，1976，14：69-72.

[2]张国华，袁中凡，李彬彬.心音信号特征提取小波包算法研究[J].振动与冲击，2008，27（7）：47-49.

[3]Rakovic，Sejdic E，Stankovic L J，et al.Time-frequeceny signal processing approaches with applications to heart sound analysis[J].Computers in Cardiology，2006，33：197-200.

[4]Debbal S M，Bereksi-Reguig F.Computerized heart sounds analysis[J].Computers in Biology and Medicine，2008，38：263-280.

[5]Maglogiannis，Loukis，Zafiropoulo.Support vectors machine based identification of heart valve diseases using heart sounds[J].Computer Methods and Programs in Biomedical，2009，95（1）：47-61.

[6]Kumar，Carvalho P，Antune S M.Discrimination of heart sounds using choas analysis in various subbands[C]//Proc of the 2nd International Conference on Bio-inspired Systems and Signal Processing BIOSIGNALS，2009：369-375.

[7]崔建国，李忠海，张大千，等.复杂性测度在肌电信号模式识别中的应用[J].计算机工程与应用，2006，42（11）：195-197.

[8]孙斌，周云龙，钟金山.基于复杂度特征的气液两相流流型识别方法[J].化学工程，2008，36（4）：27-30.

[9]张胜，乔世妮，王蔚.抑郁症患者脑电复杂度的小波熵分析[J].计算机工程与应用，2012，48（4）：143-145.

[10]Vapnik V.The nature of statistical learning theory[M].New York：Springer-Verlag，1995.

[11]Chen N Y，Lu W C，Yang J，et al.Support Vector Machine in chemistry[M].Singapore：World Scientific Publishing Company，2004：24-30.

[12]王凯，张永祥.遗传算法和支持向量机在机械故障中的应用[J].机械强度，2008，30（3）：349-353.

[13]崔建国，李一波，李忠海，等.基于小波包与支持向量机的复杂信号模式识别[J].数据采集和处理，2008，23（2）：163-168.

[14]朱学冬，胡平.基于最优二叉树的多故障分类器的设计[J].北京联合大学学报：自然科学版，2009，23（2）：26-29.

[15]李峰，汤宝华，章国稳.基于舍一交叉验证优化最小二乘支持向量机的故障诊断模型[J].振动与冲击，2010，29（9）：170-174.