一种基于凸包近似的快速体积计算方法

徐 志，许宏丽

XU Zhi,XU Hongli

北京交通大学 计算机与信息技术学院，北京 100044

School of Computer&Information Technology,Beijing Jiaotong University,Beijing 100044,China

近年来基于点的图形学（Point-based Graphic）研究受到了广泛的关注。人们对点的技术进行大量的工作，特别是在点云表示、点云造型、点云绘制等方面取得了许多新的进展[1]。然而，点云模型还很难应用到实际的应用系统中，原因就是点云模型的体积等积分属性很难计算。体积是点云模型重要的几何属性，在许多应用场景需要被频繁地计算。

物体的点云模型是在物体表面扫面点的集合。点的采样集合作为一种新的曲面表示方式，无需存储维护全局一致的几何拓扑信息，因而能够对复杂的3D模型进行高效的绘制和灵活的集合处理。快速计算点云模型的体积具有重要意义，如在使用激光雷达作为信息采集设备的塌方预警系统中，需要通过判别物体变化的体积与位移来确定灾害发生的等级；在模型自动识别系统中，通过计算多个点云模型的体积预先判别模型是否一致。

目前，就点云模型而言，体积的计算首先要重构点云曲面模型。近年来，曲面重建算法现在是计算机图形学领域的热门研究课题，经典算法有零集法、Poisson重建法[2]、Delaunay网格重建[3]及基于径向基函数的方法。Ohtake分别把多尺度CS-RBF与自适应CS-RBF应用到点云数据的三维建模中，其模型表面的质量更好，其抗噪能力也更强[4]。但是使用重建曲面来计算体积的方法，把工作集中在重构算法上，需要额外消耗大量的运算时间与空间，这样，对于只需要快速求取体积的应用系统中多出了许多工作。重建曲面可能会失败从而导致无法求取体积，以至于系统失效。

三维凸包在诸多应用中都发挥着重要作用，在计算机动画领域内，凸包被用来近似相撞物体加速碰撞检测，大大减少了检测所耗的时间[5]。本文把重点工作放在如何快速地求取物体体积上，这就需要折中物体的近似程度。一方面，希望它们尽可能简单，这样求体积的代价才会更低，而另一方面，新的物体近似的越是简单，所求的体积的误差也就越大。在各种方案中，有一个选择就是采用包围球的方式，而包围盒的体积代价很小，但是对于许多物体来说包围球的效果并不好。另外一个选择就是选择凸包，尽管与球体相比，凸包的计算更为复杂，但是大多数物体都可以通过凸包得到更好的近似。

1 凸包近似求体积

1.1 三维凸包的构建

从数学上看，在实向量空间中点集P凸包定义为包含P的最小凸集。在线性代数上，凸包定义为点集P的所有凸组合，公式表示为：

其中α，n为常系数。

在三维空间中，凸包可以定义为“集合内所有点凸组合所构成的集合”。通俗来讲，一组物品混合物的所有可能性构成了这组物品的凸包。

由欧拉公式可知，对于任意凸多胞体P，若体内包含n个顶点，则P中所含的边不会超过3n-6条，所含的小平面不会超过2n-4条。所谓的单纯多胞体即上述边及小平面达到最大的情况。因此，在三维空间中，任意n个点的凸包的复杂度为O(n)[6]。

在这里，将借助随机增量式算法来构造点集P的凸包。首先定义可见区域和地平线。假设 pr落在凸包ℓℏ(pr-1)之外，站在 pr点的位置，朝 ℓℏ(pr-1)看去，在 ℓℏ(pr-1)的表面上，那些可见的小平面连在一起组成了一个连通区域，把它称之为点 pr在凸包ℓℏ(pr-1)上的可见区域。而围成这个区域的ℓℏ(pr-1)上的边组成的折线，称之为点 pr在凸包ℓℏ(pr-1)上的地平线。具体算法描述如下：

算法 Incre_Convex（P）

输入：三维空间中的n个点组成的集合P

输出：P的凸包

（1）在P中选出不共面的四个点，构成一个四面体，作为初始凸包 ℓℏ(p4)。

（2）初始化凸包ℓℏ(p4)，确定各个面的方向，对凸包外的可见点成右手系方向。

（3）取其余各点的一个随机排列：p5，p6，p7，…，pn，循环逐一处理各点，并动态维护凸包。

（4）若 pr落在 ℓℏ(pr-1)的内部或边界，则有 ℓℏ(pr-1)=ℓℏ(pr)，转步骤（5）。

（5）若 pr落在 ℓℏ(pr-1)的外部，深度搜索遍历 ℓℏ(pr-1)，寻找点 pr在凸包ℓℏ(pr-1)上的地平线和所在平面。

（6）将 pr在凸包 ℓℏ(pr-1)上的可见区域内的所有面删除，并沿着地平线将 pr连接形成新的面，同时维护它的方向，将其加入凸包 ℓℏ(pr-1)，形成新的凸包 ℓℏ(pr)。

（7）重复步骤（4）～（6），直至处理完所有的点。

（8）结束

1.2 投影法计算体积

注意到上述所求三维凸包实际上是个三角网格模型，可以使用投影法[7]来计算三维凸包的体积。首先选择一个不与凸包任意三角面片相交的面作为投影面，为简化计算和便于理解，选择XOY平面作为投影面。如图1所示，将三维凸包ℓℏ(P)正投影在平面XOY上，得到投影面P，以该投影面的边界为准线，垂直于投影平面的直线为母线作棱柱，此棱柱侧面与凸包外壳的交面在投影平面上的正投影即是投影区域的边界，如图1所示。

图1 投影法

以上述正投影的方法，此棱柱侧面与凸包外壳的交面可以将凸包分为上三角网格面PU、下三角网格面PL和与棱柱侧面相重合的三角网格Pc。PU与PL与其在平面XOY下的投影组成两个凸多面体TU与TL，而三角网格Pc与平面XOY垂直，故所求凸包体积V(ℓℏ(P))=V(TU)-V(TL)，如图2，图3所示。

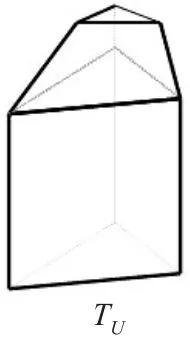
图2 上三角网格

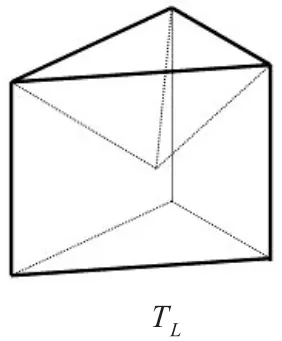
图3 下三角网格

已知上三角网格面与下三角网格面都有三角面片组成。以上三角网格面为例，对于每一个三角面片t与投影面XOY组成一个凸五面体，故有：

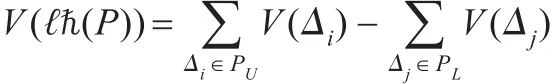
对于每一个凸五面体的体积V(Δi)可以分解为三个小四面体体积之和。由解析几何知，四面体积可以由边向量的混合积得到。以向量a，b，c为棱的四面体的体积可以表示为：(abc)=6εV ，当 a，b，c构成右手系时 ε=1，当 a，b，c构成左手系时ε=-1。

同时，也可以用这种方法来判断凸包的三角面片是属于上三角网格面还是下三角网格面。取三角面片的任一点在XOY面上的投影点与三角面片构成四面体，当ε=1时，该面片属上上三角网格面，当ε=-1时，该面片属于下三角网格面，当ε=0时，该三角面片与投影面XOY垂直。

构什么？几何图形是由点与线构成，对于线基于尺规可以构造直线与弧线.因为两点确定一条直线，所以构直线其实就是构造两点；因为弧线取决于圆心与半径，圆心与弧上任一点确定，其弧线也就确定，所以构造弧线也是构造两点.总而言之，可以明确构什么？就是构造点.

如图4所示，对于凸五面体ABCabc体积：

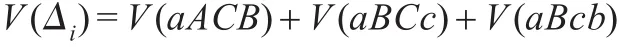
在这里要注意点的顺序要求。

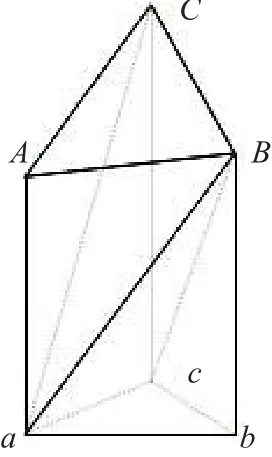
图4 凸五面体

至此就求出了整个三维凸包的体积，由此得出算法的基本描述。

算法 Vol_Convex3D（P）

输入：三维空间中的n个点的三维凸包

输出：三维凸包的体积

（2）遍历输入凸包的每一个三角面片 p1p2p3，分别求其在XOY面上的投影 pt1pt2pt3。

（3）按照右手法则，分解凸五面体 p1p2p3pt1pt2pt3，其固定顺序见式子。

（4）判断三角面片 p1p2p3是否在 pt1的可见区域内，若在，则所求体积符号为负，若不在，所求体积符号为正。

（5）求和，所有凸五面体体积的代数和即所求体积。

（6）结束。

2 实验结果

由于点云的原始体积数据很难获得，使用Image Ware产生若干点云数据并预先手动计算其真实体积，用其测试算法准确度。再取若干组实际点云模型，测试算法效率。实验结果如图5、表1所示。

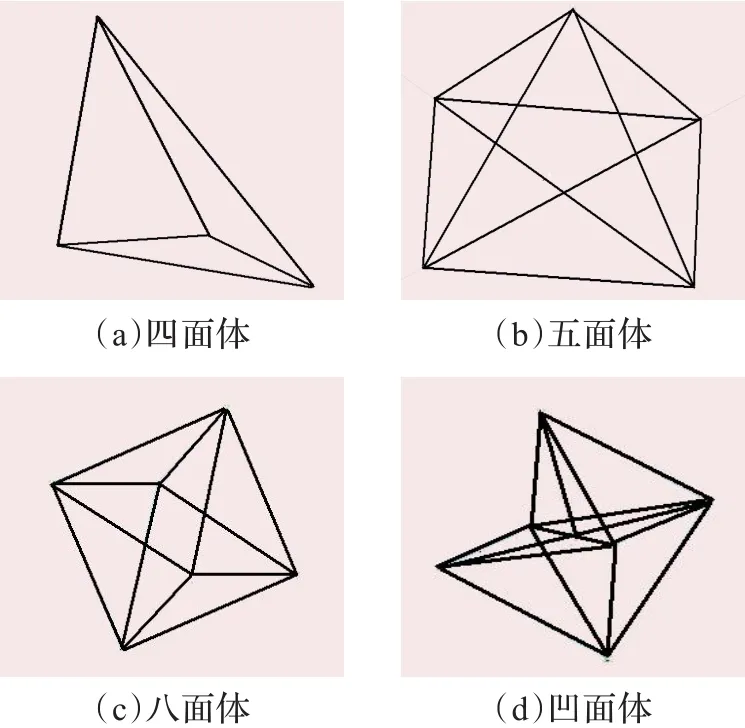
图5 测试点云模型

表1 测试数据体积、正确率表

实验结果表明，算法在计算凸形点云模型上准确率高，而对于非凸物体存在一定误差。在实验环境Pentium D 2.8 GHz，DEV C++环境下使用实际点云数据模型结果如图6、表2所示。

图6 实际点云模型

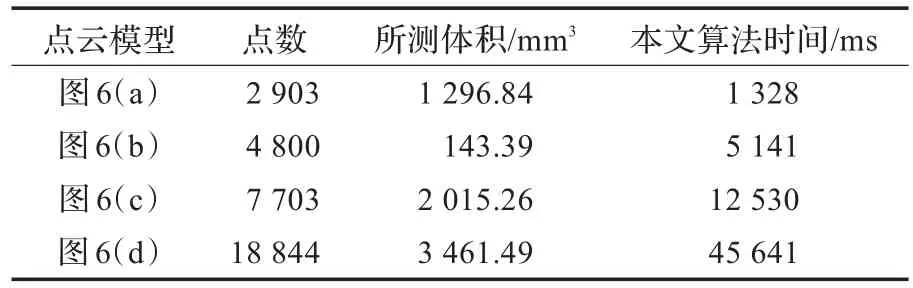
表2 测试数据体积、算法时间表

由于算法减少了完全重构三维模型的过程，简化了后一步求取体积的过程，其后续求体积的时间复杂度为O(n)，因此算法主要依赖于凸包算法的复杂度，减少了很多不必要的时间消耗，实验表明，算法可快速有效地求解处理具有复杂拓扑结构的点云模型，杜绝了传统曲面算法重构求解失败的可能。

3 结束语

本文针对要求实时性可靠性较高的点云模型体积计算系统，设计了一种快速凸包近似计算方法，实现了一种无须进行点云模型重建曲面直接求取点云体积的算法，避免了重构时消耗的大量时间，也杜绝了对于有较为复杂的拓扑结构的点云模型，重建曲面可能会失败从而导致无法求取体积的情况。最后进行了实验，实验表明本算法能快速地求出点云模型的体积，对于凸形模型准确率高，而非凸的模型存在一定误差，其准确率还有待提高，其更适合于计算对象是凸的或者对要求精度不高但实时性要求高的系统。

另外，算法的效率还有待提高，对于某些系统上存在大量的点云数据，考虑采用建立内外包围盒的方法先对数据点进行精简[8]并对三维凸包算法的时间复杂度进行优化研究，进一步提高算法的准确率和效率。

[1]Gross M，Pfister H.Point-based graphics[M].[S.l.]：Morgan Kaufmann Publisher，2007：1-3.

[2]Kazhdan M，Bolitho M，Hoppe H.Poisson surface reconstruction[C]//Polthier K，Sheffer A.Symposium on Geometry Processing.Switzerland：The Eurographics Association，2006：61-70.[3]Dey T，Giesen，Hudson.Delaunay based shape reconstruction from large data[C]//Parallel and Large-Data Visualization and Graphics Proceedings，2001.

[4]Ohtake Y，Belyaev A，Seidel H P.A multi-scale approach to 3D scattered data interpolation with compactly supported basis functions[C]//Proceedings of Shape Modeling International，2003：153-161.

[5]Berg M D，Kreveld M V，Overmars M，et al.Computational geometry：algorithms and applications[M].邓俊辉，译.[S.l.]：Springer-Verlag，2005.

[6]Barber C B，Dobkin D P.The quickhull algorithm for convex hulls[J].ACM Transactions on Mathematical Software，1996，22.

[7]王泉德.任意三角网格模型体积的快速精确计算方法[J].计算机工程与应用，2009，45（18）：32-34.

[8]孙殿柱，朱昌志，李延瑞.三维散乱点云凸包快速求解算法[J].机械设计与研究，2009，25（4）：11-14.