蚁群算法参数组合的博弈优化

郜庆市，孙树栋，韩 青，钟 尧

GAO Qingshi,SUN Shudong,HAN Qing,ZHONGYao

西北工业大学 机电学院，西安 710072

School of Mechanical Engineering,Northwestern Polytechnical University,Xi’an 710072,China

1 引言

蚁群优化算法（Ant Colony Optimization，ACO）[1]是一种基于自然界中蚂蚁种群觅食行为的新型优化算法。最早是由Dorigo及其研究团队提出，用来解决旅行商（Traveling Salesman Problem，TSP）等一系列的组合优化问题。算法具有正反馈、分布式计算与启发式函数相结合的优点[2]，更易于发现更优的解，并且易于与其他方法结合，具有较强的鲁棒性，使得该算法逐渐引起许多研究者的注意，并将其应用于很多具体的实际问题中[3]。

在ACO算法中，信息素、启发式函数和蚂蚁之间的合作直接影响算法的收敛性，而信息式启发因子α、期望启发因子 β、信息素挥发因子ρ、信息素增强系数Q、蚁群数目K等参数的选择对算法的收敛性起到关键性作用，恰当选取参数组合可使得ACO算法更易于得到“利用-探索”平衡关系，收敛到最优。然而，到目前为止仍没有一种行之有效的数学分析方法来确定ACO算法的参数组合。现在普遍采用的方法是基于大量的实验，靠经验和直觉选择参数组合。本文提出了一种基于博弈论的ACO参数组合优化模型，该模型利用数学分析方法，理论上优化出不同环境下的参数组合，使ACO算法能够在相对较短时间下收敛到最优。

2 蚁群算法简介

蚁群优化算法的过程主要包括选择、更新和调整三个过程。假设蚁群数目为 K，dij(i=1，2，…，n1;j=1，2，…，n2)为节点i与 j之间的距离，τij(t)表示t时刻在路径(i，j)上的信息素。任意一蚂蚁k在运动过程中，根据下式的概率转移规则转移方向：

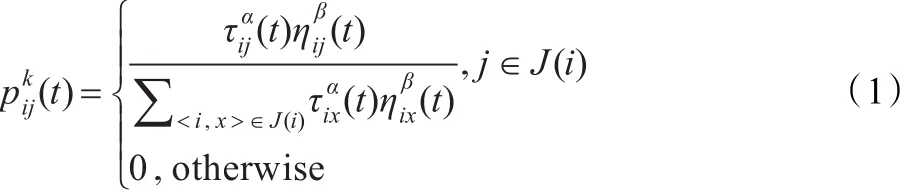
式中，ηij(t)为启发式函数，一般取 ηij=1/dij；参数 α和 β分别为信息素和启发式函数对整个转移概率的影响权值；J(i)表示蚂蚁k在节点i处的可行邻域。

随着时间的推移，信息素会逐渐挥发，用参数(1-ρ)表示信息素挥发后的剩余度，当一个循环周期结束后，进入t+1时刻，此时各路径上的信息素将按照下式更新：

3 蚁群收敛速度分析

本章将从数学角度给出蚁群收敛速度的分析，为博弈论优化蚁群参数组合模型提供有效的收益函数。

定义1 γ为ACO算法的收敛时间，Eγ为算法的期望收敛时间。

期望收敛时间表示的是当ACO算法的迭代时间t大于等于Eγ时，ACO算法以概率为1绝对收敛并且达到全局最优解的时间。Eγ越大表明算法的收敛速度越慢，效率越低；反之，说明算法的收敛速度越快，效率越高。

定义2σ为ACO算法首次达到全局最优解的收敛时间，Eσ为首次达到全局最优解收敛时间的期望。

定理1 ACO算法的收敛时间γ等于首次达到最优解的收敛时间σ。

证明 文献[4-5]中已经证明ACO算法具有Markov性。令ψ(t)表示在第t次迭代的状态参数即信息素集与路径解集，ψ*表示全局最优解下ACO算法的状态参数。根据Markov性质可知：当 t=σ 时，P(ψ(σ+1)∉ ψ*|ψ(σ)∈ ψ*)=0 ；P(ψ(σ)∈ψ*)=1时，P(ψ(σ+1)∈ψ*)=1；因此可知当且仅当 t大于σ时，ACO算法以概率为1绝对收敛，则根据定义1有σ=γ。

因此，可以只通过计算Eσ来得到蚁群的期望收敛时间，下文计算的Eγ实际均为Eσ。

定理2 ACO算法的信息素满足：

证明 根据式（2）和文献[6]可知路径(i，j)上信息素的最小值为蚂蚁在迭代时间t之前没有探索过该路径，信息

根据式（2）和式（3）可知：

利用数学归纳法可得信息素的上界：

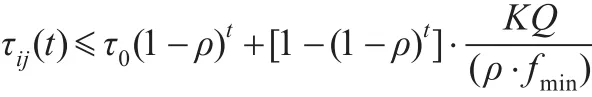
根据文献[4]提到可知：

其中n为最优路径解集中节点的个数；K为蚁群数目；plow为在最优解集ψ*上概率选择的理论最小值。

定理3 ACO的期望收敛时间Eγ满足：

其中ηimax为蚂蚁在节点i时选择下一可行节点中启发函数中的最大值。

证明 根据式（1）可知：

将上式代入到式（5）即可得到定理3结论成立。

4 基于博弈论的ACO算法参数优化设计

4.1 博弈论三要素

博弈论又名对策论，主要研究的是策略相互依赖行为。局中人相互之间有利益冲突，决策行为相互影响，局中人采取理性决策以最大化自身利益。

无论何种博弈论模型，总是包括以下三个要素[7]：

（1）局中人集合 N={1，2，…，n}。

（2）每个局中人i有若干个策略可供选择，它构成该局中人的纯策略空间 Si={λi1，λi2，…，λiki}。定义在 Si的一个概合策略集，其中xim表示选择纯策略λim的概率，其中：

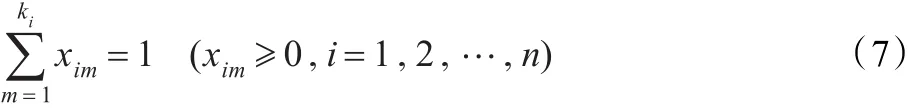
（3）若每个局中人选定一个策略 λi∈Si，就形成了一个局势 s={λ1，λ2，…，λn}，每个局中人 i都有自己相应的收益函数，对于局中人i在局势s下的收益函数为 Pi(s)=Pi(λ1，λ2，…，λn)。

n人博弈对策可用 Γ=(N，{Si}，{Pi})表示，设 x为对策 Γ的一个混合局势，记 x||Xi=(x1，…，xi-1，Xi，xi+1，…，xn)，其Xi，其他局中人的混合策略不变，产生的新的混合局势。

定义3假设x*为对策Γ的一个混合局势，如果

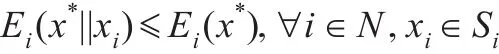
其中：

则称 x*为n人对策Γ的一个混合平衡局势即Nash平衡点[8]。

4.2 参数组合优化设计

对于ACO算法参数的组合优化，由于各个参数之间相互依赖、相互影响，单独地研究某一参数对算法的影响很难得出较优的参数组合，本节从4.1节博弈论三要素出发，构建ACO算法参数的博弈优化模型，并证明其可行性。

（1）将ACO的关键参数视为博弈论模型中的局中人，参数集合 L={α，β，K，ρ}。

（2）根据文献[9-10]验证的结论可知：ACO算法各参数都有相对应的取值范围即纯策略集。由于博弈论研究的策略空间为离散的，首先需要将各参数的纯策略集离散化处理：

其中，λi表示参数可选的第i个策略值；li表示参数取值范围的左极限；ui表示参数取值范围的右极限；mi表示参数策略集中策略的个数。

利用式（8）得到ACO算法的参数纯策略集分别为Sρ，SK，Sα，Sβ即

其相对应的混合策略集分别为：

利用式（8）选取参数的纯策略空间时，选取的策略空间越大，优化后的参数组合越准确，但相应会增加模型的运算时间，因此参数空间不易选择太大。

（3）根据定理3给出的ACO算法收敛速度不等式（6）令

选取ACO各参数的收益函数为：

定理4博弈论模型规划出的ACO算法的最优参数组合与实际ACO算法的最佳参数组合理论上具有一致性。

证明 根据定理3中蚁群收敛时间与各个参数关系的不等式可知：理论上求ACO参数最优组合问题可转化为求函数g的最小值问题即在函数g达到最小值的情况下对应的参数组合即为最优的参数组合。

根据最值定理可知：若函数对未知数偏导数值等于零的点存在，则该零点对应的为函数的最值点；若偏导数等于零的点不存在，根据偏导数实质为未知数对于函数的变化率（梯度），可知未知数对函数变化率的最小的点即逼近零点的点为理论上的最优点。

因此利用博弈论模型求ACO算法参数组合的最优解参数组合只需要求得函数g最小值点对应的未知数的值，也就是理论上实际蚁群参数的最优组合即

其中，i表示ACO算法的参数。

由定义3可知，博弈论中的Nash均衡点策略组合实质为所有局中人最优策略的组合，即局中人的收益函数最大值点。

令ACO算法博弈优化参数组合模型中收益函数最大值点表示为：Pimax(s*)。

根据式（9）与式（10）可知基于博弈论优化ACO算法参数组合模型求解出的参数最优组合与实际的参数最优组况下的参数最优组合解，因此可知两者理论上具有一致性。

5 模型仿真与分析

为了验证本文提出的参数优化组合模型的有效性，本文采用TSPLIB[11]中的Oliver30、Eil51问题作为标准化问题，使用Matlab7.11.0环境下进行算法模型的仿真验证。分别采用本文构建的博弈模型求解出的最优参数组合与文献中给出的参数组合运行经典的TSPLIB问题，比较不同参数下ACO算法的性能。根据文献[9-12]中描述，本文选取参数的取值范围如表1所示。

表1 蚁群算法参数取值范围

为了验证不同参数ACO算法的收敛时间，本文采用的最大循环次数为800次，初始信息素τ0=5，信息素增强系数Q=78。

5.1 OLIVER30

针对Oliver30问题，文献[10]和文献[12]中都给出了一组优化参数，基于本文模型同样得到了一组优化参数如表2。

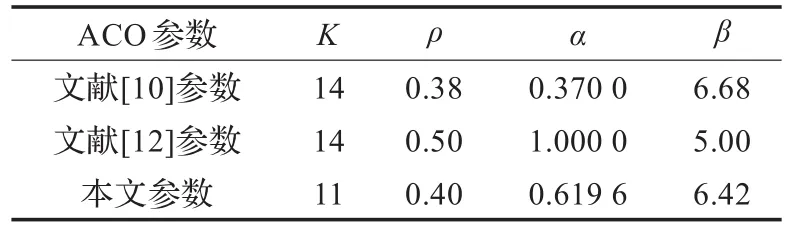
表2 文献与仿真得到的参数组合

图1为分别采用表2的参数组合进行了200次实验的ACO算法的收敛时间与最短路径的曲线图。（a）为文献[10]所提出的参数组合的仿真曲线图，（b）为文献[12]的仿真曲线图，（c）为本文模型得到的参数仿真曲线图。根据图1可以得到实验结果数据分析表3。

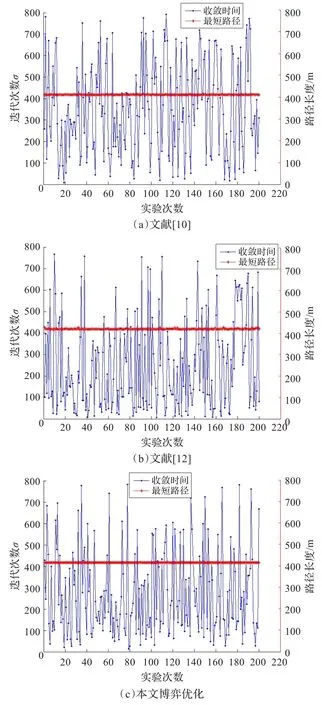
图1 Oliver30收敛时间与最短路径曲线

由表3可以看出图1（c）仿真的实验结果明显优于图1（a）、图1（b），即利用博弈论模型得出的参数组合可使ACO算法在寻找最优路径时有很好的稳定性（标准偏差较小），Antcycles（Ant-cycles为实验的蚂蚁种群K与平均收敛时间的乘积）较小，蚁群算法运行时间较短。

表3 Oliver30实验数据结果

5.2 EIL51

本节对Eil51问题进行进一步的仿真验证，利用文献[10]与博弈模型给出的ACO参数组合来验证模型的有效性，表4对应参数组合。

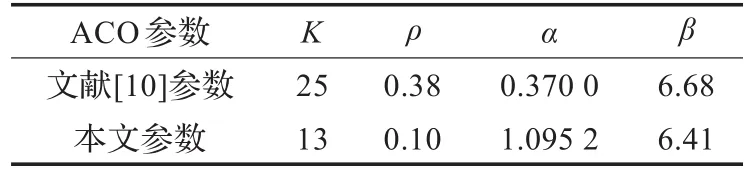
表4 文献与仿真得到的参数组合

图2中（a）为文献[10]中参数的实验仿真曲线图，（b）为本文模型得到的参数仿真曲线图。

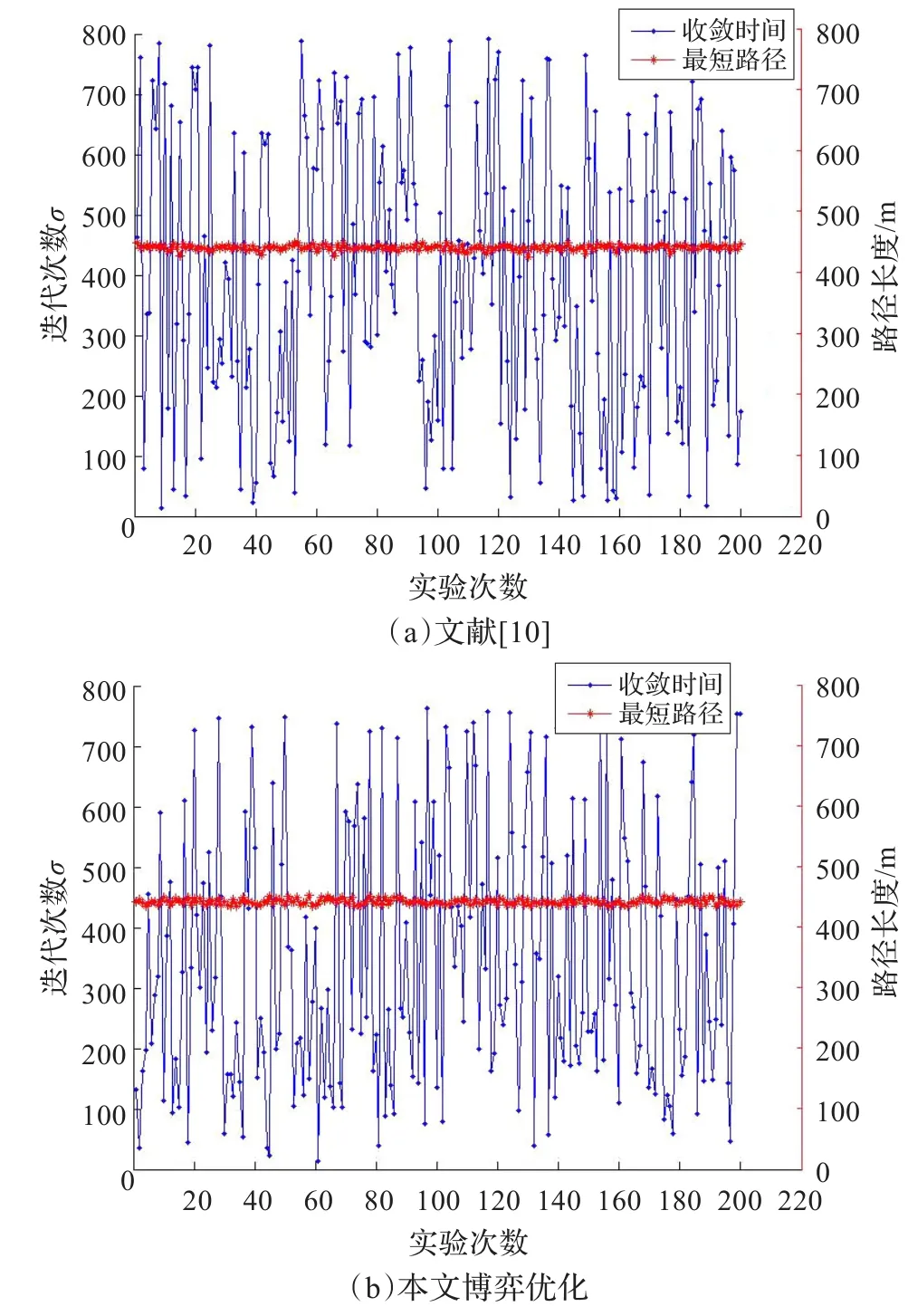
图2 Eil51收敛时间与最短路径曲线

根据图2得到的数据结果表5同样可以看出基于博弈论的ACO算法参数组合模型得出的参数组合在极大提高算法收敛时间的同时仍具有较好的稳定性，进一步说明模型的正确性和有效性。

表5 Eil51实验数据结果

6 结束语

本文将博弈论模型与蚁群算法结合，提出了一种基于博弈论对ACO算法的参数进行组合优化的模型。本文利用算法参数的相互依赖、相互影响的特性，将参数看做博弈论中的局中人进行参数组合优化。仿真实验结果证明了该模型的有效性，并且针对不同的环境，该模型可以规划出相应的较优参数组合，更加有利于ACO算法的应用。

[1]Dorigo M，Maria L.Ant colony system：a cooperative learning approach to the traveling salesman problem[J].IEEE Trans on Evolutionary Computation，1997，1（1）：53-66.

[2]李士勇.蚁群算法及其应用[M].哈尔滨：哈尔滨工业大学出版社，2004.

[3]段海滨，王道波，朱家强，等.蚁群算法理论及应用研究的进展[J].控制与决策，2004，19（12）：1321-1326.

[4]Huang Han，Wu Chunguo，Hao Zhifeng.A pheromone rate-based analysis on the convergence time of ACO algorithm[J].IEEE Trans on Systems，2009，39（4）：910-923.

[5]Duan Haibin，Wang Daobo，Yu Xiufen.Markov chains and martingale theory based convergence proof of ant colony algorithm and its simulation platform[C]//Proceedings of the 6th World Congress on Intelligent Control and Automation，Dalian，China，2006.

[6]朱庆保.蚁群优化算法的收敛性分析[J].控制与决策，2006，21（7）：763-766.

[7]沈士根，马绚，蒋华，等.基于演化博弈论的WSNs信任决策模型与动力学分析[J].控制与决策，2012，27（8）：1133-1138.

[8]谢政.对策论[M].长沙：国防科技大学出版社，2004.

[9]詹士昌，徐婕，吴俊.蚁群算法中有关算法的最优选择[J].科技通报，2003，19（5）：381-386.

[10]Botee H M，Bonabeau E.Evolving ant colony optimization[J].Adv Complex Systems，1998，1：149-159.

[11]孙凯，吴红星，王浩，等.蚁群与粒子群混合算法求解TSP问题[J].计算机工程与应用，2012，48（34）：60-63.

[12]蒋玲艳，张军，钟树鸿.蚁群算法的参数分析[J].计算机工程与应用，2007，43（20）：31-36.

[13]Dorigo M，Maniezzo V，Colorni A.Ant system：optimization by a colony of cooperating agents[J].IEEE Trans on Systems，Man and Cybernetics，1996，26（1）：29-41.