离散捕食系统的持久性和全局稳定性
王 烈,陈斯养
WANG Lie,CHEN Siyang
陕西师范大学 数学与信息科学学院,西安 710062
College of Mathematic and Information Science,Shaanxi Normal University,Xi’an 710062,China
1 引言
近年来,许多学者对差分模型的动力学性质进行了广泛的研究,获得了非常丰富的成果。文献[1-6]对自治差分模型的动力学性质进行了研究;文献[7-8]研究非自治的差分竞争模型的持久性和稳定性;文献[9-12]研究了非自治的差分捕食模型,获得了模型稳定性和持久性的条件。陈凤德等[11]研究了如下非自治的离散捕食模型:

其中 i=1,2,…,n,j=1,2,…,m 。
最近的研究表明,Beddington-DeAngelis功能性反应函数可以更好地刻画多个食饵和捕食者的种群密度增长情况,因此文献[13-16]讨论了该功能性反应函数在一些食饵-捕食者模型中的应用。
基于以上研究,本文研究如下具有Beddington-DeAngelis功能性反应和时滞的离散捕食系统:

其中 i=1,2,…,n,j=1,2,…,m 。 xi(k)是第 i个食饵种群的种群密度,yj(k)是第 j个捕食者种群的种群密度。参数 bi(k),hil(k),ail(k),cij(k),αij(k),βij(k),γij(k),dij(k),ejl(k),gjl(k)和rj(k)均为有界非负数列。参数 τil,τ*jl是正整数。
考虑到系统生物学意义,系统式(2)满足如下的初始条件:

其中 k∈{-τ,-τ+1,…,0},ϕi(k)和 ψj(k)均为实值有界数列,τ=max{。
为讨论方便,对任一有界数列{x(k)},引入如下记号:

2 系统式(2)的持久性
如果存在两个正数m和M ,使得系统式(2)的任一正解 (x1(k),x2(k),…,xn(k), y1(k),y2(k),…,ym(k))满足:

其中i=1,2,…,n,j=1,2,…,m,则称系统式(2)是持久的。
命题2.1系统式(2)的任一正解满足:

证明 首先假设存在一个k0,使得 xi(k0+1)≥xi(k0)成立。则从系统式(2)的第i个等式可知:

其中,A0=αil(k0)+βil(k0)xi(k0)+γil(k0)yl(k0)。
对式(5)进行移项放缩,可得:

当x>0时,不等式 x≤exp(x-1)恒成立,从而可得0<≤exp(-1);如果参数a,b>0,则有如下结论:
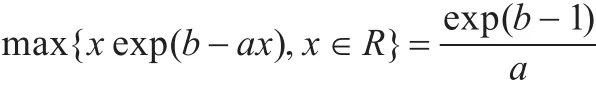
由以上两个结论和式(6)可得:

如下使用反证法证明当k0≤k<+∞时,xi(k)≤Si成立。假设存在最小的正整数 k͂0> k0,满足 xi(k͂0)> Si,则可知 k͂0≥k0+2 且 xi(k͂0-1)≤ Si< xi(k͂0)。由式(7)和 xi(k͂0-1)≤Si可知 xi(k͂0)≤Si,与假设矛盾。因此当 k0≤k<+∞ 时,xi(k)≤Si成立。
其次假设 xi(k)>xi(k+1)对所有 k∈N都成立,且记系统式(2)的第i个等式取极限,可知:
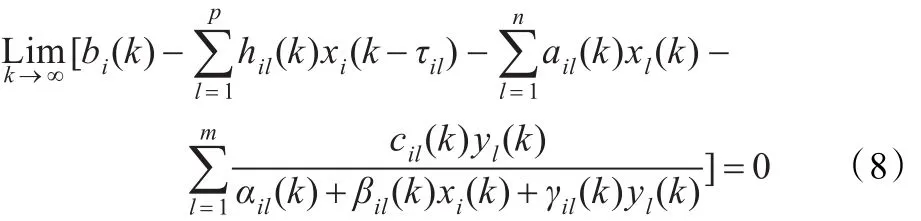
但是,当k足够大时,可知:

综合如上的讨论可知,命题2.1成立。
利用命题2.1的证明思想、方法,可给出如下命题2.2~命题2.4,并将其证明过程略去。
命题2.2假设如下条件成立:

则系统式(2)的任一正解满足:

设

其中 i=1,2,…,n。
命题2.3假设条件(H1)和以下条件:

成立。则系统式(2)的任一正解满足:

设

其中 j=1,2,…,m。
命题2.4 假设条件(H1)、(H2)和以下条件:

成立。则对系统式(2)的任一正解满足:

应用命题2.1~命题2.4,可得系统式(2)持久的结论:
定理2.1 假设条件(H1)~(H3)成立,则系统式(2)是持久的。
显然,集合:

是系统式(2)的不变集。
3 系统式(2)的全局稳定性
在本章中使用估值法对系统式(2)的稳定性进行讨论。
令
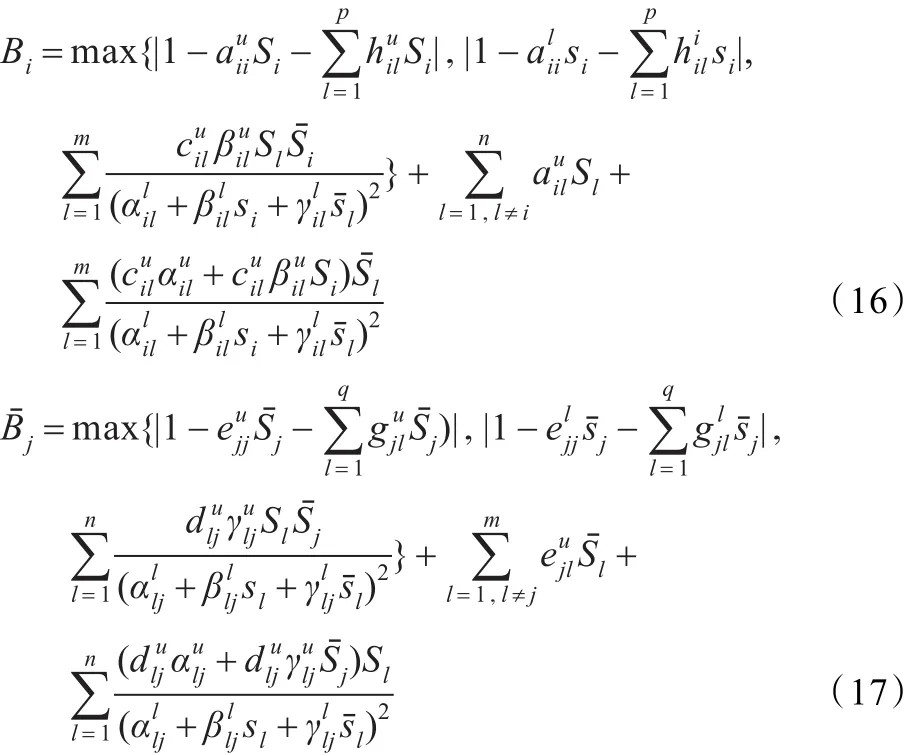
其中i=1,2,…,n,j=1,2,…,m。
定理3.1假设条件(H1)~(H3)成立。如果如下条件满足:

则系统式(2)的任意两个解满足:

其中i=1,2,…,m,j=1,2,…,n。
证明设

将其代入系统式(2),可得:
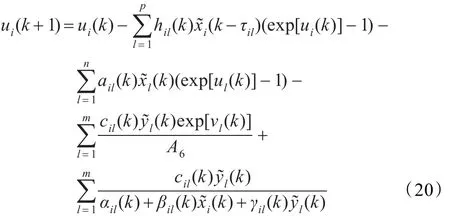
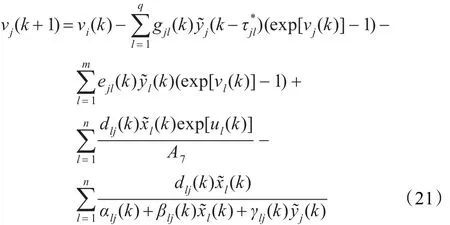
其中

对式(20)和式(21)进行化简,可得:

对任意足够小的 ε>0,结合(H4)和(H5),可得:

其中

其中

根据命题2.1~命题2.4,可知存在一个k*∈N,对所有k≥k*满足:其中 i=1,2,…,n, j=1,2,…,m 。

由于 θl(k),ξl(k)∈[0,1],从而可知 x͂i(k)exp[θi(k)ui(k)]位于 x͂i(k)和 xi(k)之间,y͂j(k)exp[ξj(k)vj(k)]位于 y͂j(k)和 yj(k)之间。
由式(22)~(26),可知:

式(27)和式(28)可知,当 k≥k*时,

从而可得:
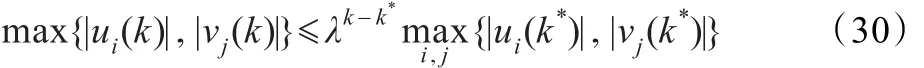
即

4 周期解的存在性和稳定性
在本章中,进一步讨论当系统式(2)中的参数出现周期的情况。引入如下假设:
(H6)bi(k),hil(k),ail(k),cij(k),αij(k),βij(k),γij(k),dij(k),ejl(k),gjl(k)和rj(k)是周期为ω>0的正有界数列。
定理4.1 假设条件(H1)~(H3)和(H6)成立,则系统式(2)至少存在一个具有周期为ω>0的正周期解(x͂1(k),x͂2(k), …, x͂n(k), y͂1(k), y͂2(k), …, y͂m(k))。
证明 在不变集Dn+m上定义映射F,其表达式为:

由于映射F是连续的,而且是定义在紧集Dn+m上一个自身到自身的映射,由不动点原理可知,映射F具有一个不动点,即系统式(2)在集合Dn+m上至少存在一个具有周期为ω的正周期解。
根据命题2.1~命题2.4和定理4.1,可得如下结论:
定理4.2 假设条件(H1)~(H3)和(H6)成立,则系统式(2)存在一个周期为ω>0的正周期解,而且该周期解是全局稳定的。
5 结论
本文对一类带有Beddington-DeAngelis功能性反应和时滞的多维离散食饵-捕食系统进行了研究。首先利用差分方程的比较原理,对模型的任一正解的上下界进行了估值,得到模型持久性的充分条件。其次应用估值方法推导得到系统全局稳定性的充分条件。最后,讨论了模型参数出现周期的情况,使用不动点理论证明了系统周期解的存在性和全局稳定性。研究结果表明Beddington-DeAngelis功能性反应对模型的持久性和全局稳定性的充分条件有着重要的影响,但还需进一步讨论时滞对模型动力学行为的影响。
[1]Cull P.Global stability of population models[J].Bulletin of Mathematical Biology,1981,43(1):47-58.
[2]Cull P.Stability of discrete one-dimensional population models[J].Bulletin of Mathematical Biology,1988,50(1):67-75.
[3]Franke J E,Yakubu A A.Mutual exclusion versus coexistence for discrete competitive systems[J].Bulletin of Mathematical Biology,1991,30(1):161-168.
[4]Franke J E,Yakubu A A.Geometry of exclusion principles in discrete systems[J].Journal of Mathematical Analysis and Applications,1992,168(2):385-400.
[5]Kocic V K,Ladas G.Global behavior of nonlinear difference equations of higher order with applications[M].Dordrecht,Netherland:Kluwer Academic Publishers,1993.
[6]Saito Y,Ma W,Hara T.A necessary and sufficient condition for permanence of a Lotka-Volterra discrete system with delays[J].Journal of Mathematical Analysis and Applications,2001,256(1):162-174.
[7]Chen Y M,Zhou Z.Stable periodic solution of a discrete periodic Lotka-Volterra competition system[J].Journal of Mathematical Analysis and Applications,2003,277(1):358-366.
[8]Huo H F,Li W T.Permanence and global stability for nonautonomous discrete model of plankton allelopathy[J].Appl Math Lett,2004,17(9):1007-1013.
[9]Yang X T.Uniform persistence and periodic solutions for a discrete predator-prey system with delays[J].Journal of Mathematical Analysis and Applications,2006,316(1):161-177.
[10]Fan Y H,Li W T.Permanence for a delayed discrete ratiodependent predate or-prey system with holling type functional response[J].Journal of Mathematical Analysis and Applications,2004,299(2):357-374.
[11]Wu Liping,Chen Fengde,Li Zhong.Permanence and global attractivity of a discrete Schoener’s competition model with delays[J].Mathematical and Computer Modelling,2009,49(8):1607-1617.
[12]Chen Fengde.Permanence and global attractivity of a discrete multispecies Lotka-Volterra competition predator-prey systems[J].Applied Mathematics and Computation,2006,182(1):3-12.
[13]Naji R K,Balasim A T.Dynamical behavior of a three species food chain model with Beddington-DeAngelis functional response[J].Chaos,Solitons&Fractals,2007,32(5):1853-1866.
[14]Huo H F,Li W T,Nieto J J.Periodic solutions of delayed predator-prey model with the Benddington-DeAngelis functional response[J].Chaos,Solitons&Fractals,2007,32(2):505-512.
[15]Cantrell R S,Cosner C.On the dynamics of predator-prey models with the Beddington-DeAngelis functional response[J].J Math Anal Appl,2001,257.
[16]Cai Liming,Li Xuezhi,Yu Jingyuan,et al.Dynamics of a nonautonomous predator-prey dispersion-delay system with Beddington-DeAngelis functional response[J].Chaos,Solitons&Fractals,2009,40(4):2064-2075.

