融合DWT与2DLDA的人耳识别

屈智成，阳梦怡，魏玲江

（四川农业大学 旅游学院，四川 都江堰 611830）

近年来，人耳图像识别技术作为生物特征识别领域的新分支，越来越受到人们的关注.线性鉴别分析（LDA）是广泛应用的一种模式识别方法，也可应用于人耳特征的提取［1－2］.但 是LDA应用于人耳图像时，需要把二维图像矩阵转换为一维向量再进行投影，常常会导致图像中结构信息的丢失，而二维线性鉴别分析（2DLDA）直接将二维图像矩阵投影解决了该问题［3］.离散小波变换（DWT）广泛应用于数字图像分析，文中提出了将DWT 与2DLDA 相结合的人耳图像识别方法，该方法对人耳图像进行二维DWT 分解，选择其中的低频子带，在低频子带中利用2DLDA 提取人耳图像特征，最后使用最近邻法则进行分类实验.实验结果表明，该方法识别效果优于2DLDA方法.

1 离散小波变换

小波变换是现代谱分析工具，应用于信号处理、图像分析及编码、语音合成等许多科学领域，它是对傅里叶变换的一个重大突破，是傅里叶分析之后的又一有效的时频分析方法.与Fourier变换相比，它是一个时间和频域的局域变换，因而能有效地从信号中提取信息，解决了Fourier变换不能解决的许多困难问题.小波变换是先将母小波ψ（x）∈L2（R）经过伸缩和平移后得到小波基［4］

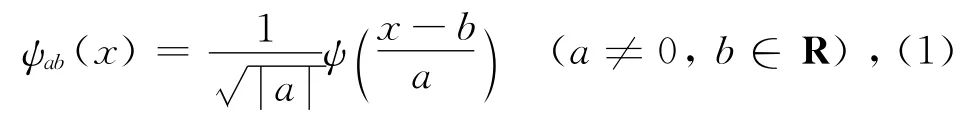
其中，a为伸缩因子，b为平移因子.

对于任意函数f（x）∈L2（R）的连续小波变换为［4］

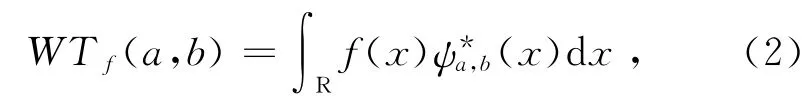
其中，ψ＊（·）是ψ（·）的复共轭.WTf（a，b）是a和b的函数，小波逆变换为［4］

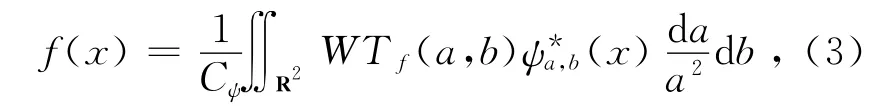
在上面的信号f（x）的连续小波变换定义中，a、b和x都是连续变量.小波变换实际利用计算机实现，需要将连续小波变换离散化，即将伸缩因子a和平移因子b进行离散化，通常进行二进制离散.现代图像多利用计算机处理，为了适应计算机对数字图像的处理，需要将一维小波变换推广到二维.图1为二维离散小波分解示意图，其中（a）图为对图像进行一层小波分解后获得四个不同频率的子带图.LL1子带代表图像的低频信息，保留了原图像的大部分特征，是原图像的近似子图像；HL1代表图像垂直方向的高频信息；LH1代表图像水平方向的高频信息；HH1代表图像对角方向的高频信息.（b）图是二层离散小波分解的示意图，其中的LL2、HL2、LH2、HH2是图（a）中的低频子带LL1经进一步小波分解得到的，LL2 为二层离散小波分解的低频分量.

图1 二维离散小波分解示意图Fig.1 The two－dimensional discrete wavelet decomposition schematic diagram

Haar小波是小波分析中常用的小波函数，图2为用Haar小波作为基函数时对人耳图像进行的离散小波分解的实例图示.图2（a）为原始人耳灰度图像；图2（b）为图像进行一层离散小波分解的图像；图2（c）为图2（b）中的左上角的低频子带图像，即一层离散小波分解的低频分量；图2（d）为原始图像二层离散小波分解得低频子带图.图像经小波分解后高频分量取值较小，大部分数值趋于0，而低频分量取值较大，集中了图像的大部分能量.

图2 基于Haar小波对人耳图像进行的离散小波分解图Fig.2 The discrete wavelet decomposition ematic diagram of human ear image based on Haar

2 二维线性鉴别分析

用LDA 进行二维图像特征提取时，常存在类内散布矩阵奇异而无法直接求得最佳投影的问题，而2DLDA 将二维图像矩阵直接投影解决了该问题［3］.

设训练样本集是由N个m×n维的图像｛x1，x2，…，xN｝组 成，且 分 别 属 于C类｛X1，X2，…，XN｝.如果第i类的样本数为Ni，那么样本总数为：

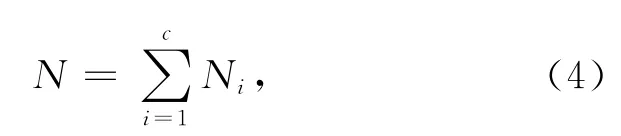
第i类样本类内均值和总样本均值μi、μ分别为：

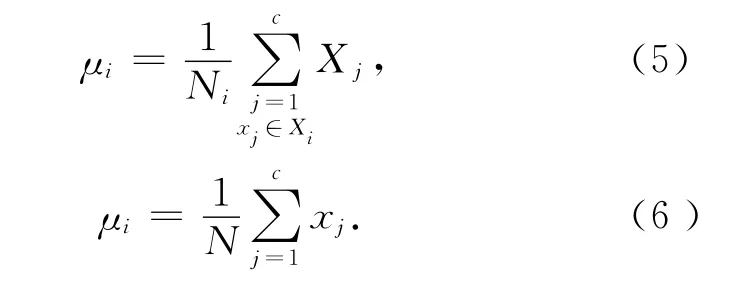
样本类内散布矩阵及类间散布矩阵Sw、Sb分别为［5－6］：

Fisher准则函数定义为：

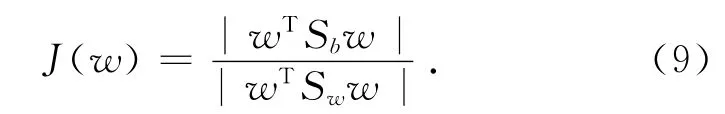
3 仿真实验

3.1 实验过程

本文采用了北京科技大学人耳识别实验室建立的人耳图像库1作为人耳识别实验的图像库［9］，该图像库有60人的180张人耳图像，每个人有3张人耳图像，3张图片分别为正面人耳图像、角度微变化人耳图像、光照微变化人耳图像，每张人耳图像大小为150×80pixel.实验采用每个人的正面人耳图片和角度变化图片作为训练样本；每个人的光照变化图片作为测试样本，实验步骤如下：

1）将训练样本和测试样本人耳图像利用haar小波进行一层离散小波分解，提取小波分解得到的低频子带系数.

3）计算测试样本人耳特征向量和训练样本人耳特征向量之间的欧氏距离，利用最近邻法则进行人耳图像特征分类.

将训练样本和测试样本人耳图像利用haar小波进行二层离散小波分解，提取二层小波分解得到的低频子带系数，重复2）和3）.

3.2 实验结果

实验程序在matlab2008a 软件上编写，在Pentium（R）4，3.06G CPU，1G 内存的计算机上运行.训练样本和测试样本先进行离散小波分解取低频子带系数，再进行二维线性鉴别分析（2DLDA），表1给出了采用一层小波和二层小波分解再进行2DLDA 与人耳图像直接进行2DLDA方法的正确识别率实验数据，其中k是选取最大特征值的个数.当特征值k取1，2，3，……，16时，本文方法与2DLDA 方法的正确识别率对照如图3所示.

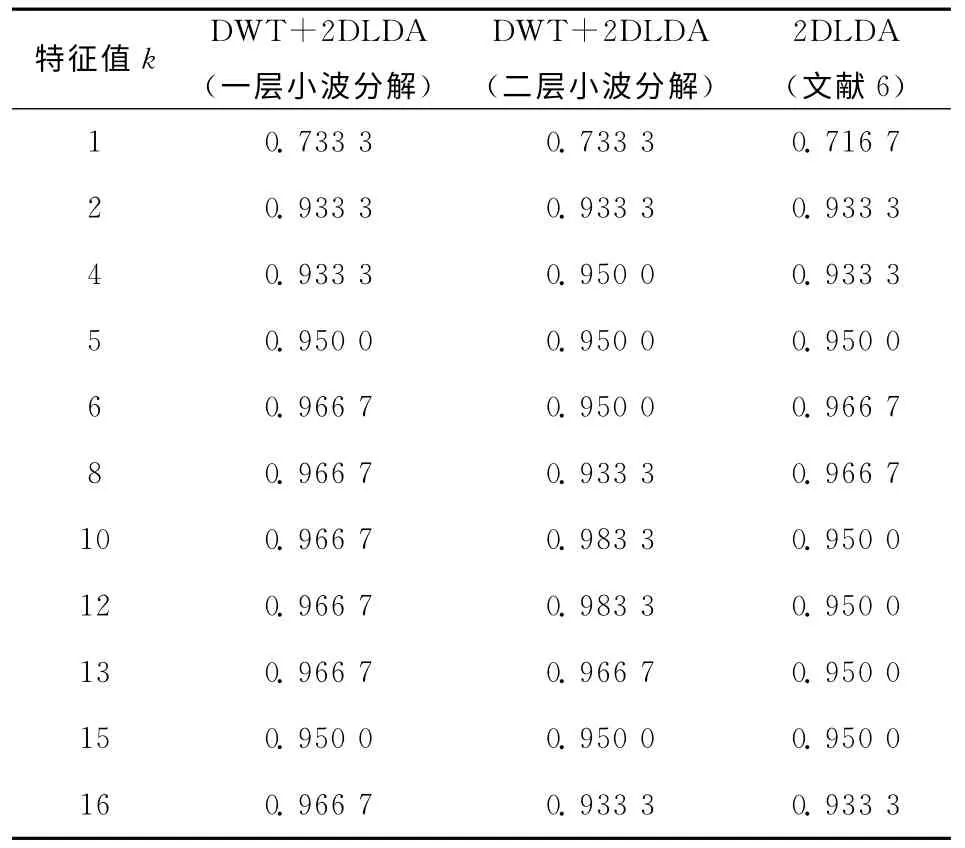
表1 实验测试数据Tab.1 The experimental test data

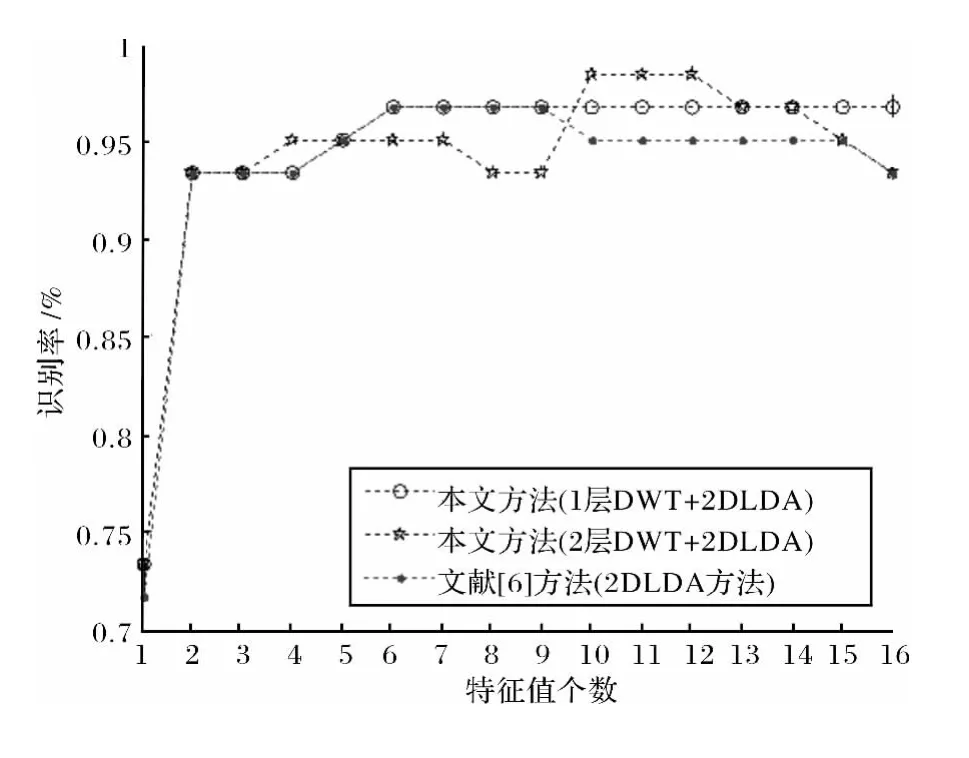
图3 人耳图像识别率对比结果Fig.3 The compared results of human ear image recognition rate

在相同的人耳图像库前提下，采用一层小波分解时，本文方法与2DLDA 方法的最高识别率都为96.67%，但是本文方法最高识别率范围高于2DLDA 方法，平均识别率也高于2DLDA 方法；采用二层小波分解时，本文方法的最高识别率达到了98.33%，高于2DLDA方法的最高识别率96.67%.实验结果表明，该方法识别效果优于2DLDA 方法.

4 结束语

2DLDA 是一种较好的生物特征识别的方法，也适合于人耳图像的识别.将人耳图像经离散小波变换后，提取保留了图片大部分信息的低频子带，去掉了人耳图像的一些细节和高频噪声的影响，也降低了维数，再在低频子带中采用二维线性鉴别分析方法，该方法对人耳角度变化和光照变化带来的影响有一定的免疫能力.实验结果表明，离散小波分解与2DLDA 相结合的方法在采用二层小波分解时，达到了最高识别率98.33%，是一种有效的识别方法.

［1］苑玮琦，柯 丽.生物特征识别技术［M］.北京：科学出版社，2009.

［2］赵海龙，穆志纯.基于小波变换和LDA／FKT 及SVM 的人耳识别［J］.仪器仪表学报，2009，30（11）：2273－2277.

［3］苑玮琦，郭伟芳，柯 丽.基于二维Fisher线性判别的人耳识别［J］.光电工程，2009，36（2）：133－136.

［4］邸继征.小波分析原理［M］.北京：科学出版社，2010.

［5］Xiong Huilin，Swamy M N S，Ahmad M O.Two－dimensional FLD for face recognition［J］.Pattern Reconition，2005，38（7）：1121－1124.

［6］Hua Yu，Jie Yang.A direct LDA algorithm for high－dimensional data－with application to face recognition［J］.Pattern Recognition，2001，34（10）：2067－2070.

［7］Li M，Yuan B.2D－LDA：a novel statistical linear discriminate analysis for image matrix［J］.Pattern Recognition Lett，2005，26（5）：527－532.

［8］吕秀丽，申 屠，洪 峰.基于2DLDA 与FSVM 的人耳识别［J］.科学技术与工程，2012，12（12）：2582－2584.

［9］袁 立，穆志纯，徐正光.基于人耳生物特征的身份识别［J］.模式识别与人工智能，2005，18（3）：310－315.