海南后水湾海域浅层粘土的工程地质特性评价
刘文涛 ,石要红,曾宁烽
(1.广州海洋地质调查局,广东 广州 510075;2.国土资源部海底矿产资源重点实验室,广东 广州 510075)
粘土是我国近岸海域一种重要的土质类型之一,广泛分布在海湾、泻湖、滨海平原等低能海洋环境区.全新世以来沉积的淤泥质粘土土质松软,具有高含水率、软塑或流塑状、高压缩性以及低抗剪强度等特征,而在南方近岸海域广泛分布的老粘土形成于晚更新世以前,土层经过压实作用,粘土结构紧密,压缩性低,抗剪强度显著增高,是较好的地基持力层[1].随着海底工程活动的日趋频繁,研究海底粘土的工程地质特性对区域内工程特性评价具有重要的意义.
后水湾位于海南岛西北部,琼州海峡西口,介于儋州湾与澄迈湾之间.湾口中央有邻昌岛和头排作为天然屏障,避风条件良好,是一个具有一定开发价值的天然海湾.后水湾属玄武岩台地海岸,多为基岩海岸.海岸的岬角和河溪入海口较多,沿岸多小海湾.湾内水深变化不大,5~12 m 水深占据海湾大部分区域[2].海域内沿岸工程开发活动较少,海域内浅部土层的工程特性研究亦较少.鉴此,本文利用后水湾外海域内的两口浅钻孔对其粘土的工程地质特性进行了分析和研究.
1 数据来源与分析方法
1.1 数据来源 广州海洋地质调查局分别于2011 年9 月和12 月对后水湾海域开展了2 次调查(见图1),获得40 m 浅钻两口,土工试验为42组,其中粘性土37 组,砂性土5 组.粘性土分析项目包括:含水率、土粒比重、密度、界限含水率、UU 三轴试验和室内压缩试验;砂性土分析项目有含水率、密度、土粒比重、颗粒分析.
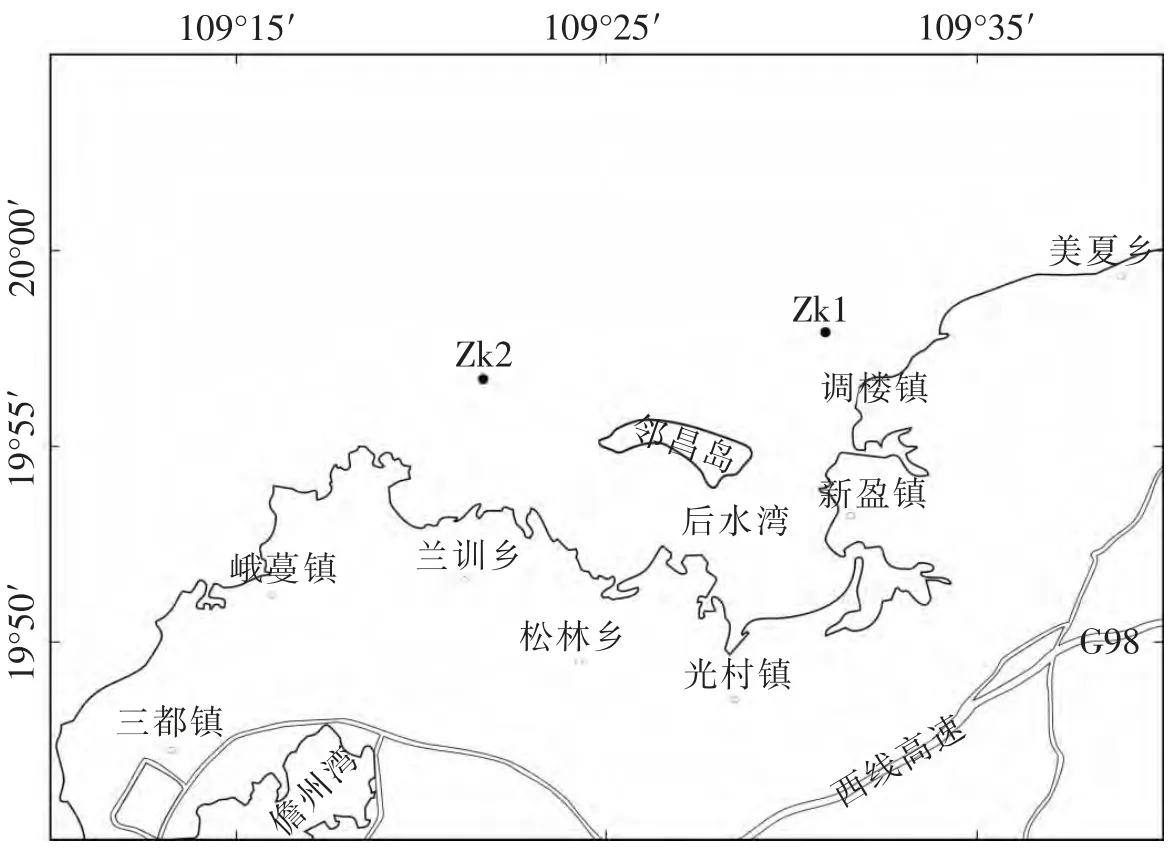
图1 研究区及钻孔位置示意图
1.2 分析方法 土体物理力学指标在垂向和水平方向上都存在着变异性[3],这种变异性是由多种因素造成的,其中土体本身内在的变异性是最主要的原因,其次取样、试验误差等多种随机因素也可造成这种变异性.通过概率统计的方法可有效地降低随机因素对土体特性带来的影响,有效地分析土体固有的变异性,并评价其工程地质特性.
国内外自20 世纪七八十年代就已经应用概率统计的方法对岩土参数的统计特性进行了大量的研究[4],相关分析、变异性分析和回归分析是常用的统计分析方法[5-13].本文运用变异性分析、相关性分析和回归分析计算了后水湾浅层粘性土的物理力学指标的变异系数和相关系数,初步探讨了区域内粘土的力学指标与物理指标间的回归方程.
2 浅层粘土工程地质特征

图2 ZK1 钻孔土层划分与主要物理力学指标垂向变化
2.1 土层划分及主要特征 研究区浅层土主要为高液限粘土(CH)和低液限粘土(CL).根据ZK1 和ZK2 揭示的土层,区域内浅层粘土可划分为3 层(见图2).3 层粘土分别以中砂(M)和角砾(G)层为分界层,厚0.5~1 m.第一层(表层)粘土以高液限粘土为主,含少量低液限粘土,青灰色或灰色,厚5.6~13.9 m,含水饱和,粘性强,含大量贝壳碎屑,呈软塑或流塑状,抗剪强度低,黏聚力平均为5.0 kPa,压缩性中等.在粒度组成上,粘粒含量略高于粉粒,粘粒含量随深度逐渐增加,由46.1%增加到63.8%,而粉粒含量则随深度减少,由51.7%减少到34.5%.砂粒含量极少,为1.2%~2.5%,顶部的含量相对较多.第二层粘土以高液限粘土为主,夹少量低液限粘土,棕黄色或灰色,厚19.3~23.7 m,局部夹粉砂薄层,含水率降低,呈可塑或硬塑状,抗剪强度较第一层明显提高,黏聚力平均为56.2 kPa,压缩性中等.在垂向上,粒度组成无明显变化,以粘粒和粉粒为主,粘粒略高于粉粒,上部砂含量相对较多;第三层粘土为低液限粘土,灰色,仅在ZK1 揭露其上层,厚9.3 m,可塑,抗剪强度较高,黏聚力平均为38.4 kPa,压缩性中等.
2.2 主要物理力学指标 表1 列出了后水湾海域三层粘土的物理力学指标范围,并对两个钻孔各层粘土的物理力学指标进行了统计.由表1 的统计结果可以看出,研究区浅层粘土的物理力学性质具有以下特点:
1 物理性质:表层粘土的含水率和孔隙比较高,第二层和第三层粘土的含水率和孔隙比明显降低,仅为第一层粘土的50%.表层粘土的天然密度较第二层和三层粘土略有降低,降低了10%~20%.表层粘土液性指数在1.07~2.05 之间,呈流塑状态.由于土粒间存在着天然的结构连接,样品在野外并未表现为流塑态.第二层粘土液性指数在0.08~0.58 之间,呈可塑或硬塑状态,以硬塑为主;第三层粘土液性指数在0.23~0.47 之间,亦呈可塑或硬塑状态.
通过对研究区内粘土物理指标的分析,可以看出,第二层和第三层粘土经过压实作用后,土体中水分被排出,颗粒排列更趋紧密,土体密度升高,稠度特征也由流塑变到可塑或硬塑.
2 塑性特征:区域内粘土的液、塑限值均较高,各层粘土变化区间较为接近(见表1);液限为34%~86.2%,塑限为17.4%~33.3%;区域内粘土的塑性指数较高,最高达54.7.塑性指数IP与粘粒含量和矿物成分有关,粘粒含量越多,亲水性大的矿物含量越高,IP也越大.塑型指数的特征反映出区域内粘土的物质组成基本一致,以亲水性粘土矿物为主.第二层粘土塑限指数的变化范围较大,这对土的工程性质的变化很有影响.
3 力学性质:沉积物的力学性质是指土在外力作用下所表现的性质,主要为变形特性和强度特性,通常以压缩系数和抗剪强度指标来表示,它是土的工程地质性质的主要组成部分.第二层和第三层粘土经过压实作用后,抗剪强度较第一层显著增加,压缩性降低,特别是粘聚力的变化最为明显,第一层粘土仅为2.00~6.90 kPa,而第二层和第三层为23.5~98.0 kPa.
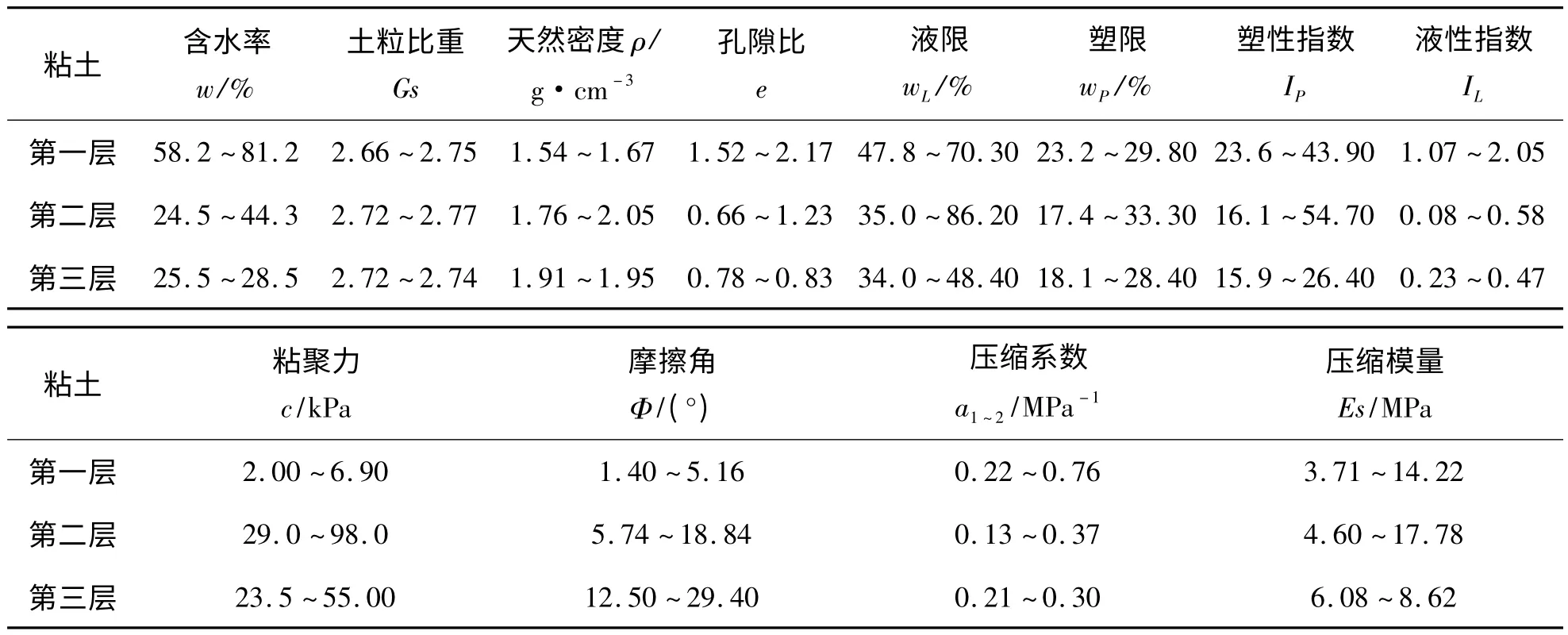
表1 后水湾海域粘土物理力学指标范围统计表
3 物理力学性质指标的数理统计
3.1 变异性分析 通过计算一组试验数据的变异系数(δ),可以了解土性指标的变异性大小.计算公式如下:

其中:σ—样品标准偏差;μ—样品平均值.
利用公式(1)计算了研究区内三层粘土的变异系数(见图3).由图3 可以看出,各层粘土的物理指标的变异性要普遍小于其力学指标.土粒比重的变异性最小,粘土的天然密度和饱和度的变异性也很低,变异系数小于0.04.第二层粘性土的物理指标的变异性要大于其上下两层,反映出该层工程地质特征的差异性较大.
粘土层的力学指标的变异性很高,其变异系数普遍大于0.3.由图3 可以看出,各层粘土力学指标的变异性随着深度的增加呈现逐渐降低的趋势.第一层粘土力学指标的变异系数变化范围为0.3~0.4,第二层粘土其变异系数的变化范围为0.27~0.33,第三层粘土力学指标的变异系数为0.12~0.33.
3.2 相关性分析 相关性分析是研究变量之间密切程度的一种统计方法,用相关系数表示.分析过程中,首先确定指标间的最佳数学关系模型,参照前人的研究经验,土体物理力学指标之间的最佳数学模型是线性关系模型[7].
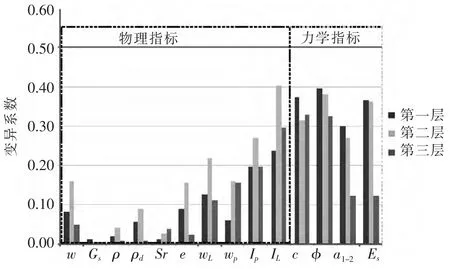
图3 研究区各层粘土变异系数柱形图
由表2 中可以看出,含水率与天然密度、干密度、孔隙比和液性指数之间存在高度的相关性,相关系数的绝对值在0.89 以上.含水率与天然密度、干密度呈负相关,而与孔隙比和液性指数呈正相关.土粒比重与其他物理指标间相关性较差,反映出土颗粒的组成与其所呈现的物理状态是没有直接关联的,这同样表现在液限、塑限、塑性指数与含水率、天然密度、孔隙比等指标间的相关性.土体的天然密度与其干密度、孔隙比和液性指数有着高度的相关性,相关系数的绝度值在0.832~0.982.
土体的物理状态可在一定程度上反映其力学性质,两者指标间存在一定的相关性.研究区粘土粘聚力与液性指数呈高度的负相关性,相关系数达-0.829,与含水率和孔隙比呈显著的负相关,而与其天然密度和干密度呈显著正相关.内摩擦角与含水率、天然密度、饱和度、孔隙比和液性指数等指标均呈现出一定的相关性.土体的压缩系数与其天然密度和干密度呈弱的显著负相关,与含水率、孔隙比和液性指数呈弱的显著正相关.与压缩系数相关性最好的是土粒比重,这主要是由于两者的数值变化范围均较小的原因.通过上述分析可以看出,研究区粘土的压缩系数和抗剪强度指标与含水率、天然密度、孔隙比等指标间的相关性特征呈现正负相反的相关关系.
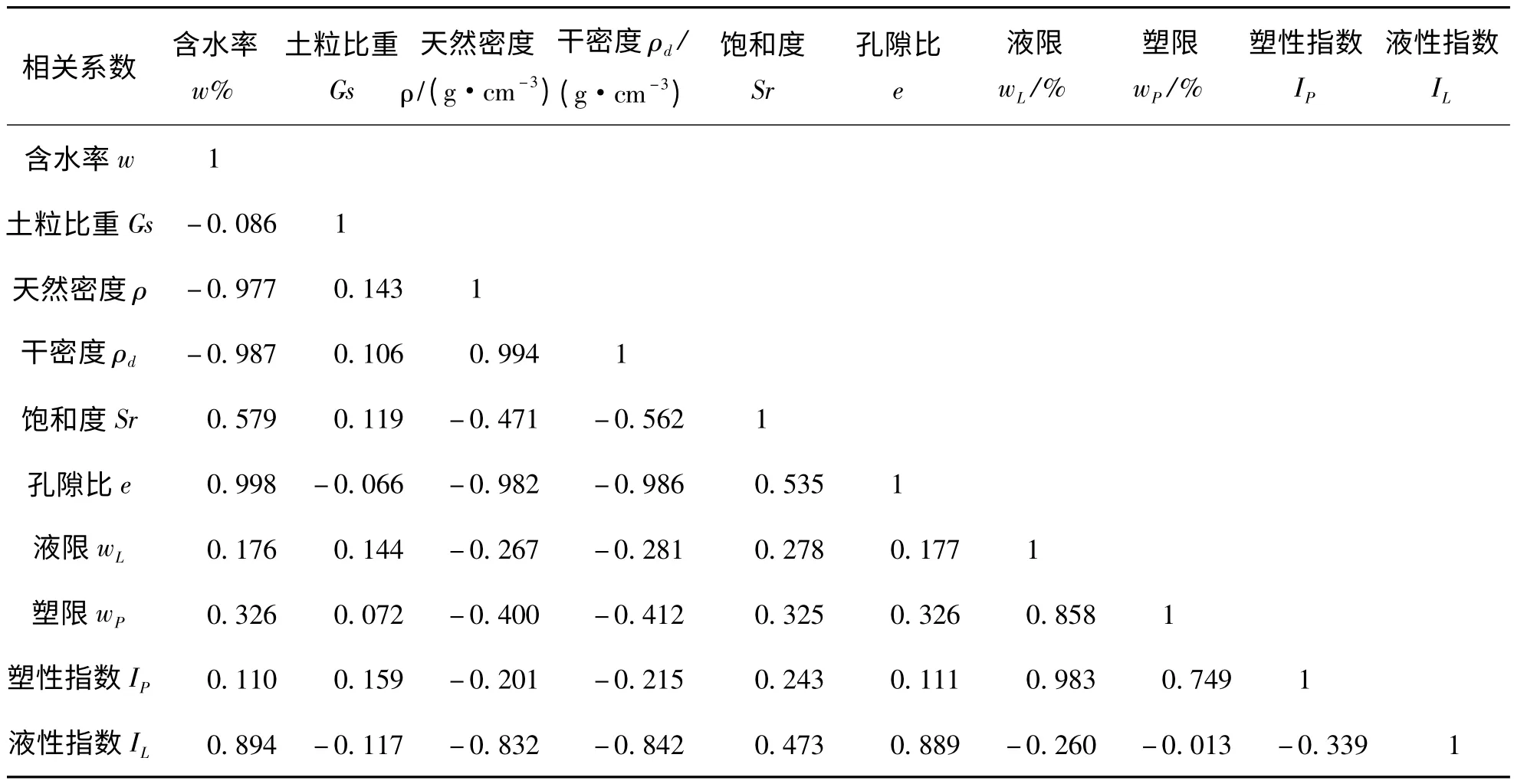
表2 后水湾粘土物理指标间相关系数的统计表

表3 后水湾粘土物理指标与力学指标间相关系数统计表
3.3 物理力学指标回归分析 在工程地质研究中,不容易直接获得力学性质指标,而对于物理性质指标,只要样品保存得当,都容易直接获得,并且两者存在内在的联系,例如粘性土的原始粘聚力取决于颗粒间距离的远近、土粒矿物成分、扩散层中的离子成分及土的密度;粘性土的内摩擦角取决于土的矿物成分、含水量、孔隙比、密度及形成历史等诸要素;压缩系数与土的类别、孔隙比、密度、含水量等因素有关.通过建立两者的回归关系,就可以简单地对各土层加以力学分析.
本文对区域浅层粘土进行了回归分析,在分析过程中,首先对实验数据描点作图,通过直观判断确定指标间的最佳数学关系模型.回归方程的显著性检验查相关系数表,显著性水平α 取0.05.物理力学指标的回归分析结果见表4.塑限及塑性指数与液限间成线性关系.相关系数大于显著性水平为0.05 时的临界相关系数值,回归方程显著.压缩系数与含水率、天然密度及孔隙比成较好的线性关系.相关系数也大于显著性水平为0.05 时的临界相关系数值.研究区内第一层粘土与第二、三层粘土的物理力学指标差异较大,在散点图中表层粘土样品与第二层与第三层粘土样品分属于不同的两个区域,整体上不呈线性相关.各种非线性曲线拟合中,以幂函数相关性最高.
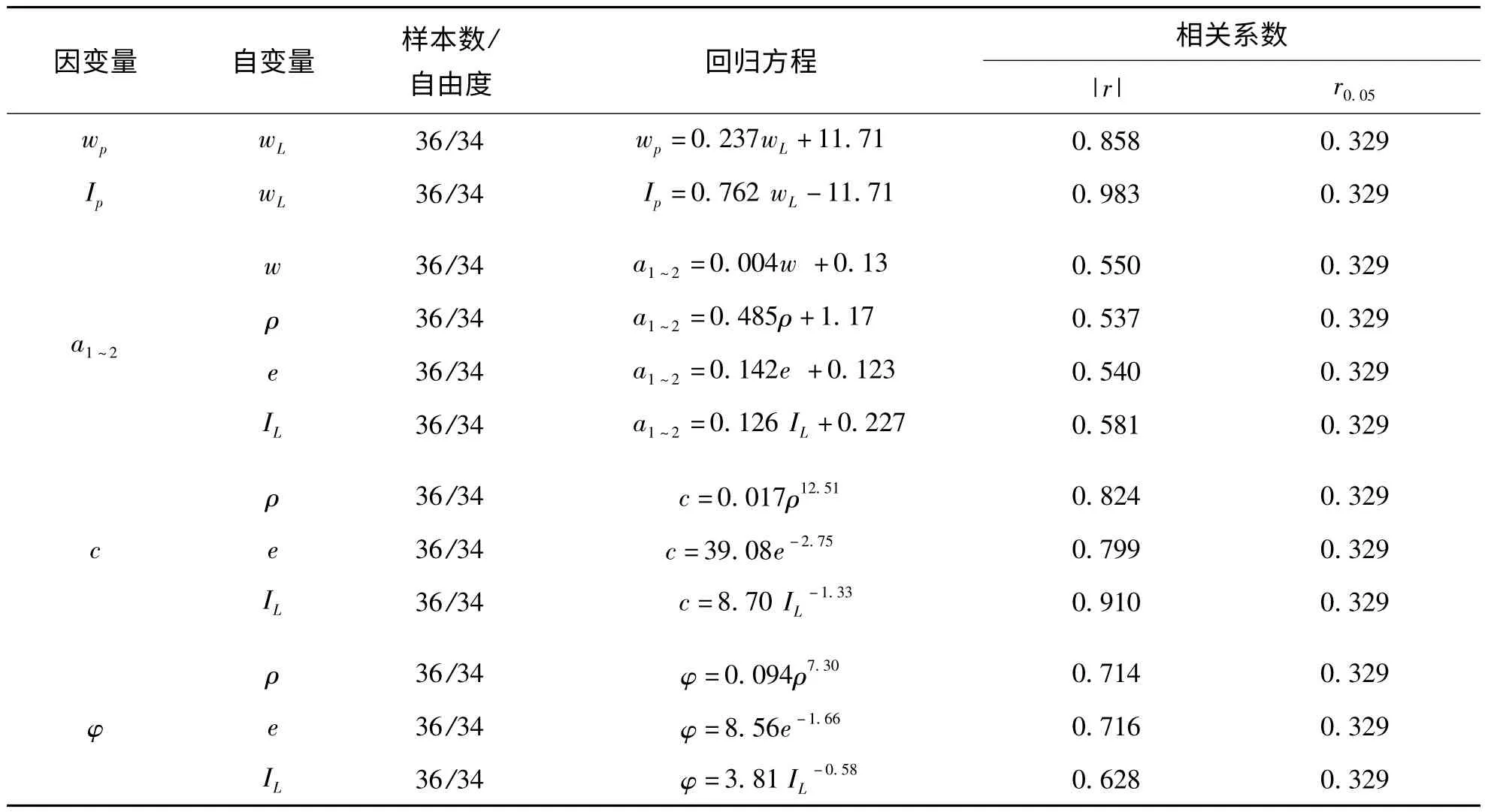
表4 物理力学指标间的相关关系
4 结论
(1)研究区内浅部土层可划分出3 层粘土层.三层粘土被中砂或砾砂(薄)层分隔.表层粘土与第二、三层粘土的工程地质特性存在显著差异.表层粘土的含水率、孔隙比较高,而天然密度较低,呈软塑或流塑态,抗剪强度较低,具有高压缩性;土层经过压实作用后,第二、三层粘土的物理力学性质发生了显著改变,含水率和孔隙比显著降低,而天然密度和抗剪强度升高,压缩性降低,稠度由软、流塑变到可塑或硬塑.
(2)研究区粘土的各物理指标的变异性普遍小于其力学指标的变异性.第二层粘土的物理指标的变异性大于其上下两层,反映出该层工程地质特征的差异性较大;力学指标的变异性随深度的增加而逐渐降低.
(3)研究区内粘土的含水率、天然密度、干密度、孔隙比和液性指数之间存在显著的相关性,土粒比重、液限、塑限及塑性指数与其他物理指标间相关性较差.其压缩系数和抗剪强度指标与含水率、天然密度、孔隙比等指标间的相关性呈现正负相反的相关关系.
(4)通过对研究区粘土物理力学指标的回归分析,得到了研究区主要物理力学指标的回归方程;研究区内粘土的压缩系数与含水率、天然密度、孔隙比及液性指数成较好的线性关系;黏聚力和内摩擦角与天然密度、孔隙比及液性指数间呈曲线相关,以幂函数拟合度最高.
[1]郑志昌,陈俊仁,朱照宇.南海海底土体物理力学特征及其地质环境研究[J].水文地质工程地质,2004(4):50-53.
[2]《中国海湾志》编纂委员会.中国海湾志:第11 分册[M].北京:海洋出版社,1999.
[3]高大钊.土力学可靠性原理[M].北京:中国建筑工业出版社,1989.
[4]李小勇.土工参数空间概率特性及软粘土地基固结概率分析[D].杭州:浙江大学岩土工程研究所,2001.
[5]高大钊.地基土力学性质指标的可靠性分析与取值[J].同济大学学报:自然科学版,1985,25(4):59-67.
[6]PHOON,Kok-kwang,KULHAWY Fred H.Characterization of geotechnical variability[J].Canadian Geotechnical Journal,1999,36 (4),612–624.
[7]阙金声,陈剑平,石丙飞.广州大学城软土的工程地质性质统计分析[J].煤田地质与勘探,2007,35(1):49-52.
[8]王振红,潘永坚,潘国富,等.舟山—岱山间西部海域第四纪海底沉积物物理力学指标统计分析[J].海洋通报,2011,30(5):557-561.
[9]KIM Donghee,KIM Kyu-sun,KO Seongkwon,et al.Assessment of geotechnical variability of Songdo silty clay[J].Engineering Geology,2012,133-134:1-8.
[10]阮波,冷伍明.粘性土物理力学指标的统计分析[J].大坝观测与土工测试,1998,22(1):5-7.
[11]刘春,白世伟,赵洪波.粘性土土性指标的统计规律研究[J].岩土力学,2003,24(增刊):180-184.
[12]吕小飞,叶银灿,潘国富.杭州湾浅层粘性土物理力学指标的统计分析[J].海洋学研究,2005,23(4):8-14.
[13]冯秀丽,林霖,庄振业,等.现代黄河水下三角洲全新世以来土层岩土工程参数与沉积环境之间的关系[J].海岸工程,1999,18(4):1-7.

