全微分法在微分学中的应用
蔡白光,郭纪云
(海南大学 信息科学技术学院,海南 海口 570228)
一元函数的导数与多元函数的偏导数是大学数学的重要内容,也是很多初学者较难掌握的知识点.一方面,函数本身的多变性和复杂性,特别是不少复合函数变量之间错综复杂的关系,使学生在解决这类问题的时候捉襟见肘;另一方面,学生单一地依据求导法则去求解隐函数,复合函数的(偏)导数的时候,常会发现很难把握住函数变量间的关系,从而很容易造成问题的错解.为此,本文提出应用全微分法去解决函数的(偏)导数问题.该方法的好处在于:不论函数的形式如何多样,变量之间的关系有多么复杂,都可以利用一阶微分形式的不变性对变量进行同等处理,从而可使问题简单化,思路清晰化和方法规范化,大大提高了求解的效率,避免了繁杂的链式过程.
1 全微分法
所谓全微分法就是运用函数的全微分形式不变性,在函数或隐函数组中的各方程两端分别求全微分,必要时消去中间变量的微分,最终求得函数的微分,并由此解出函数的导数或偏导数.
一元函数及二元函数的全微分不变性可以概括为下列两个定理.
定理1 设函数y=f(x)可导,则无论x 是自变量还是中间变量,函数y=f(x)的微分形式总是dy=f'(x)dx,即一个一元可微函数的微分总是等于该函数对某个变量的导数乘以该变量的微分.
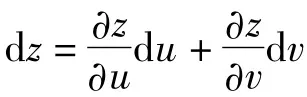
一般地,定理1 和定理2 可以推广到任意n 元可微函数.
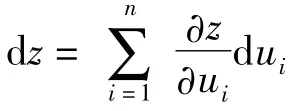
2 全微分法在微分中的应用
2.1 全微分法在参数方程求导中的应用
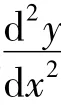
解 分别对x,y 用全微分形式不变性及微分性质得

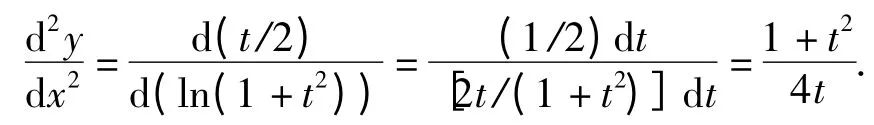
2.2 全微分法在多元复合函数及隐函数求导中的应用
分析 该题目属于复合函数求偏导问题,z 与x,y 的关系非常明确,但是,仍会有同学纠结于x 与y 之间的关系,这会让问题变得复杂,且不利于求解问题.而采用全微分法则不需要考虑它们之间的关系,从而可使问题变得简单.




即
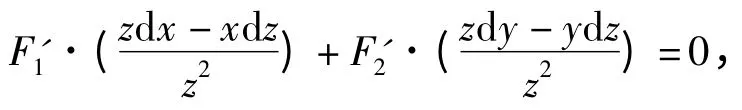
整理可得

所以
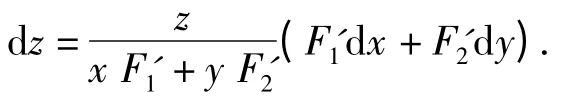

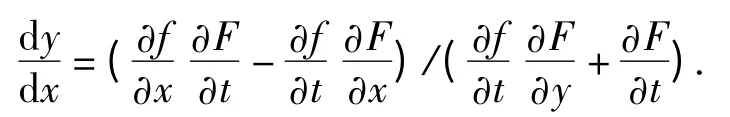
证 利用全微分法,对函数y=f(x,t)和方程F(x,y,t)=0 两边分别求微分,得

联立上面两式消去dt,整理可得

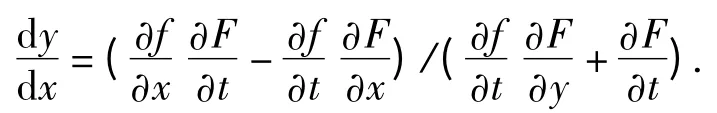
运用以上思路,同样可以应用全微分法到由多个方程所确定的隐函数组中的导数求解问题中去.通过对各个方程进行微分,可从所得到的微分方程组中求解出待求解的函数的导数(偏导数).
3 结论
全微分法不仅是函数求导的链式法则的有利补充,同时更是求解复合函数、抽象函数、方程所确定的隐函数以及由方程组所确定的隐函数组的(偏)导数的非常简洁、便利、规范和高效的一种数学方法.该方法的引入使函数求导问题变得“有法可依”,“简单易解”,从而大大提高了解决这类问题的效率,让函数求导问题不再成为我们学习微积分的难题.
[1]同济大学数学教研室.高等数学[M].北京:高等教育出版社,1993.
[2]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.
[3]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,1993.

