重力坝分析的改进有限元等效应力法
杨会臣,贾金生,郑璀莹
(中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038)
1 改进的有限元等效应力法
有限元等效应力法由我国学者首先提出[1-4],其基本思想是将某一截面上有限元计算的应力结果等效为作用在该截面上的一组内力,然后利用材料力学的方法计算截面上的应力分布,以避免角缘处有限元计算结果的应力集中。有限元等效应力法分析拱坝的文献[5-7]很多,但用于研究重力坝应力分布的文章还比较少[8-9]。
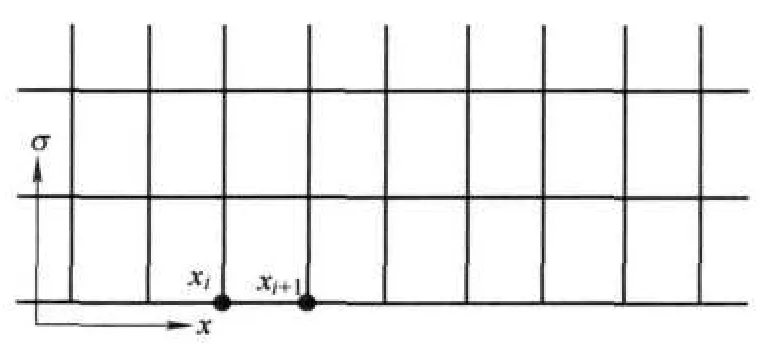
图1 有限元应力计算网格
对于图1所示的有限元计算网格,xi处的竖向正应力为,xi+1处的竖向正应力为,则该截面上的等效内力为[8]:

式中:N为截面轴力;M为截面弯矩;x0为截面转动中心;li=xi+1-xi;B为截面宽度,取1。根据材料力学偏心受压构件正应力计算公式,结点i处的有限元等效应力即为:

其中:L为截面长度;I为截面绕x0的转动惯量。
在利用式(2)进行取矩计算时,将合力的作用点作用在两结点的中点,其默认了一个假定,即两结点之间应力是相等的,即矩形分布,而实际应力分布是一个梯形,根据实际的应力分布,修改式(2)如下:

为了研究改进前后等效应力计算结果的差异,选取某重力坝进行了分析。重力坝断面和有限元网格如图2所示,计算中仅考虑了坝体自重和静水压力,上、下游水位如图2(a)所示,采用平面四结点单元对坝体-地基系统分析,基础范围在上、下游及深度方向取3倍坝高,采用两种有限元网格,其中图2(b)坝体单元尺寸为2m,图2(c)坝体单元尺寸为5m。坝体和地基材料参数见表1。

表1 坝体、地基材料参数

图2 某重力坝有限元网格
采用改进前后两种算法对上述重力坝进行有限元等效应力计算,计算结果见表2。从表2可以发现,原算法由于取矩中心选在两个结点中心,造成力矩偏小,等效后的内力弯矩项偏小,特别是当网格尺寸较大时,对计算结果影响更大。

表2 不同单元尺寸下算法改进前后计算结果对比
2 有限元等效应力法与材料力学方法应力计算结果的比较
已有研究[9]考虑了等效阶次、网格尺寸、取矩中心和层面高度[8]等的影响,但是未见等效后的应力与材料力学计算结果的比较。为此,利用改进的有限元等效应力计算方法计算某重力坝建基面的竖向正应力,并与材料力学结果进行对比,以便基于现行的重力坝设计规范规定的应力标准,利用有限元等效应力结果进行重力坝坝体安全度的评价。
利用有限元方法、材料力学方法和改进有限元等效应力方法计算所得的建基面竖向正应力如图3所示。

图3 不同方法计算所得建基面竖向正应力的比较
从图3可以发现,有限元等效应力法与材料力学法结果基本一致,均呈线性分布,避免了角缘处有限元计算结果的应力集中现象。但是,有限元等效应力与材料力学结果有一定差异,这与材料力学假定基础为刚性有关。
3 地基刚度对建基面竖向正应力分布的影响
为了研究地基刚度对有限元等效应力与材料力学计算结果差异的影响,对不同弹性模量的地基进行有限元等效应力分析,地基刚度与初始刚度的比值见表3。
采用式(4)计算截面弯矩,计算结果见图4、图5。坝踵、坝趾处竖向正应力随地基刚度变化如图6所示。由图4—图6可见,有限元等效应力能够反应地基刚度对建基面竖向正应力分布的影响,且地基刚度越大,越接近材料力学的计算结果。

表3 地基刚度变化

图4 地基刚度对有限元等效应力的影响

图5 有限元等效应力与材料力学结果的比较

图6 坝踵坝趾处竖向正应力随地基刚度的变化
有限元等效应力法避免了有限元角缘应力集中的同时,解决了材料力学无法考虑地基刚度对坝体应力分布影响的问题。
4 工程应用
守口堡工程位于黑水河上游段,最大坝高60.6m,为我国第一座胶结颗粒料永久工程。守口堡工程坝址处强风化层厚0.90~5.00m,弱风化层厚4.30~8.75m,弱风化层下限高程为1174.539~1186.170m。
胶结颗粒料坝是由胶凝材料胶结颗粒料筑成的坝,是对传统土石坝、砌石坝及混凝土坝等筑坝技术构成的筑坝技术体系的有益补充。曾用的中英文名称包括:胶凝砂砾石坝、贫胶渣砾料碾压混凝土坝、贫胶粗粒料坝、硬填料坝、超贫胶结材料坝、CSG Dam、Hardfill Dam、Trapezoidal CSG Dam等。胶结颗粒料坝强调“宜材适构”理念,注重就地取材、减少弃料、快速施工、易于维护、节能环保和经济。该坝型具有经济、快速、安全和环保等优点,在我国具有广泛应用前景。
由于较大的坝体断面,有限元方法更适宜分析胶结颗粒料坝的应力分布。相比于传统重力坝,胶结颗粒料坝应力分布更加均匀,然而由于有限元计算结果的应力集中,计算结果不能很好地评价坝体坝踵、坝趾处的应力情况。为此,利用改进的有限元等效应力方法对坝体进行应力分析,以合理评价不同基岩条件下坝踵坝趾处的竖向正应力。
胶结颗粒料坝对基础有较强的适应性,可适当放宽对基础处理的要求。对于不同的基岩条件,计算守口堡胶结颗粒料坝的应力情况,以确定对不同基岩的适应情况。坝体及基岩参数取值[10]见表4。

表4 坝体与基岩材料参数
对于不同基岩条件,选取上、下游等坡比1∶0.5的坝体断面,采用有限元等效应力方法对坝体的受力特性进行分析。坝体有限元模型如图7所示。
坝趾处竖向正应力的有限元结果与有限元等效应力结果见表5。分析计算结果发现,有限元等效应力法能够反映地基刚度对建基面竖向正应力分布的影响,不同的基岩条件下,坝趾处竖向正应力的有限元等效应力为1MPa左右的压应力。

图7 守口堡工程断面及有限元模型

表5 坝趾处竖向正应力的有限元结果与有限元等效应力结果对比
5 结论
等效应力法分析重力坝是可行的,与规范中的材料力学方法得出的结果有较好的对应关系。对等效应力算法中的等效弯矩的计算方法进行改进后,取矩中心更加科学合理,等效应力计算取得了更高的精度。有限元网格尺寸较大时,精度提高更加明显。等效应力法能够反映地基刚度对建基面竖向正应力分布的影响,从而解决了材料力学的一些限制。对比有限元等效应力结果与材料力学计算的应力结果发现,材料力学对刚性地基的假设,使得坝踵处的应力偏大,是保守的和偏于工程安全的。
[1]朱伯芳.混凝土坝计算技术与安全评估展望[J].水力水电技术,2006,10(37):24-28.
[2]朱伯芳.国际拱坝学术讨论会专题综述[J].水力发电,1988(8):49-52.
[3]朱伯芳.拱坝的有限元等效应力及复杂应力下的强度储备[J].水利水电技术,2005(1):43-47.
[4]傅作新,钱向东.有限单元法在拱坝设计中的应用[J].河海大学学报,1991,19(2):8-15.
[5]李同春,章杭惠.改进的拱坝等效应力分析方法[J].河海大学学报,2004,32(1):104-107.
[6]肖伟荣,苏志敏,唐涛.有限元等效应力方法在拱坝设计中的应用[J].云南水力发电,2005,21(1):36-39.
[7]SL 282-2003,混凝土拱坝设计规范[S].
[8]范书立,陈健云,郭建业.有限元等效应力法在重力坝强度分析中的应用[J].水利学报,2007,38(6):754-760.
[9]杨强,刘福深,周维垣.基于距法的重力坝建基面非线性等效应力分析[J].水利发电,2006,32(2):23-25.
[10]SL319-2005,混凝土重力坝设计规范[S].

