邓肯E-B模型参数敏感性分析
杨玉生,刘小生,赵剑明,汪小刚
(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100048;2.水利部水工程建设与安全重点实验室,北京 100048)
1 研究背景
在土石坝设计和安全评价中数值分析占有重要地位,但其结果的可靠性,主要取决于计算中所采用的土体本构模型是否能正确反映材料的应力应变关系及强度特性,以及确定的模型参数是否反映原位土体的情况。但要建立起考虑所有影响因素,适合于所有土类及问题的统一模型是不现实的。必须针对不同的土类及不同的问题,考虑主要影响因素,采用不同的土体本构模型。同时,更重要的是对于选定的土体本构模型,合理地确定模型参数。
邓肯E-B模型是国内外土石坝工程领域应用最广的土体本构模型,通常采用室内三轴试验确定其参数。但对于覆盖层和大粒径坝料,单纯依靠室内试验难以准确确定其工程力学参数。近年来,联合室内和现场原位试验,借助反分析技术确定覆盖层和大粒径坝料工程力学参数的方法日益受到关注。反分析中,待反演参数过多会导致反演精度降低,且反演结果可能出现多值问题[1]。因此,需要合理选取待反演的模型参数,也就有必要确定邓肯模型参数的敏感性,目前已有部分研究者对此做过有益探讨[2-7]。但对影响敏感性分析结果的因素探讨较少,且对于同一问题,不同研究者给出的参数敏感性分析结论差异较大。如文献[3]给出的堆石坝参数敏感性排序为n、m、K、Kb,文献[4]认为Kb、φ0、K对位移的敏感性较强,文献[5]给出的水平位移参数敏感性排序为n、K、m、Rf,竖直位移参数敏感性分析排序为Kb、m、Δφ、n,文献[6]认为水平位移对φ0、n、Rf的敏感性较强,竖直位移对Kb、φ0、n、m的敏感性较强。这种对同类构筑物分析结论的差异,迄今尚没有人给出合理解释,这也说明对应用于土石坝的邓肯E-B模型参数的敏感性还没有达成共识。
对邓肯模型E-B模型参数进行敏感性分析时,在样本空间和目标位移值的选择上,一般有两种方法:一是将全体节点作为样本空间,同时将全体节点中的最大变形值作为敏感性分析的目标评价对象;二是选择个别节点作为样本空间,并将这些节点对应的位移作为目标评价对象。采用所有样本点的宏观位移表现(即最大位移)作为敏感性分析的目标评价值时,由于模型参数的非线性,很难将参数变化率与位移变化率对应起来。由于土石坝结构复杂且三维空间效应明显,其位移变化十分复杂,样本空间仅包含个别节点时,样本空间的大小和样本点的选择是否会影响参数敏感性分析结论,尚没有人进行讨论。因此,采用少量样本点进行参数敏感性分析,其结论是否具有代表性亦存在疑虑。本文结合某高土石坝工程,对应用于土石坝的邓肯E-B模型参数进行敏感性分析,考察影响参数敏感性分析结果的因素,确定邓肯E-B模型各参数的敏感性,为反演分析时合理选取待反演参数提供依据。
2 单个参数变化时的敏感性分析
某水电站拦河大坝为混凝土面板堆石坝,坝高110m,坝体典型断面见图1所示。分区坝料的邓肯E-B模型参数见表1所示。对不同的坝体分区,可分别进行模型的参数敏感性分析。此处假定大坝土石料为同一种材料,以主堆石区的模型参数为基准参数,在基准参数基础上分别增大或减小各参数(见表2),进行敏感性分析,并采用位移变化率(参数变化时节点位移增量与基准参数下相应节点位移值之比)衡量参数的敏感性。坝体和地基网格划分见图2。整个坝体共划分为6189个单元,包含8163个节点,坝体的填筑和面板浇筑共分为15级。基准值下坝体典型断面位移分布见图3。

图1 某高堆石坝典型断面

图2 坝体-地基网格划分

表1 某高土石坝坝体不同分区材料设计参数

表2 单个参数变化时敏感性分析方案
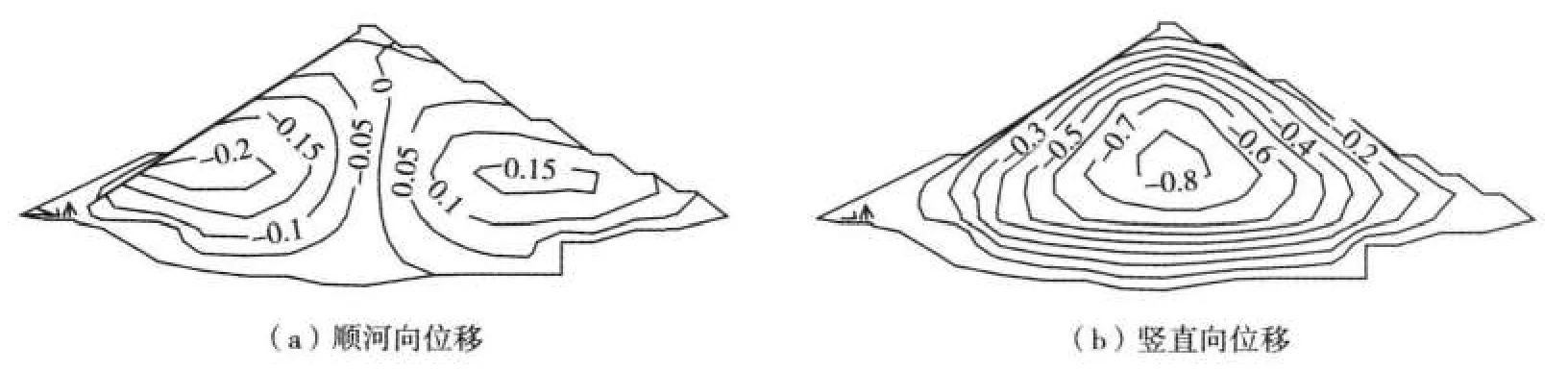
图3 基准值下察汗乌苏面板堆石坝典型断面位移分布(单位:m)
2.1 Et中各参数的敏感性邓肯E-B模型的切线弹性模量表达式为:

式中:Rf为破坏比;S为应力水平;K、n为试验常数;C、φ为线性强度参数;pa为大气压力。
对无黏性粗粒土来说,C=0,在高土石坝数值分析中常采用非线性强度参数:

因此,对无黏性粗粒土来说,Et式中共有Rf、φ0、Δφ、K、n共5个参数。
(1)Rf变化。破坏比Rf是反映土体抗剪强度发挥程度的量。Rf越大,计算采用的抗剪强度越接近土的理论极限抗剪强度,土体的抗剪强度发挥程度越大,反之亦然。Rf减小33%时,坝体位移变化率(参数变化时节点位移增量与基准参数下相应节点位移值之比)在顺河向集中在-20%~-40%,在竖直向集中在-5%~-15%。
(2)φ0和Δφ变化。φ0和Δφ为非线性强度参数,φ0减小时,强度参数φ减小,Δφ减小时,强度参数φ增大。这里仅给出φ0减小时的结果。φ0减小33%时,位移变化率在顺河向多为100%~300%,有的部位甚至达到500%,在竖直向多为20%~60%。
(3)K和n变化。K减小33%时,位移变化率在顺河向为30%~100%左右,在坝体断面中心部位集中在40%~70%;在竖直向多为10%~30%,坝体断面中心部位竖直向的位移变化率集中在10%~20%之间。K增大时,坝体变形的变化趋势与K减小时相反,量值上有一定差异。
n值增大33%时,位移变化率在顺河向集中于-15%~-20%,在竖直向集中于-5%附近,坝体变形趋于减小。n减小时,坝体变形趋于增大。
2.2 Bt中各参数的敏感性切线体积模量B采用下式计算:

式中:Kb为体积模量系数,为试验常数,其值为σ3=100kPa时的切线模量B,但无量纲;m为体积模量指数,为试验常数。
Kb和m变化时,顺河向位移变化比较复杂,上游侧和下游侧均既有正向位移发生,又有负向位移发生。限于篇幅,仅给出Kb增大33%时顺河向位移变化率和位移增量矢量分布图(见图4)。

图4 Kb变化时顺河向的位移变化率(单位:%)
由图4(a)可见:(1)Kb增大33%时,顺河向位移变化率在0.4H(H为坝高)以上为正,集中在10%~30%,在0.4H以下为负,集中在-10%左右。由图4(b)可见:Kb增大时,位移增量矢量在0.4 H以下指向坝轴线,在0.4H以上背离坝轴线,即坝体上部变形趋于增大,下部变形趋于减小。Kb减小33%时,顺河向位移变化率和位移增量矢量变化趋势与Kb增大33%时相反,量值上有一定差异。
因此,Kb变化时,坝体不同部位的位移变化较复杂,在坝体顺河向反映最明显。不同部位位移增量的大小和趋势差异较大,进行敏感性分析时,所选择的样本点不同,可能影响敏感性分析的结论。
2.3 变化单个参数时的敏感性分析结果某个参数变化时位各节点位移变化率的情况还可以图5所示的点集形式表示。图5包含了网格所有节点的位移变化率,但对于基准值小于一定值(比如5cm)的节点,本文在分析时不予考虑。由图5可知,位移变化率的变动范围存在一个分布比较密集的条带,为比较不同参数变化引起的位移变化率的大小,近似取条带中间部位的位移变化率作为代表值,则可汇总如表3所示。由表3可见:(1)顺河向位移对参数K、φ0、Rf、n较敏感,竖直向位移对K、Kb、Rf、φ0较敏感;(2)坝体变形的变化趋势与K、n、φ0的变化方向相反,即K、n或φ0增大时,坝体变形减小,K、n或φ0减小时,坝体变形增大;坝体变形的变化趋势与Δφ0、Rf的变化方向一致,即Δφ0或Rf增大时,坝体变形增大,Δφ0或Rf减小时,坝体变形减小。
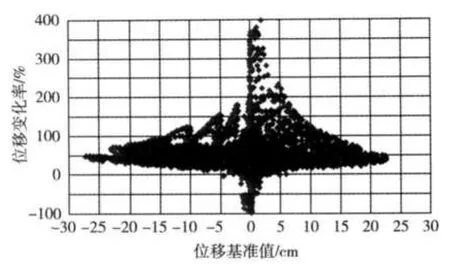
图5 K减小33%时顺河向位移变化率

表3 单个参数变化引起的位移变化率(单位:%)
需要指出的是,已有的研究表明,模型参数对位移的影响具有强烈的非线性[7-8]。因此参数变化的幅度可能会影响分析的结论。针对不同的工程问题,需要依据材料参数的试验变化范围,选定合适的参数基准值和变化幅度。
3 多个参数变化时的敏感性分析
3.1 正交表和参数水平设置文献[4]曾采用正交设计的方法对邓肯E-B模型参数的敏感性进行过分析,为便于与文献[4]的已有研究结果比较,本文采用与其相同的正交设计表L18(21×37)和参数水平设置,见表4。

表4 方案1的参数水平
在表4参数水平的基础上,结合表1中材料参数的变动范围,分别设置不同的参数水平(见表5),以对比分析参数水平设置的不同对参数敏感性分析结论的影响。表5中“相对于方案N-1变化的参数”,指方案N仅在方案N-1的基础上变动了某一个或两个参数水平的设置。如方案2仅在方案1的基础上调整了K值的参数水平设置,方案3仅在方案2的基础上调整了Kb的参数水平设置。

表5 各方案在方案N-1基础上调整的参数
3.2 确定参数敏感性的方法敏感性分析的样本空间选定为坝体各参与计算的节点,目标评价对象为各点的计算位移值,但不统计受到约束或变形量过小的节点,包括:(1)固定边界点;(2)某一方向受到约束的节点;(3)坝体表面节点;(4)级差过小的节点。参数敏感性的确定包含两个步骤:(1)采用级差确定各点的参数敏感性排序;(2)将各节点参数敏感性排序进行汇总统计,分析各参数敏感性排序占参与统计节点的比例。
3.3 敏感性分析结果表6给出了方案1下的敏感性分析结果:顺河向第一敏感因素排序为φ0、Kb、n、K,其对应的节点个数分别为5070、795、254、135;第二敏感因素排序为K、n、Kb、φ0,对应的节点个数分别为2221、1952、1091、602。因此,按照方案1进行敏感性分析时,影响顺河向水平位移的参数的敏感性排序为φ0、Kb、n、K,而Rf、Δφ0、m和ρ对顺河向位移影响较小。同样分析可得,影响坝轴向位移的参数敏感性排序为Rf、φ0、Kb、Δφ0、n、m、K;影响竖直向位移的参数的敏感性排序为Kb、φ0、Rf、K、Δφ0、m、n。按照方案1—4进行敏感性分析的结果汇总于表7和表8。

表6 方案1参数敏感性分析结果

表7 方案1和方案2的分析结果

表8 方案3和方案4的分析结果
4 影响敏感性分析结果因素的讨论
文献[4]采用正交设计对邓肯模型参数敏感性分析的结果见表9。本文方案1与文献[4]采用的正交表和参数水平设置完全相同,不同的是文献[4]进行敏感性分析的样本空间仅包含两点,而本文包含了除去坝表面和固定边界部位的所有节点。

表9 文献[8]中的敏感性分析结果[8]
对比表7中方案1和表9可知,分析结果差异很大。由表6可知,若以单个点而论,每一个参数都有作为第1或第2敏感性因素的可能。这说明文献[4]以个别样本点的位移作为目标评价值,得到的相应结论对于所选定的样本点来讲是可能的;同时也说明,以坝体个别节点的位移作为目标评价值进行参数敏感性分析时,分析结论可能会随样本点选择的不同而变化。
而对本文来说,由于样本点数量充足,以各个样本点位移为目标评价值,再统计影响各样本点的敏感因素,这种方法无疑较个别样本点获得的结果更合理。如对于顺河向位移,本文的分析结果显示参与统计的6 437个节点中,有5 070个节点的第一敏感因素为φ0,占参与统计的节点的79%,其次为Kb、n、K,三者作为第1敏感性因素的节点共占参与统计的节点的18%。
由表7和表8可知,不同参数水平设置情况下,分析获得的敏感因子排序不同,说明参数水平的设置会影响敏感性分析的结果。方案3中,各水平下不同参数的变化率基本一致,因此,以方案3的结果作为多个参数变化时敏感性分析的结果。即顺河向位移对K、φ0较敏感,对Kb、n和m的敏感性较弱;坝轴向位移对各参数敏感性相当,这也从侧面说明了坝轴向位移变化的复杂性。竖直向位移对K、Kb较敏感,对n、m的敏感性较弱。
单个参数变化时的参数敏感性分析结论与同时变动多个参数的敏感性分析结论基本一致。综合两种参数敏感性分析结果,可以获得如下认识:(1)坝体不同部位、不同方向的位移对相同模型参数,敏感性不同。因此,样本点的选择可能影响敏感性分析的结论。在参数敏感性分析时,若以个别样本点的位移作为目标评价值,则应根据一般经验选择坝体可能发生较大变形的点作为样本点,但样本点数量不宜过少。(2)参数水平的设置是影响分析结论的重要因素,在进行参数敏感性分析时,应结合室内土石料室内试验获得的参数变化范围确定合理的参数水平设置。
5 结论
采用邓肯E-B模型,本文对土石坝应力变形计算进行了参数敏感性分析研究,对影响分析结果的因素进行了讨论,给出了邓肯E-B模型参数的敏感性排序。其主要结论:(1)坝体不同部位、不同方向的位移对相同模型参数,敏感性不同。正交设计用于敏感性分析时,样本点的选择可能影响分析结论,参数水平的设置也是影响分析结论的重要因素。在参数敏感性分析中,样本点选择的差异或参数水平设置的不同是导致对同一类型构筑物参数敏感性分析结论迥异的原因;(2)为保证获得合理的敏感性分析结论,应注意选择坝体不同部位位移较大的一些节点作为样本点,同时应结合土石料室内试验获得的参数变化范围进行参数水平设置,并使不同参数相邻水平的变化率基本一致;(3)敏感性分析表明,坝体变形的变化趋势与K、n、φ0的变化方向相反,与Δφ、Rf的变化方向一致,Kb、m对坝体变形的影响复杂,不同部位、不同方向的变形趋势甚至相反;(4)在模型参数的合理变化范围内,在参数变化率相同或相近的情况下,邓肯E-B模型的参数敏感性如下:顺河向位移对K、φ0较敏感,对Kb、n的敏感性次之,对m,Rf的敏感性弱;竖直向位移对K、Kb、φ0、Δφ、Rf较敏感,对n、m的敏感性较弱。
[1]杨志法,王思敬,冯紫良,等.岩土工程反分析原理及应用[M].北京:地震出版社,2002.
[2]何昌荣,杨桂芳.邓肯模型参数变化对计算结果的影响[J].岩土工程学报,2002,24(2):170-174.
[3]恩戈科.堆石坝材料参数的灵敏度分析[J].河海大学学报,1999,27(5):94-99.
[4]牟声远,王正中.堆石料邓肯模型的参数敏感性与统计分析[J].中国农村水利水电,2009(3):97-100.
[5]李金凤.高面板堆石坝堆石体力学参数反演及变形控制研究[D].南京:河海大学,2008.
[6]吴长彬,燕乔.堆石料的邓肯E-B模型参数敏感性分析[J].水电能源科学,2010,28(8):94-96.
[7]尹蓉蓉,朱合华.邓肯模型参数敏感性分析[J].华东船舶工业学院学报(自然科学版),2003,17(1):19-23.
[8]刘小生,刘启旺,杨玉生.联合室内和现场试验综合确定土体本构模型参数的方法研究[R].北京:中国水利水电科学研究院,2009.

