影响GPS遥感大气水汽含量的因素分析＊

张洛恺，杨 力，李 婧，2

（1.信息工程大学，河南 郑州450001；2.61363部队，陕西 西安710054）

0 引 言

随着全球定位系统（GPS）技术的飞速发展，它的应用越来越广泛，尤其是在地球动力学、大地测量学、地球物理学、气象学、灾害预报和环境监测等领域。20世纪90年代国际上兴起了基于全球定位系统探测大气水汽含量的新技术——GPS气象学（GPS／MET），这种遥感水汽的方法具有高精度、高时空分辨率，长期稳定，不受天气影响，无需校正，费用低廉等特点，利用GPS进行大气水汽探测能很好地克服传统技术面临的问题[1－2]。

1 地基GPS反演水汽基本原理

地球中性大气对GPS信号的传播会带来路径延迟，通常的做法是将每一个测站天顶延迟作为未知数进行估算，通过干、湿映射函数投影到信号传播路径上。实际观测中，由于大气各向异性的影响，还应加入大气水平梯度，由此GPS信号传播路径上的中性大气延迟模型如下：

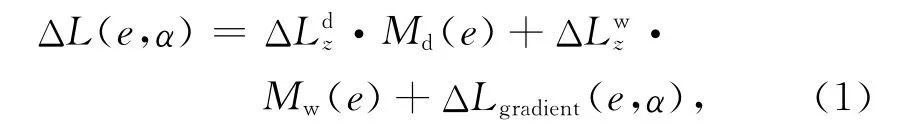
大气干项比较稳定，因此干延迟可通过测站地面的温度、气压根据经验模型估计出来，进而分离出湿延迟。国内外研究较多的经验模型有Hopfield、Saastamoinen、Black、UNB3、EGNOS和SHAO模型等[4]。获取湿延迟后，可进一步转化为与气象有关的大气可降水量（PWV），他们的关系可表示为[5]：

式中，转换因子Π是中性大气层加权平均温度的函数Tm，可取近似值0.15[6].

2 GAMIT反演水汽流程

GAMIT是由美国麻省理工学院（MIT）和美国加利福尼亚大学SCRIPPS海洋研究所研制的高精度定轨、定位GPS数据分析软件。GAMIT软件基于Fortran编写，采用双差解算方法，具有处理结果准确、运算速度快、版本更新周期短等优点，且开放源代码，因此在国内应用广泛。利用GAMIT软件解算出的天顶对流层延迟总量和可降水量精度均可达到mm量级。利用GAMIT反演大气水汽含量时可将参数设置如表1所示。

表1 GAMIT／GLOBK中部分参数设置

研究结果表明：在气象变化剧烈和低高度截止角情况下，附加水平梯度的对流层延迟模型有利于提高ZTD精度[7]。GAMIT软件中的梯度模型为

式中：C＝0.003，GE、GN分别为东西方向和南北方向的大气水平梯度；e为高度角；α为方位角。

GAMIT反演可降水量的流程主要分为表文件准备，配置文件设置、星历文件准备、测站观测数据准备、定位解算和水汽反演。GAMIT反演可降水量流程图如图1所示。

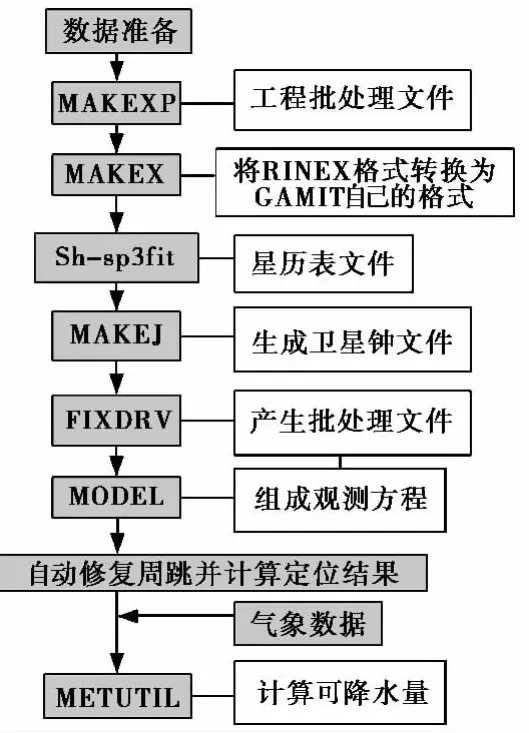
图1 GAMIT反演可降水量流程图

3 实例分析

3.1 参考站选取

地基GPS局域网中计算每个测站PWV时，先要进行定位解算，以国际GNSS服务（IGS）提供的武汉站wuhn为待测点，根据相关文献中总结的参考站选取原则[8]，选择附近均匀分布的3个全球IGS超级跟踪站上海shao、北京bjfs、昆明kunm作为参考站，如图2所示。由于相近测站对于同一颗卫星高度角几乎相等，GPS信号的传输路径和所受大气延迟量也基本相同，所以天顶方向延迟具有强相关性，这种相关性很容易在测站间求差而消除掉，使得解得的PWV值呈现出一种系统偏差[9]。解算时，为保证计算精度，其中对参考站bjfs、shao、kunm，加入长度超过500km的长基线以减小解算过程相关性，获取绝对PWV值[10]。

图2 站点分布图

3.2 解算结果精度评定

采用IGS最终精密星历，截止高度角为GAMIT默认的10°，采用13个对流层参数，计算出wuhn站在2012年第101至105天中两小时间隔的ZTD值、PWV值以及它们的中误差，由于篇幅限制只将101天的基线边解算精度如表2所示。

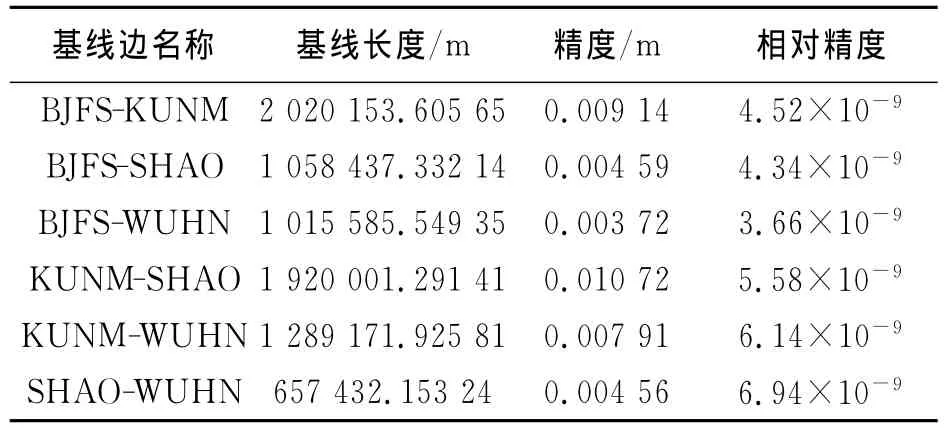
表2 基线边解算精度

该天解算的Q文件中标准化均方根误差NRMS平均值为0.16，满足一般要求的0.5[11]，基线解算的精度在10－9，满足地壳形变分析要求的10－7，这为大气水汽反演的精度奠定了基础。查看其它几天Q文件，基线解算精度同样满足要求。

根据武汉实际气象资料按照气象文件格式编写了M文件，反演了武汉站可降水量。其中ZTD中误差最大值为14.20mm，最小值为5.30mm，平均值为7.90mm，PWV的中误差最大值为1.97 mm，最小值为0.85mm，平均值为1.27mm，解算的精度较高。将GAMIT的ZTD结果与IGS机构下的CODE中心提供的参考值比较，最大偏差达到15.80mm，平均偏差为2.33mm，标准差为5.28mm。这是由于GAMIT软件计算ZTD值采用精确线性模型（plecewisehnear），计算得到的结果相对平滑，但离散性较差[12]。探空值获取时刻为12点和0点，将解算结果与IGRA提供的探空值分别求差，最大值为10.86mm，平均值为2.03 mm，标准差为3.58mm.另外计算时没有采用适合当地的大气加权平均温度模型，而是采用GAMIT默认设置，这对反演精度也会产生影响。

3.3 对流层参数个数设置

在GAMIT配置文件sestbl.中可设置对流层延迟参数的个数，一般可取13、25、49，分别对应的时间分辨率为2h，1h，0.5h。现采用事后精密星历，截止高度角设为10°，将不同对流层参数解算的ZTD与IGS提供的参考值进行对比，如图3所示。可以看出它们的趋势与IGS提供的参考值一致，分别将13参数、25参数、49参数ZTD值与IGS参考值的作差，差值非常接近，最大值依次为15.80mm、17.60mm、19.40mm，较差平均值依次为2.33mm、0.12mm、0.93mm，标准差依次为5.28mm、6.87mm、7.13mm.图4示出了不同对流层参数解算PWV值对比，三条曲线走势一致，两两之间差值最大不超过1mm.由于大气水汽增量与降水量关系密切[2]，三种方案的解算结果与武汉2012年4月10日的降雨实情相符，在大气水汽总量迅速增加后的6～7h，即当天14点至15点，降雨量达到了8mm，可见三种方案在中小尺度天气预报中都能起到灾前提醒和预防的作用。

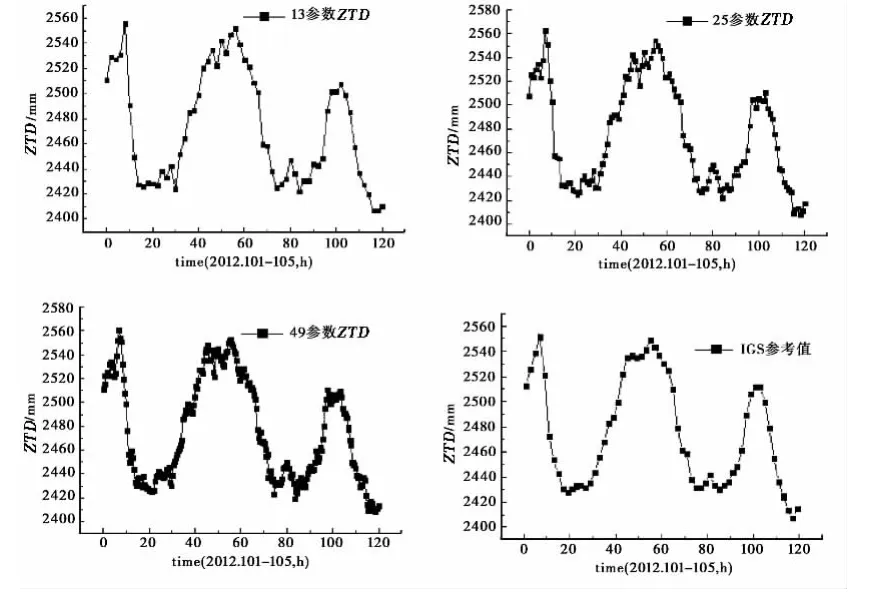
图3 不同对流层参数解算天顶延迟量对比

图4 不同对流层参数解算PWV值对比

实际应用中，在精度符合要求的情况下我们往往要求提供的信息能更及时，从而对灾害事件的把握和防范就更充分，天气预报一般需要在半小时甚至更短的时间内提供新的信息，故0.5h的时间分辨率也更满足实际应用的需要。

3.4 卫星星历精度对PWV的影响

实验分别利用IGS提供的超快星历IGU的预报部分和实测部分、快速星历IGR、事后星历IGS对whun站可降水量进行解算，对流层参数个数设为25，截止高度角10°.星历相关信息如表3所示，不同星历解算天顶延迟量对比如图5所示。

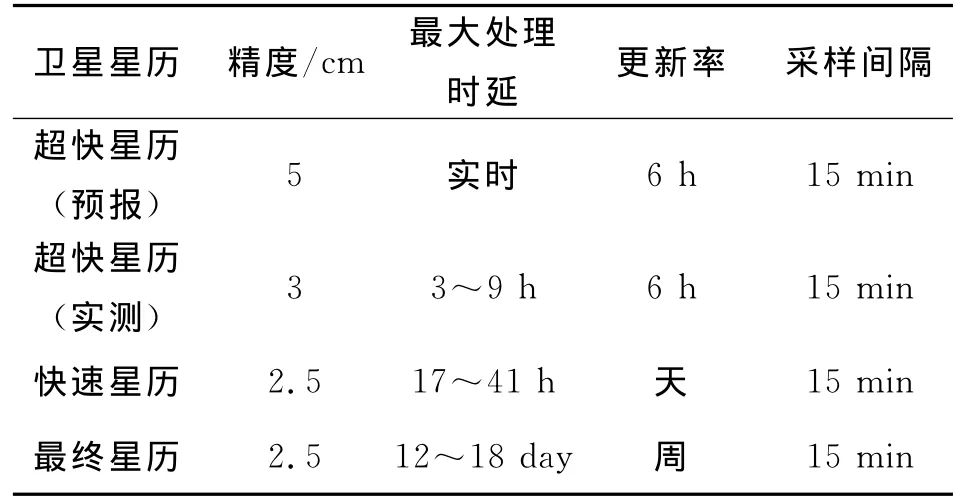
表3 卫星星历及其精度

图5 不同星历解算天顶延迟量对比

图6 不同星历解算PWV值对比

将ZTD结果与IGS参考值比较，超快星历预报部分得到的平均偏差0.89mm大于实测部分的0.31mm，快速星历的0.27mm和最终星历的0.12mm.超快星历预报、超快星历实测、快速星历、最终星历与参考值较差的标准差很接近，依次为6.94mm、6.84mm、6.91mm 和6.87mm.图6示出了不同星历解算的PWV值，快速星历和最终星历反演结果几乎相等，超快速星历解算的PWV值与它们相差仅在1mm以内，由此可见，超快速星历预报部分引起的误差是可以接受的。

3.5 截止高度角设置

卫星高度角的变化影响着卫星的空间几何分布，从而影响对测站的坐标、对流层延迟量等的解算精算，通过设置高度角还可以减小多路径效应的影响。图7示出了所有观测站高度角统一设置5°、10°、15°、20°和25°时的ZTD 值，通过对比发现，当高度角取15°时解算结果与IGS提供ZTD的参考值符合最好，5°到25°的标准差（mm）依次为：6.87、6.87、6.37、7.07、8.53.对 比PWV 值 和IGRA 探空值发现高度角大于20°时，GPS遥感水汽值偏差较大，20°以下相差则较小，如图8所示，因此不建议采用截止高度角大于20°。

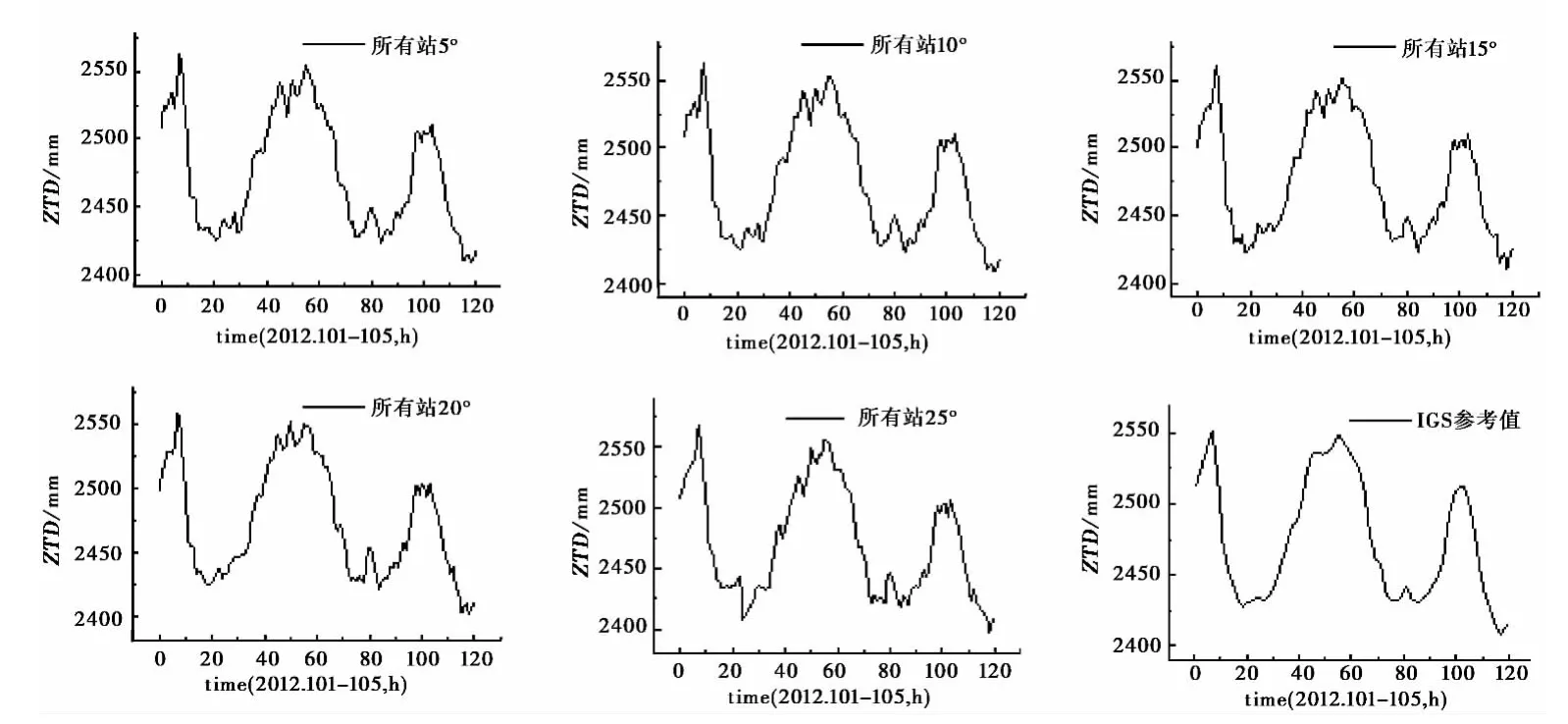
图7 所有站设置某高度角时的天顶延迟量

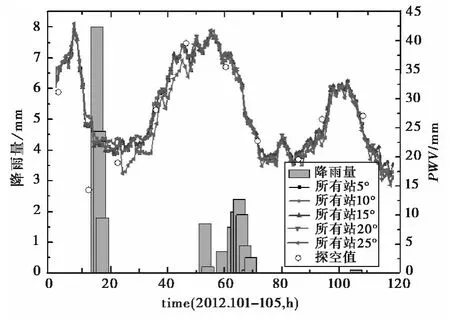
图8 所有站设置某高度角时PWV值

为进一步验证，将待测站wuhn的高度角设置为5°到25°不等，其他测站均设置15°，计算出PWV值并与探空值比较，所得结论同上，即当所有测站高度角设置为15°时精度最佳。图9示出了设置不同高度角时与探空值比较得到的标准差。

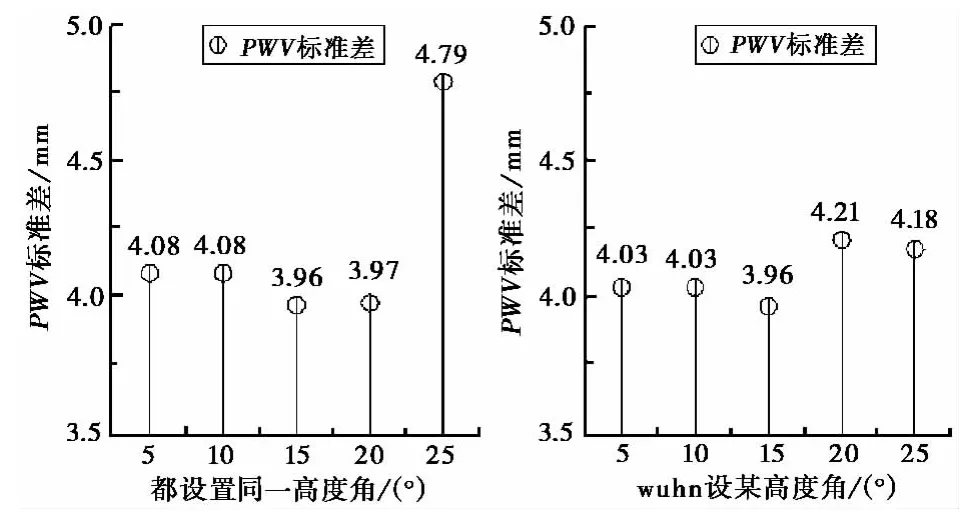
图9 不同高度角PWV值标准差

4 结 论

文中列出了利用GAMIT计算大气水汽含量时的一些常用参数设置和计算的注意事项，如考虑控制站几何布局，以及加入大于500km的控制站以减小解算过程的相关性等。GAMIT基线解算精度的保证，为大气水汽的反演奠定了基础，同时实验结果与IGS提供的天顶对流层延迟量吻合良好，实验解算PWV的中误差在1mm左右。

通过设置不同天顶对流层延迟参数个数，解算不同时间分辨率的可降水量，它们相差在1mm以内。因此在精度满足要求的情况下，往往选择半小时甚至15min提供一次信息，故将对流层参数设为49也更满足实际应用的需要。星历精度对水汽含量的计算也有一定影响，但目前IGS提供的超快速星历、快速星历、事后星历计算出PWV相差都在1mm以内，因此采用超快速星历能够满足实时水汽监测的要求。研究了截止高度角对GPS反演可降水量的影响，实验发现将截止高度角设为15°时遥感大气水汽含量的精度最高。

致谢：感谢美国 MIT授权使用GAMIT／GLOBK软件，感谢湖北气象局提供武汉市气象和降雨量数据。

[1]BEVIS M，BUSINGER S，HERRING T A，et al.GPS meteorology：remote sensing of atmospheric water vaporusing the global positioning system [J].Geophys.Res.，1992，97（D14）：15787－15801.

[2]曹云昌，方宗义，夏 青.地基GPS气象站网建设指南[M].北京：气象出版社，2007.

[3]宋淑丽，朱文耀，廖新浩.地基GPS气象学研究的主要问题及最新进展[J].地球科学进展，2004，19（2）：250－259.

[4]曲伟菁，朱文耀，宋淑丽，等.三种对流层延迟改正模型精度评估[J].天文学报，2008，49（1）：124.

[5]曲建光.GPS遥感气象要素的理论与应用研究[D].武汉：武汉大学，2005.

[6]HAASEet al.ZTD water vapor in the western mediterranean submitted to bull[J].Am Meteor Soc.，2002（3）：9－10.

[7]李 黎，匡翠林，朱建军，等.水平梯度和映射函数对PPP对流层延迟估计的影响分析[J].工程勘测，2011（5）：228.

[8]隋立芬，许其凤.GPS数据处理中IGS基准站的选取[J].测绘学院学报，2003，20（1）：1－3.

[9]郭志梅，李 黄，缪启龙.GPS探测气象参数的技术进展[J].气候与环境研究，2008：96－106.

[10]DUAN J，BEVIS M，FANG P，et al.GPS meteorology：directestimation of the absolute value of precipitable water vapor[J].J.Appl.Meteor.，1996（35）：830－838.

[11]王 皓，李国平，陈娇娜.运用GAMIT10.34解算成都地区的GPS可降水量[J].成都信息工程学院学报，2009，24（5）：458.

[12]王京丽，张朝林，楚艳丽，等.利用Berne GPS软件解算地基GPS大气可降水量的研究[C]／／新世纪气象科技创新与大气科学发展——中国气象学会2003年年会“城市气象与科技奥运”分会论文集，2003.