基于相对极差转换的小批量生产过程质量控制研究
曾 文 卿艳梅 夏红梅 张殿武
(华南农业大学 工程学院,广东 广州 510642)
0 引 言
传统的质量控制理论是建立在经典统计理论上的,主要适用于大批量生产、样本量大的情况。但现代加工制造业50%以上属于多品种、小批量生产,同时由于柔性化制造、敏捷制造等先进生产技术的大力推广,多品种、小批量生产将更加普遍。在这类多品种、小批量生产环境下,采用传统休哈特控制图控制这类生产过程的质量特性时,样本量无法满足休哈特控制图大数据量的要求。为实现对多品种、小批量生产过程的质量控制,国内外进行了大量的研究。主要存在以下几种方法:一是通过精确调整控制图控制界限,使每个点的第Ⅰ类错误概率最小。King[1]、Hiller.F.S[2]、Del.Castillo[3]等做了大量的研究,这种方法在小样本数据量时精确控制限的统计过程质量控制方法是有效的,但精确控制限法由于其控制限随样本容量的变化而异,不利于发现第 II类错误;二是基于贝叶斯预测,将历史检验数据与人们的主观评价、预测和判断相结合,通过综合主、客观信息来建立过程的动态模型,对过程变化作出预测,从而在保证预测精度的同时,大大减少了对样本容量的要求,Harrison.P.J.[4]、卜祥民[5]、林忠钦[6]等在此方面进行了大量的研究工作,但由于人们对过程的主观评价难以预测正确,影响了其在实际中的有效应用;三是通过将相似工序的质量特性数据进行数学变换成同分布的数据,以扩大数据量实现在传统休哈特控制图中进行控制。Quesenberry.C.P.[7]、余忠华[8]、刘春雷[9]、范文贵[10]等在这方面进行了大量的研究工作。这种方法需要对相似工序进行分组,因此对质量工程师的要求相对较高。
本文针对相似工序的质量特性,提出了一种相对极差转换的方法,扩大样本数据量,实现利用休哈特控制图控制生产过程的稳定性,以解决多品种、小批量生产过程的质量控制问题。
1 相对极差转换法的质量控制研究
1.1相对极差转换法的原理分析
设质量特性 X 数据 x1, x2, …, xn,服从正态分布 N(μ, σ2)。其数据的模型可描述为:

式中:xi为特性的实际测量值;μ为数据的均值;εi为数据的随机误差,εi服从正态分布N(0, σ2)。
相对极差转换公式为:

数据模型(1)经相对极差转换公式(2)变换后质量特性数据变为y1, y2, …, yn,其数据模型可描述为:


经相对极差变换后的质量特性均值和标准差分别为:
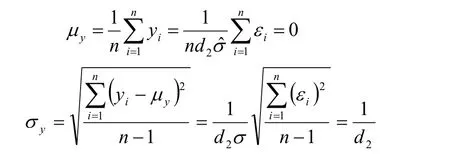
因此经数据变换后,转换后的质量特性数据符合正态分布 N(0, (1/d2)2)。对于多个相似工序质量特性,当每个质量特性子组样本容量一致时 d2的取值相同,经此公式进行数据变换后,转换后的数据均符合正态分布N(0, (1/d2)2)。 因此,可以将多个相似工序质量特性的数据作为一个整体,应用传统休哈特控制图进行质量控制,从而解决小批量生产条件下单个质量特性数据量不足的问题。
1.2质量控制图控制限分析
由相对极差转换法的原理可知,转换后的数据服从N(0,(1/d2)2)正态分布,即均值μ=0,标准差σ=1/d2。对于Xbar-R控制图而言,因 μR=d2σ=1,σR=d3σ=d3/d2,因此有:
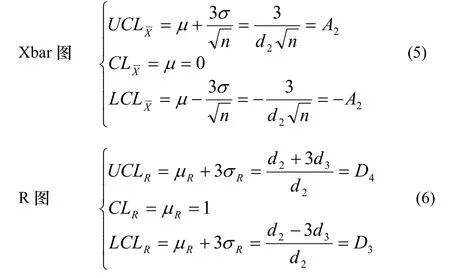
式中A2与D4的值取决于子组样本的数量n,即当子组样本容量n一定时,采用相对极差转换法的Xbar-R控制图为固定值。
对于IX-MR单值移动极差控制图,因多品种小批量生产过程的采样数据本身较少,所以其移动数n取2比较合适。当 n 取 2 时,d2=1.128,d3=0.853,μR=d2σ=1,σR=d3σ=d3/d2=0.7562,因此有:
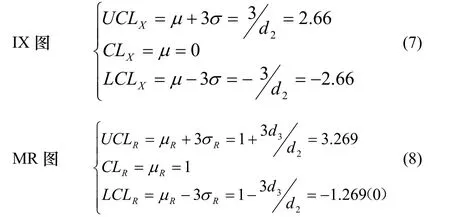
对于Xbar-S均值标准差控制图而言,因多品种小批量的数据本身较少,无法满足Xbar-S控制图要求子组样本容量大于10的要求,所以Xbar-S图不适合于多品种小批量的质量控制。
1.3 相对极差转换法的特点分析
从相对极差转换法的原理及其质量控制图控制限的分析中可以得出以下特点:
(1) 相对极差转换法可以将多个相似工序的具有不同尺寸值、公差范围和标准差的质量特性结合在一张控制图上,以控制过程的稳定性。
(2) 如果采用 Xbar-R图进行控制,则多个质量特性的数据分组的样本容量n必须一致,以保证参数d3,d2相同。如果采用IX-MR图进行控制,则所有质量特性的移动数n取2。
(3) 需要估计每个质量特性的均值目标值和极差目标值。因此每个质量特性的数据量不宜太少。一般来说,采用Xbar-R控制图,每个质量特性的子组数要大于2以上,采用IX-MR控制图,则每个质量特性的数据量要大于3个以上。
(4) Xbar-R控制图和IX-MR控制图的控制限都是固定值,不会随着数据的变化产生变化,利于观察过程的稳定性。
从相对极差转换的特点看,在多品种、小批量生产过程中,比较适合采用相对极差转换的方法对多个相似工序的质量特性进行控制,以保证生产过程的稳定性。
2 案例分析
某汽车配件厂中,有5种不同规格的轴类零件在同一数控车床中加工,各零件的基本尺寸、公差均不相同,其规格如表1所示。获得的样本测量数据如表2所示。
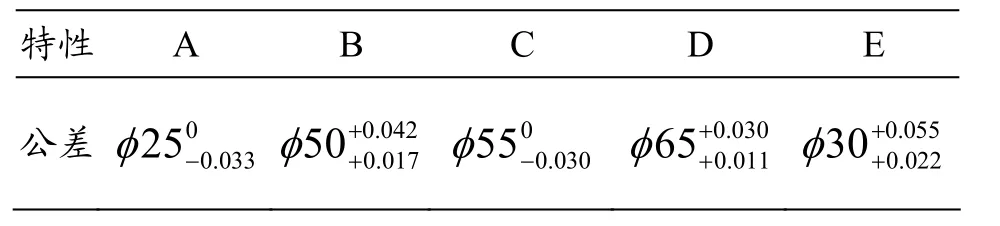
表1. 各种零件的公差
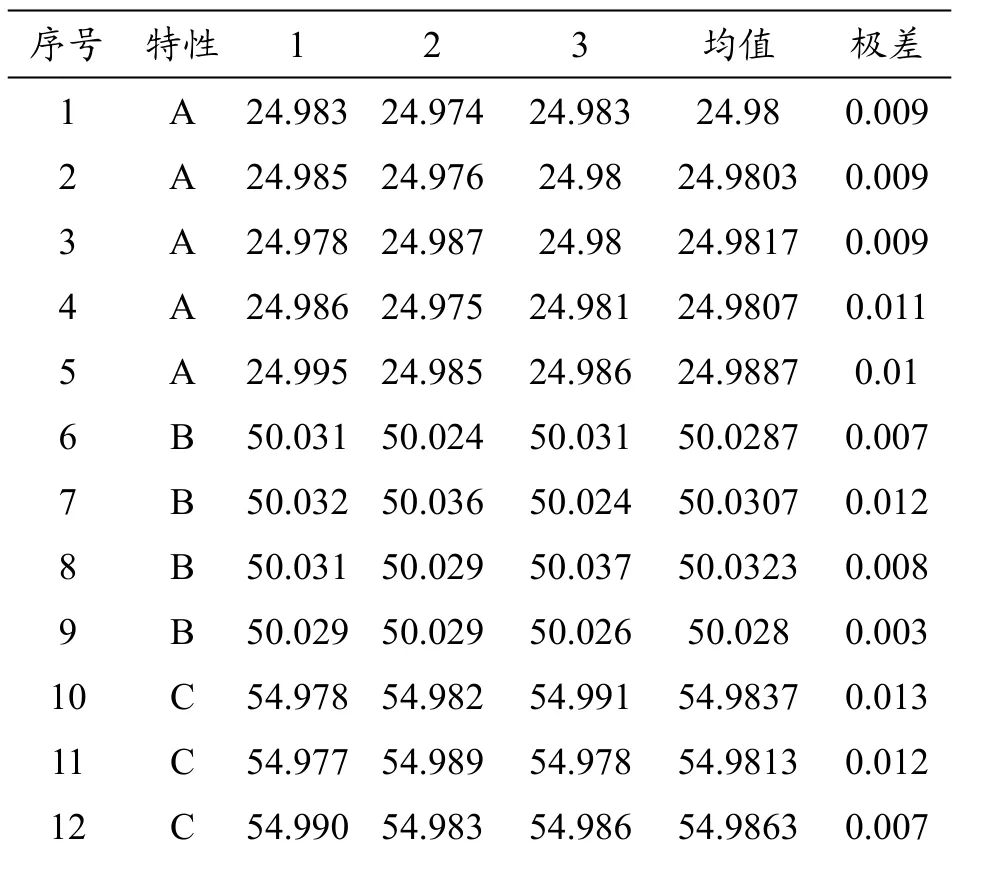
表2. 样本测量数据
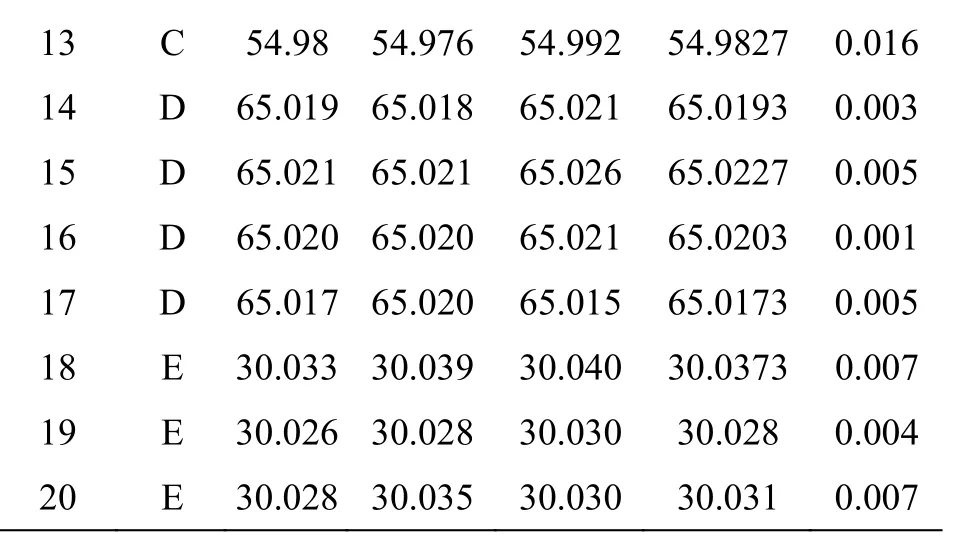
13 C 54.98 54.976 54.992 54.9827 0.016 14 D 65.019 65.018 65.021 65.0193 0.003 15 D 65.021 65.021 65.026 65.0227 0.005 16 D 65.020 65.020 65.021 65.0203 0.001 17 D 65.017 65.020 65.015 65.0173 0.005 18 E 30.033 30.039 30.040 30.0373 0.007 19 E 30.026 30.028 30.030 30.028 0.004 20 E 30.028 30.035 30.030 30.031 0.007
首先利用原始样本测量数据计算各质量特性的均值与极差估计值,如表3所示。

表3. 各质量特性的均值与极差估计值
然后利用相对极差转换公式(2)对表2中数据进行转换,并计算Xbar和R图的控制限,由于子组样本容量n=3,所以A2取值为1.023,D4取值为2.573,D3取值为0,故Xbar-R图控制限如下:

最后,利用转换后的数据及其控制限制作Xbar-R控制图如图1所示。稳定受控状态。
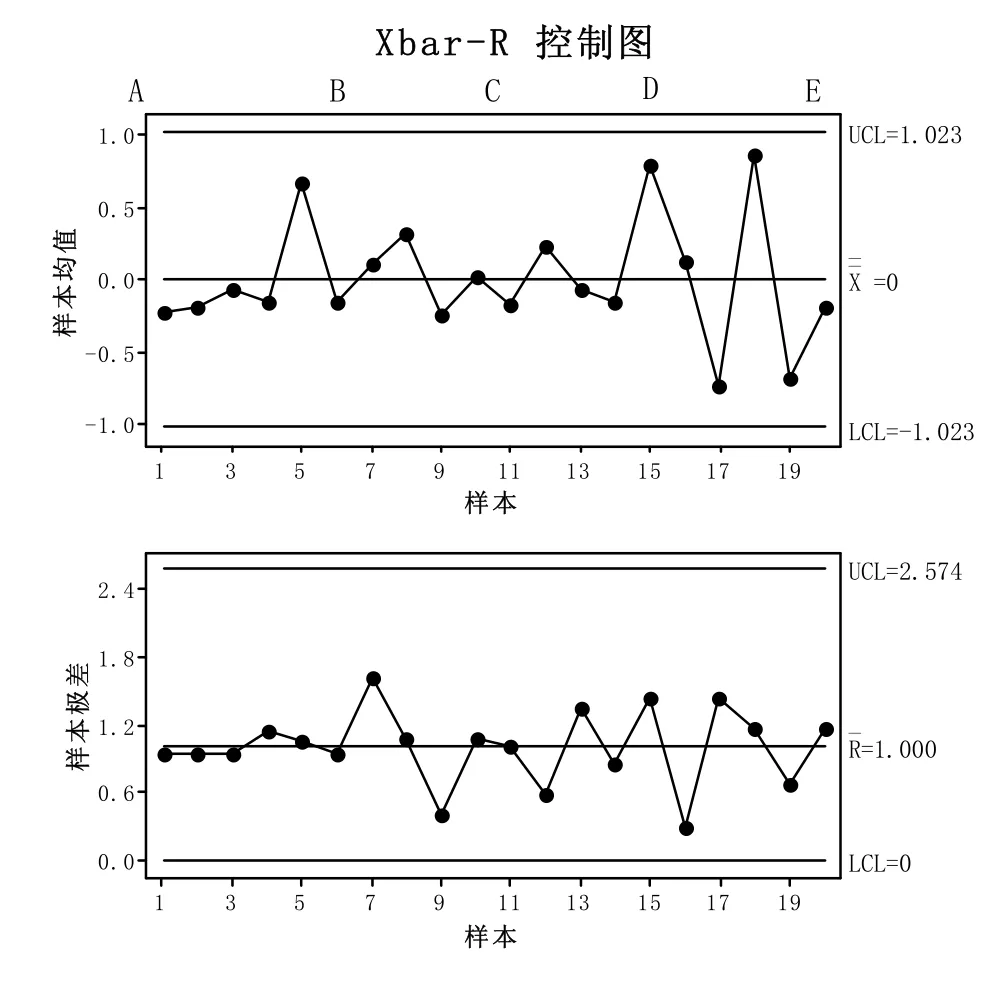
图1. 相对极差转换法的Xbar-R控制图
3 结 论
小批量生产将逐渐成为 21世纪制造业的主要生产方式,对小批量生产过程的质量控制也日益显得更加重要。本文提出的基于相对极差变换的数据变换方法有利于实现多个相似工序质量特性的小批量过程质量控制,具有固定控制限、对质量特性的尺寸值、公差大小、标准差无一致性要求、均值及极差估计简单、控制图制作方便等特点,既适用于均值极差控制,也适用于单值移动极差控制,对于实现多品种小批量生产过程的质量控制有比较广泛的适用性。
[1]King.E.P. Probability Limits for the Average Chart When Process Standards Are Unspecified[J]. Industrial Quality Control. 1954, 10 (6): 62-64.
[2]F.S.Hillier. X and R Chart Control Limits Based on a Small Number Subgroups[J]. Journal of Quality Technology. 1969,(1): 17-26.
[3]Del. Castillo, Montgomery. D. C. Short Run Statistical Process Control:Q-Chart Enhancements and Alternative Methods[J]. Quality and Reliability Engineering International.1996, (10): 87- 97.
[4]张孝令等. 贝叶斯动态模型及其预测[M],济南:山东科学技术出版社,1992.
[5]卜祥民. 小批量质量控制与诊断[D]. 北京航空航天大学博士学位论文, 1998.
[6]林忠钦, 连军, 倪军, 来新民, 陈关龙. 基于小样本的车身装配尺寸质量动态高精度评价方法[J]. 机械工程学报.2001, 37 (11): 62-65.
[7]Quesenberry. Charles. P. SPC Q Chart for Start-Up Processes and Short or Long Runs[J]. Journal of Quality Technology. 1991, 23(3): 213-224.
[8]余忠华, 吴昭同. 面向小批量制造过程的质量控制方法研究[J]. 机械工程学报, 2001, 37(8):60-64.
[9]刘春雷, 王慧, 付秀丽, 解德凤. 多品种小批量生产模式下质量控制数据转换方法研究[J]. 组合机床与自动化加工技术, 2009, 4: 34-36.
[10]范文贵, 李林, 钱明. 面向多品种小批量生产的 SPC 研究[J]. 制造业自动化, 2009, 31(9):61-64.

