思维要“逼”，探究才能进行到底——由一堂《二元一次方程组的图像解法》的公开课说起

☉浙江省绍兴县稽东镇中学 尉嗣侃

思维要“逼”，探究才能进行到底
——由一堂《二元一次方程组的图像解法》的公开课说起

☉浙江省绍兴县稽东镇中学 尉嗣侃

“数学是思维的体操”，可以锻炼学生的思维能力，使其不断地发展.《新课标》中明确指出数学在应用方面需要大力加强，鼓励学生发现数学的规律和问题解决的途径，使他们经历知识的形成过程.当今的数学课堂呈现出一种探究式教学的模式，但何为探究，如何探究，却引人深思！

部分数学课堂常常让学生讨论、交流，或者动手画一画、量一量、折一折，教师便问学生有何发现，看似探究味儿十足，但学生其实是被动式的接受知识，数学的思维也未得到任何发展，并不能发现知识的规律和本质.笔者认为学生的思维在一定程度上不得不“逼”，一些简单的问题或直观的结论学生往往是凭借记忆或感觉而得出的，并不能领悟问题的实质，所以教师要在教学的过程中不停的追问，不停的让学生感觉难以回答，于是学生才会积极在头脑中搜索知识，这样思维碰撞后才能“逼”出他们最深层的思想，才能将探究进行到底.

笔者就以曾上过的一节公开课《二元一次方程组的图像解法》的4个片段入手与读者交流，共同体会从课堂的点滴出发，“逼”出学生的思想，真正让课堂充满探究的意味儿.

一、问题情境

师：前面的课中我们学习了一次函数图像的画法，下面请同学们在平面直角坐标系中，画出一次函数y=－x+3的图像，并在直线上标出任意3个点，写出相对应的坐标.

（学生动笔在学案上画图像，并写出坐标，教师巡视时提醒学生记得在图像旁标明函数的解析式）

生：我找的三个点的坐标为（ 0，3）、（ 1，2）、（ 3，0）.

师：请你将三个点的坐标换一种语言转换成我们熟悉的形式，比如（ 0，3）可以转换成当x=0时，y=3.

生：（ 1，2）、（ 3，0）分别可以转换成当x=1时，y=2；当x=3时，y=0.

师：继续换个角度来研究，式子y=－x+3其实大家十分熟悉，虽然它现在是一次函数，但我们对它早就了解，以前它叫什么？

生：二元一次方程.

师：那么当x=0时，y=3满足于二元一次方程y=－x+3吗？ 当x=1时，y=2呢？ 当x=3时，y=0呢？

生：均满足.

师：对于不同的式子说不同的话，既然满足于方程，那我们要写成怎样的形式？

师：直线y=－x+3上有多少个点？不会大家找的都是这三个点吧？有不同的点吗？

（学生积极举手，说出自己所找的点的坐标）

师：这些点写成解的形式是方程y=－x+3的解吗？

生：是的！

师：如果再找第4个、第5个点呢？你有什么发现？

分析：通过不停的追问，让学生感受从特殊到一般的过程，让学生的思维不断完善，便很容易的归纳出：一次函数图像上任意一点的坐标都是对应的二元一次方程的一组解.

二、建构活动

1.方程的解与函数的点的坐标对应

师：下面给同学们一个机会，写出方程y=－x+3的任意3组解，并把这些解写成点的坐标形式，并在平面直角坐标系内标出这些点.

（学生动手操作，并在平面直角坐标系内标出）

师：你发现这些点在哪儿？

生：点在直线上.

师：直线有很多条，到底在什么直线上？

生：直线y=－x+3上.

师：那如果我再找几个解，写成点的坐标形式，你觉得这些点还在这条直线上吗？

生：是的！

师：老师突然感觉十分激动，以前二元一次方程的解是一组数，现在却能看得见了，你有这样的感觉吗？你又有什么发现呢？

生：二元一次方程组的解在直线上.

师：这说法不对，解怎么可能在直线上？

生：那解写成坐标在直线上！

师：坐标也不会在直线上呀？

（学生此时难以描述，有很多话想说但不知道如何组织语言，思考了几秒钟以后，回答出：以二元一次方程的解为坐标的点都在对应的一次函数的图像上）

师：你能用一句通俗易懂的话来总结上面两个发现吗？

分析：这次的追问“逼”出了学生的思想，真正明白了对于不同的式子说不同的话，要注意语言的规范.学生在仔细思考后，组织了语言：二元一次方程的解与相对应的一次函数的图像上的点的坐标一一对应.笔者迅速将其在黑板上记录，上述一系列的“逼”，使学生的思维更上了一层，明白了点的坐标和方程的解对应、方程与函数的式子对应的双重关系，这是学生的第一次思维被完整“逼”出.

2.二元一次方程组的解与函数图像的交点的坐标对应

师：请再画出y=x－5的图像，为了节省纸张，我们画在同一个平面直角坐标系内（也为后面的活动埋下伏笔）.

（学生画好后，仿照之前的发现叙述一次对应关系）

师：既然y=x－5与y=－x+3的图像在同一平面直角坐标系中，那我们就来研究一下，这两条相交直线上有无数个点，老师觉得有一点很值得研究，你觉得呢？

生：交点很有研究价值.

师：价值在哪儿？

生：它是对应的方程组的解.

师：交点会是一个方程组的解吗？交点不就是一个点吗？

生（有些着急）：讲错了，是交点的坐标.

师：那为什么是呢？

生：因为交点既在y=x－5的图像上，又在y=－x+3的图像上，所以这个点是公共点，按照我们之前的发现，公共点的坐标对应公共解，也就是说这个点的坐标既符合方程y=x－5，又符合方程y=－x+3，也就是公共解，两个方程的公共解就是方程组的解，所以这个交点的坐标就是对应的方程组的解.

（这次的追问让学生说出了自己的完整想法，也让结论更加清晰）

师：难道同一平面直角坐标系中，两条直线一定有一个交点吗？

分析：不停的“逼”，让学生的思维主动“跳”了出来，对知识更加明确，于是回答：如果两个一次函数的图像有一个交点，即两直线相交，那么二元一次方程组有唯一解，交点的坐标就是相对应的二元一次方程组的解；如果两个一次函数的图像有无数个交点，即两直线重合，那么相对应的二元一次方程组有无数组解；如果两个一次函数的图像没有交点，即两直线平行，那么相对应的二元一次方程组无解.学生的这个回答比书本上的结论还要完整，也充分体现了数学结论是在不断完善中形成的，笔者给予学生高度的赞赏，第二次的“逼”达到了完美的效果.

（笔者立马出了几个训练题强化二元一次方程组的解与交点坐标对应的题）

三、数学化认识

师：看到这个二元一次方程组，你有什么想法？

生：除了可以利用加减消元法、代入消元法，还可以利用找交点的方法来解.

师：那你会怎么找交点来解呢？要经历哪些步骤？

生：首先把方程形式转换成函数形式，接着在同一平面直角坐标系内画图像并找到交点，最后转换成解的形式.

师：很好，可以简记为变函数、画图像、找交点、写结论.

分析：这次的“逼”让学生多了一种方法来解决二元一次方程组的解，并了解这种图像解法的步骤，虽然学生体会到方程和函数之间的联系，但并不了解为何要学习这节课，用意何在，为何要将一个简单的题目复杂化.

（笔者针对这类题给予了一个例题，并板书格式、步骤）

四、能力拓展

1.以图看解

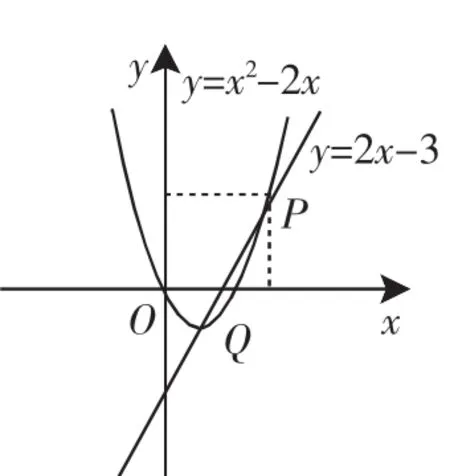
图1

师：你能解释一下吗？

生：通过上面的发现知道交点的坐标就是方程组的解.

师：我们上面讲的是二元一次方程组的图像解法，而这个图像所表示的好像不是一次函数吧？那你又有什么发现呢？

生：如果两个图像有交点，那么交点的坐标就是对应的方程组的解，我们可以扩展为通过交点来求二元高次方程组的解了.

分析：这个“逼”让学生逐渐意识到图像解法是一个通法，“逼”学生说出可以用其解决二元高次方程组的解，但有的学生依然会用以前的方法解决本题，而有些学生已经逐步意识到图像解法也是应该掌握的一个方法了.

2.以题作图

（学生知道这节课在学图像解法，但是仍然喜欢用自己原先学过的消元法，因为学生觉得消元法更简单、更熟悉、更方便，于是将这个方程组消去y，得到含有x的方程：x5－x－1=0，看到这个方程，学生们彻底放弃，因为他们根本不会解，这正是笔者想要的结果，为笔者的下一个“逼”提供了帮助）

师：我相信大家肯定尝试了原来的方法，你会解吗？其实老师也不会，那我们该怎么办呢？

生：用图像法试试吧！

师：对于消元法，虽然有时候很简单，但遇到不会解的方程你就无从下手了，而图像人人都会画，多找一些点图像就会更精确，那我们用图像法试试看.

（为了节省时间，笔者用几何画板展示了两个函数的图像，并清晰的找到了交点，虽然交点的坐标是近似数，但方法显然是可行的）

分析：通过这次的“逼”，让学生无计可施，终于在此时感受到今天的学习是有价值的，图像解法也是一种学习过程中必不可少的方法.

（学生想都不想，看到五次方马上开始动手画图像）

师：有人发现了什么吗？

生：画图像来解决此题！

师：一定要画图像吗？你用以前的方法看看.

（学生将这个方程组消去y，得到含有x的方程：x5=x，看到这个方程恍然大悟，很快解出了方程组，觉得又被老师欺骗了）

为了让学生得到更加清晰的结果，笔者用几何画板展示了图像并找到了交点，直观的几何画板展示让学生发现用图像和消元法的结果是一样的.

分析：通过这次的“逼”，学生清晰地意识到图像解法是正确的方法，在遇到不会求解的二元高次方程组的时候利用图像解法能体现其优势，真正的学以致用，明白选对方法很重要.

上面几个片段中，虽然没有一处让学生开展讨论，但是处处渗透探究，从一节课的开始到一节课的结束都以问题为核心，不停根据学生的回答继而追问，用一个又一个的问题“逼”学生展示自己，“逼”学生说出自己的最真实想法，不断地使学生的知识内化，转为生成经验，也“逼”出了本节课的规律.所以无论何时，数学课堂不得不“逼”，这样才能探数学之实质，究数学之本质，让探究进行到底！