双渠道回收下闭环供应链的定价与协调策略

张成堂，杨善林

（1.安徽农业大学 理学院，安徽 合肥 230036；2.合肥工业大学 管理学院，安徽 合肥 230009）

0 引言

随着全球资源的日益短缺和人们环保意识的不断加强，很多国家纷纷加大了环境与资源保护立法的力度［1］，废旧产品的回收再制造已引起业界的广泛关注［2－4］。许多企业如惠普、柯达等发现，废旧产品的回收利用可以大幅度节省制造成本，提高企业的社会声誉和经济效益，从而开创了“资源—生产—消费—再生资源”的闭环反馈式循环供应链［5］。该循环过程减少了对初始资源的获取和最终垃圾的数量，有助于制造企业实现经济与环境的协调发展，对整个社会的可持续发展具有积极的意义。

在闭环供应链管理中，产品回收与销售的定价决策非常关键，它直接影响到产品的供需状况和闭环供应链的运作效率。因此，近年来闭环供应链的定价问题成为学界关注的重要议题，文献［6］研究了闭环供应链中不同回收结构的定价策略和渠道效率问题，但其研究假定废旧品的回收量是成品市场需求量的一个比例，没有考虑回收价格对废旧品回收量的影响，把废旧品的回收价格看成是外生变量，这与现实情形不符；文献［7］采用期货定价模型，研究了集中式决策下，产品销售价服从几何布朗运动时制造商需要面临的回收产品定价问题；文献［8］运用博弈论和模糊理论研究了零售商竞争下闭环供应链的最优批发价和零售价；文献［9］则在新产品与再制造品售价相同、需求与价格相关情形下，考察了两类产品的生产数量、售价和废旧品回收价格，但实际市场上再制造品的价格往往与新产品不同，需求也不尽相同。

关于闭环供应链协调定价方面的研究相对较少，文献［10］在随机需求下研究了零售商负责分销和回收的闭环供应链，分析了闭环供应链节点企业的定价决策问题，并提出一个收入－费用共享契约，实现了单渠道回收下闭环供应链系统的协调；文献［11］运用博弈理论分析了混合回收对节点企业定价决策和利润的影响，并利用两部定价契约改善了成员企业和整个闭环链的绩效，不过制造商作为渠道的领导者，将索取合作后的全部超额利润，零售商只能获得分散化决策下的利润。另外，闭环供应链的研究还有关于不同回收渠道和模式［12－13］、不同回收效率［14－15］下的定价策略和系统绩效问题，很少涉及多个渠道同时回收以及渠道冲突性的研究。

目前，国内外学者对闭环供应链定价策略及协调问题的研究取得了一些成果，但仍存在明显不足：①多数研究以简单的线性需求量和线性回收量为假设，这与现实生活中对各种产品的需求呈现为非线性形态不相符，且回收价格、回收量往往与回收渠道显著相关；②由于消费者的感受和认知等原因，对新产品和再制造品的认可程度和需求会存在差异，而多数研究均假设两种产品以相同价格出售，实际上再制造品售价一般比新产品低；③大部分研究对回收再制造产品的利润都以获取再制造节省的成本来结算，没有涉及再制造品的销售利润，有的研究直接假设再制造产品全部能够销售出去而获取利润，而实际情形中再制造品的需求一般都远低于新产品的需求，因此再制造品会有部分剩余；④对于闭环供应链的协调定价研究，如果是在双渠道回收模式下，仅采用收入－费用共享契约并不能达到协调的目的，而文献［11］采用的两部定价契约也很难让零售商有响应的积极性，缺乏可操作性。

依据上述分析，本文将基于新产品和再制造品的差异化销售、两种产品的市场需求为价格敏感型、废旧品回收量与回收渠道冲突有关、剩余再制造品有残值收益等假设，建立双渠道回收模式下闭环供应链系统的定价与协调模型，主要分析以下几个问题：①比较Stackelberg博弈定价和联合决策定价模式下，各节点企业的产品销售与回收价格、供应链系统的绩效等；②仅采用收入－费用共享契约不能协调该闭环供应链的原因，如果与两部收费制相结合，那么所构成的组合协调定价模式能否完美协调该系统；③在新产品和再制造产品的弹性需求市场，二者是否有“挤兑效应”，对系统绩效有何影响；④成本参数、渠道冲突等对三种定价模型下均衡结果的影响。

1 模型假设与符号约定

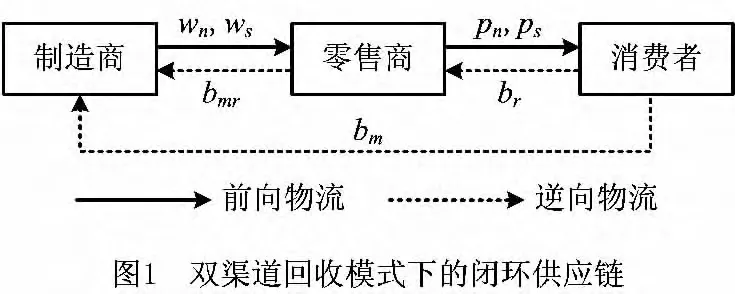
本文主要考察一个由制造商和零售商组成的单周期闭环供应链系统，该供应链系统上的制造商直接向消费者回收废旧产品和间接通过零售商回收产品，然后利用回收品进行产品再制造。现实中存在很多类似情形，特别是汽车、电子类等产品，厂家有的采取直接回收方式，有的间接通过销售企业进行回收。再制造品和新产品在功能上无明显差异，仅在价格和认可程度上存在差异，新产品和再制造品在销售时实行差别定价，遵照循环经济法，再制造品均有显著标志。

文中使用到的相关符号约定如下：

cn，cs分别为制造商新产品、再制造品的边际生产成本；

wn，ws分别为制造商新产品、再制造品的批发价格；

pn，ps分别为零售商新产品、再制造品的零售价格；

br为零售商的废品回收价格；

bm为制造商的废品直接回收价格；

bmr为制造商的废品间接回收价格。

这里，wn，ws，bm和bmr是制造商的决策变量，pn，ps和br是零售商的决策变量。

相关假设如下：

（1）该类产品在市场上发展成熟，事先有可回收的废旧产品，并且回收的废旧产品全部进行再制造，再制造率为1。

（2）假设当前市场对新产品和再制造品的需求为售价pn，ps的非线性减函数：

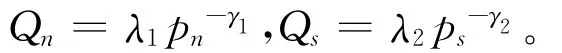
式中：λ1和λ2为常数，λ1，λ2＞0；γ1和γ2分别为新产品、再制造品的市场需求对其销售价格的敏感系数，γ1，γ2＞1。

（3）因为消费者对再制造品的认知度不高，导致再制造品的市场需求相对较低，所以可假设再制造品的数量供大于求，对于“未能售出的再制造品”，制造商获得一定的残值v，且v＞cs＋bm，v＞cs＋bmr，以保证制造商有回收再制造的动力。另外，要求v＜ws＜ps，以保证制造商积极销售再制造品。

（4）在双渠道回收模式下，假定bm＞br。因为零售商最接近市场终端，加之消费者会更倾向于零售商回收的便捷性，所以只有当制造商支付的回收价格高于零售商所支付的回收价格时，制造商的直接回收渠道才有效。

（5）为体现两种回收渠道的冲突性，参考文献［16］对混合销售渠道下的市场需求函数的设计方法，对于bm＞br，可设零售商的废品回收量Gr＝θ0＋θ1br＋θ2（br－bm），制造商的废品直接回收量Gm＝θ2（bm－br）。

如果bm≤br，则Gm＝0，Gr＝θ0＋θ1br，此时回收渠道退化至单渠道模式。其中：θ0＞0表示基本回收量，代表了消费者的环保意识水平［17］；θ1＋θ2表示消费者对零售商回收价格的敏感系数，且θ1＞0，θ2＞0，θ2表示消费者对制造商与零售商回收价格差的敏感系数，显然，θ2越大，两种回收渠道之间的冲突性就越大。

（6）其他合理假设有cn＞cs，wn＞ws，pn＞ps。

2 定价模型分析

2.1 Stackelberg博弈定价

在双渠道回收模式下，制造商和零售商均以自身利润最大化原则进行决策，制造商为市场主导者，零售商为跟随者，在完全信息下，二者通过Stackelberg博弈确定相应的最优定价，如图1所示。

制造商和零售商的利润分别为：

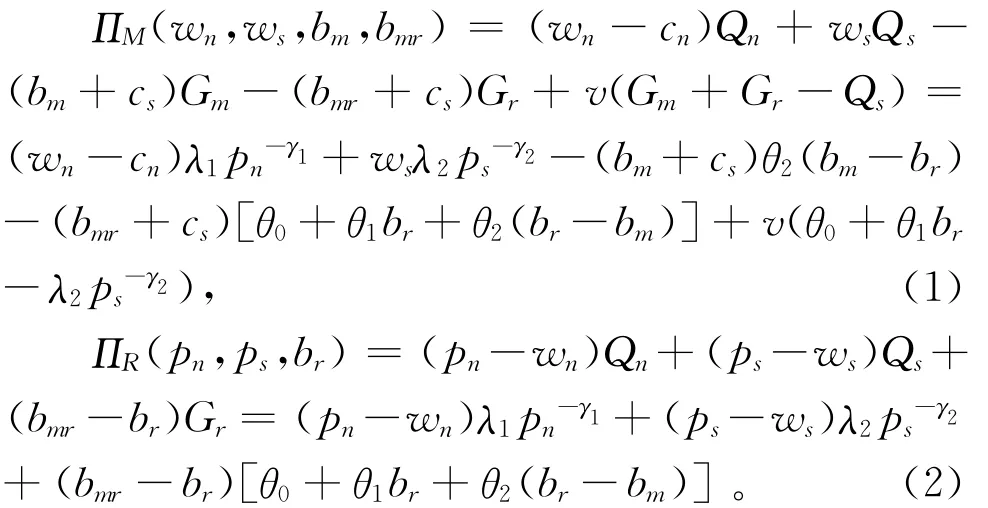
下面运用逆序归纳法求解。首先对于式（2），根据一阶优化条件确定零售商的最佳反应函数：

将上述结果代入式（1），制造商根据自身利润最大化可确定出相应的最优定价：

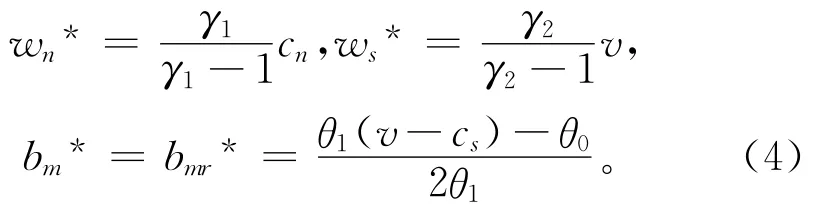
再将上述最优定价代入式（3），得到零售商的最优定价：

从而可得Stackelberg博弈模型（下称“SG模型”）下制造商和零售商的最优利润分别为：

命题1

（1）若再制造品的边际生产成本增加，则其批发和零售价格不变化，但废品回收价格均降低，各成员利润均减少。

（2）若新产品的边际生产成本增加，则其批发和零售价格均提高，各成员利润均减少。

（3）当残值v提高时，废品回收价格均上升，再制造品的批发和零售价格也随之增加，而各成员利润均是关于参数v的严格上凹曲线。

（4）若消费者的环保意识水平θ0提高，则废品回收价格均降低，各成员利润得以提升。

（5）当消费者对回收价格差的敏感系数θ2变大时，制造商的回收价不变，而零售商的回收价将增加；同时，制造商和系统总利润均提高，零售商的利润降低。

命题1的结论表明，再制造成本的增加会影响制造商废品回收的积极性，它愿意支付的回收价会降低，废旧品回收量必然减少，从而使再制造品细分市场有所损失，即便回收成本降低，仍然导致各成员利润缩减；残值的增大将激励企业为了回收更多的废旧品而提高废旧品回收价格，从而使再制造品的售价也会随之提高；消费者环保意识的增强有利于企业节约回收成本，提高企业进行回收再制造的积极性，促进闭环供应链成员具有正的社会外部性。为此，政府可以加大环保宣传力度和出台相关法律法规，以提高消费者的环保意识水平和企业的社会责任；若消费者对回收渠道间价格差的敏感程度增大，则回收渠道之间的冲突性将促使零售商提高回收价，导致零售商利润下降。作为供应链主导者的制造商，其回收价格不受影响，所建立的两条回收渠道不仅增加了自身利润，还增加了供应链的整体利润。因此，无论是零售商加价回收还是制造商“以旧换新”等形式的直接回收，都将给消费者带来实惠，也有利于闭环供应链的良性发展和稳定运行。

2.2 联合决策定价

闭环供应链上的制造商与零售商以系统利润最大化为目标，通过联合决策确定价格。此时，制造商与零售商为一个联合体，只存在单渠道回收模式（如图2），因此废旧产品的回收价格bmr＝0，bm＝br，回收量GJ＝θ0＋θ1br。

供应链系统利润为

从而可得联合决策模型（下称“JD模型”）下，供应链系统的最优利润为

命题2说明联合决策下的回收价格较高，市场上可以回收到更多的废旧品，而产品的零售价较低，有利于提升产品的市场销量，因此联合决策下的系统利润水平达到最高，相关均衡结果均严格优于Stackelberg博弈定价模型下的水平。为了达到供应链成员联合决策的均衡水准，拟构建收入－费用共享契约和两部收费制相结合的协调定价机制，以实现闭环供应链系统的全局协调和供应链成员的完美协调。

3 组合协调定价

3.1 收入－费用共享契约

在闭环供应链中，由于回收费用的存在，传统的收入共享契约不能达到协调闭环供应链的效果。近年来，有若干学者将其形式改进为收入－费用共享契约［6，10］，用作协调单回收渠道的闭环供应链，即制造商不但要与零售商分享产品销售收入，还要以相同比例分享废品回收费用。为此，本文将针对双回收渠道模式下的闭环供应链，运用收入－费用共享契约进行研究。

假设零售商和制造商分别以β和1－β的比例分享制造商的残值收入和零售商的销售收入，同时二者也以相应比例分担废旧产品的直接回收费用。对于废旧产品的间接回收费用bmrGr，因为它属于整个供应链的内部费用，这一点形同再制造品的批发费wsQs，故不纳入分享范围。此时，制造商和零售商的利润分别为：

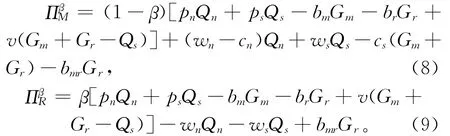
运用Stackelberg博弈模型的逆序归纳法，分别对式（9）中的pn，ps，br求一阶优化条件，可得零售商的最佳反应函数：

从式（11）可以看出，制造商作为主导者，决定将新产品以低价wβn批发给零售商，并以零价格wβs将再制造品批发给零售商作为回报，bβmr＜0表明制造商要求零售商补贴其间接回收成本。由于制造商直接回收价格与零售商回收价格持平，其回收产品主要从零售商手中间接回收得到，零售商以“零价格”从制造商手中拿到的再制造品越多，说明零售商返回给制造商的废旧品越多，也就意味着它支付给制造商的补贴越多。因此，在该契约框架下，双方为了获取最大利润，任何一方都不会出现恶意索取补贴或囤积再制造品的情形。如果零售商选择接受收入－费用共享契约，则二者可以通过分享制造商的残值收入和零售商的销售收入来保证利润的获得。此时，制造商的利润为

上述结果表明，制造商与零售商的利润之和达到了联合决策下的最优水平，即

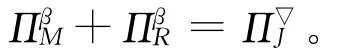
因此，收入－费用共享契约首先实现了供应链系统的全局协调，但从制造商和零售商的利润函数表达式上来看，零售商获得的利润高于收入－费用的分享比例。这也说明了由于产品的差异化销售和回收渠道间的冲突性，使得制造商的利润并没有达到最大值，作为闭环供应链的主导者，制造商一定会致力追求最大的利润。

3.2 两部收费制

基于上述分析，在收入－费用共享契约能够达成供应链全局协调的情况下，下面应用“两部收费制”的思想，对闭环供应链进行完美协调，协调过程如下：

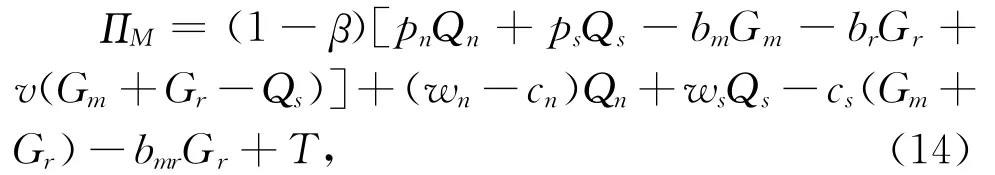
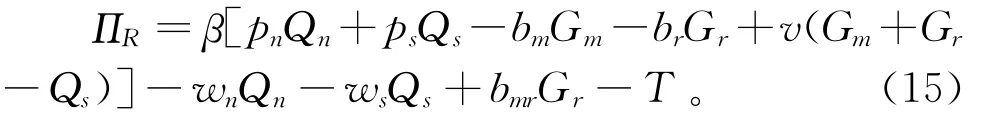
其中，T为制造商向零售商收取的作为零售商销售和回收产品的资格代理费，按照全局协调下的利润函数表达式（式（12）和式（13）），制造商只需将零售商的资格代理费决策为

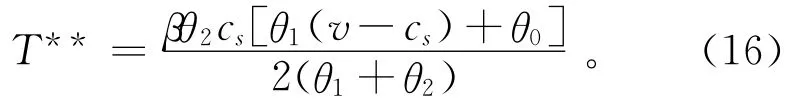
则在收入－费用共享契约和两部收费制的组合协调模型（下称“MC模型”）下，制造商和零售商的最优利润分别为

此时，制造商的利润得以提高，制造商和零售商分别以1－β和β的比例分享整个闭环供应链的利润。因此，MC模型下的系统最优总利润Π＊＊＝＋＝。

命题4 比较SG模型与MC模型的结果，可得如下结论：

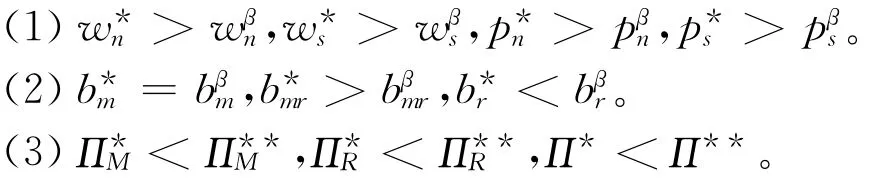
命题4说明组合协调定价使得供应链成员的决策结果显著优于Stackelberg博弈定价结果，达到了联合决策下的最优水平，此时系统总利润最高，供应链各成员的利润均高于协调前分散决策下的水平，即MC定价机制实现了闭环供应链系统的完美协调。

4 数值算例

前面已经讨论了三种模型下性能参数对回收价、成员利润和协调结果等的影响，下面将通过数值算例作进一步分析和验证。

假定θ0＝10，θ1＝2，θ2＝3，cn＝50，cs＝20，v＝30，λ1＝500，λ2＝100。对于γ1，γ2＞1，给出新产品、再制造品的销售价格敏感系数对供应链成员利润的影响（如图3）。可见，不论新产品还是再制造品，其价格敏感系数越大，市场需求量就越低，相应的成员利润都会缩减。因为零售商最接近消费市场，所以这种弹性需求对零售商的影响最大，这也是零售商利润水平整体上低于制造商以及变化幅度较大的一个原因。当价格敏感系数都超过1.5时，利润降幅非常缓慢，逐渐趋于平稳状态。为体现一般性，以下算例中γ1，γ2均取为1.5。

依据上述假定，保持其他参数赋值不变，以5为一个步长对残值v作灵敏度分析（如图4）。显然，随着残值的增大，制造商和零售商的利润曲线均为下降的凹曲线，这也印证了命题1的结论（3）。究其利润下降原因，主要是因为残值增大导致再制造品的批发价和零售价上升，再制造品需求减少，增加的残值收益不足以抵消减少的再制造品销售收益。毕竟，真正能将再制造品销售出去，肯定比保有未售出的残值要好。这一切都需要政府政策的大力支持和正确引导，需要消费者的环保意识和对再制造品认可程度的提高，需要有关行业标准的建立健全和有力执行，以及国家绿色GDP的提高和整个社会的可持续发展才能畅通无阻。

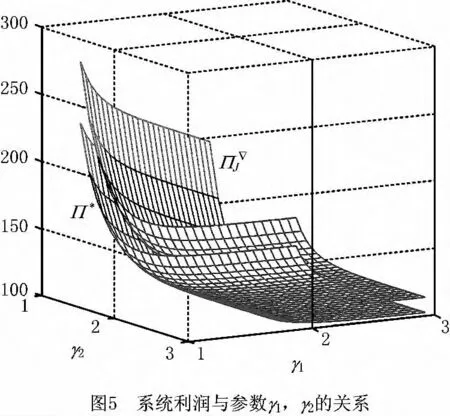
在SG模型和JD模型下，同时考察γ1，γ2对系统总利润的影响（如图5）后发现，随着γ1和γ2的增大，由于新产品和再制造品的市场需求会减少，导致Π＊，Π▽J也随之减少。而且无论γ1和γ2如何变化，JD模型下的系统利润都显著高于SG模型下的利润水平，说明联合决策有利于提高渠道效益。另外，利润凹曲面的走势表明，当γ1较大而γ2较小时，再制造品需求对新产品需求有“弱挤兑效应”，总体利润都不高；当γ1较小而γ2较大时，新产品需求对再制造品需求有“强挤兑效应”，总体利润都很高，反映了再制造品销售市场的局限性。

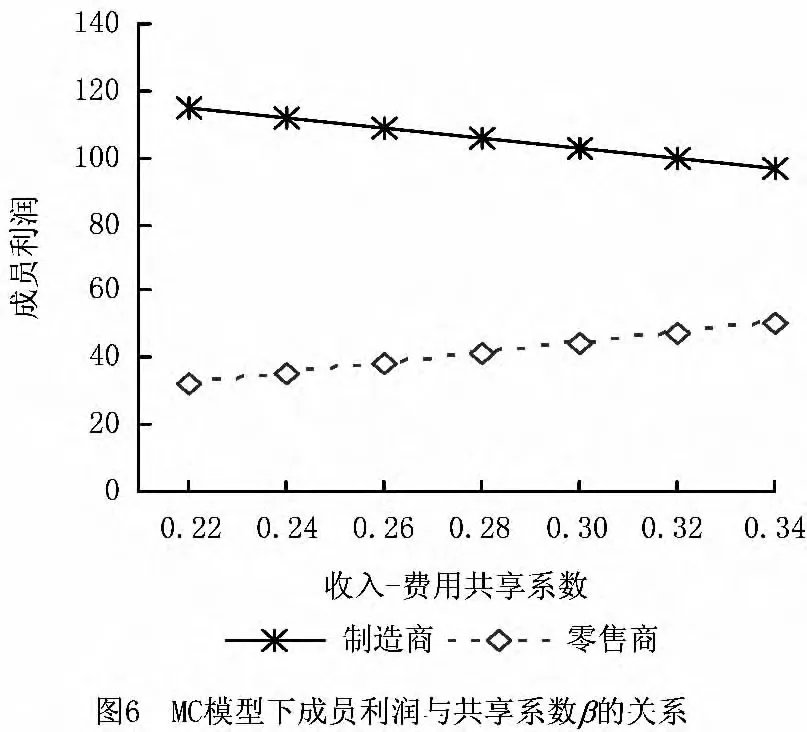
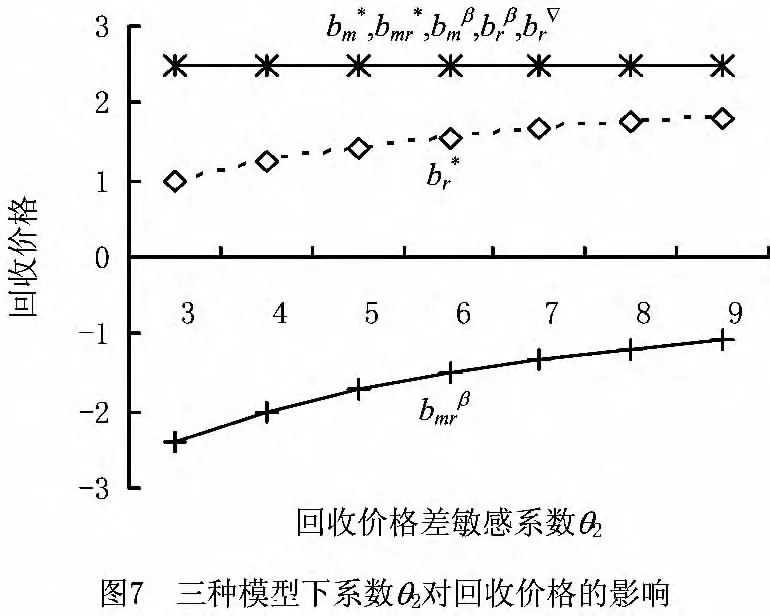
下面分析回收渠道的冲突性对回收价格的影响，对β＝0.3，若θ2以0.2为一个步长取值，则可以得到三种定价模型下回收价格的变化趋势（如图7）。可以发现，图7首先验证了前面相关命题的成立。另外，随着消费者对回收渠道间价格差的敏感程度的增大，回收渠道之间的冲突和竞争程度加剧，在SG定价模型下，制造商为了回收更多的废旧品，需要制定高于零售商的回收价格，导致零售商也相应提高回收价格，以增加废旧品回收量。在联合决策时，拥有资源集成优势的联合体可以较高的回收价格回收更多的废旧品，这样有利于促进回收再制造供应链的良性发展。在组合协调定价时，回收价格仍然能够保持联合决策下的水准，其中制造商间接回收价格的爬升曲线意味着零售商需要支付的补贴减少，说明MC定价机制能够较好地规避回收渠道之间的冲突与竞争，有利于促进闭环供应链成员实现双赢。

5 结束语

本文研究了单周期闭环供应链系统的定价与协调问题，由于新产品和再制造品的差异化定价、两类产品的弹性需求以及制造商两条回收渠道的冲突性，本研究中的供应链定价非常重要，这将直接关系到链上成员的利润。研究结果表明，若零售商愿意支付一定的资格代理费，则组合协调机制可以促成二者联合决策定价，渠道效益显著提高，能够实现制造商和零售商的双赢。另外，通过对成本参数与定价、利润等关系的理论分析和算例考察，均得到了一些有意义的结论，这为闭环供应链的发展和决策提供了一定的理论借鉴。对于闭环供应链的多周期情形以及异质产品竞争性需求的考察，将是下一步的研究方向。

［1］ HAMMOND D，BEULLENS P.Closed－loop supply chain network equilibrium under legislation［J］.European Journal of Operational Research，2007，183（2）：895－908.

［2］ TURAN P，TOLGA B，ERENÖ.Operational and environmental performance measures in a multi－product closed－loop supply chain［J］.Transportation Research Part E：Logistics and Transportation Review，2011，47（4）：532－546.

［3］ MITRA S，WEBSTER S.Competition in remanufacturing and the effects of government subsidies［J］.International Journal of Production Economics，2008，111（2）：287－298.

［4］ TSAI 段 .The study of production and inventory policy of manufacturing－remanufacturing environment in a closed－loop supply chain［J］.International Journal of Sustainable Engineering，2011，4（4）：323－329.

［5］ GUIDE 段 R，HARRISON R H，VAN V N.The challenge of closed－loop supply chain［J］.Interfaces，2003，33（6）：3－6.

［6］ SAVASKAN 段 ，BHATTACHARYA S，WASSENHOVE S W.Closed－loop supply chain models with product remanufacturing［J］.Management Science，2004，50（2）：239－253.

［7］ LIANG 段 ，POKHAREL S，LIM P K.Pricing used products for remanufacturing［J］.European Journal of Operational Research，2009，193（2）：390－395.

［8］ WEI J，ZHAO J.Pricing decisions with retail competition in a fuzzy closed－loop supply chain［J］.Expert Systems with Applications，2011，38（9）：11209－11216.

［9］ SHI 段 ，ZHANG Z A，SHA S A.Optimal production and pricing policy for a closed－loop system［J］.Resources，Conservation and Recycling，2011，55（6）：639－647.

［10］ GUO Yajun，ZHAO Liqiang，LI Shaojiang.Revenue－and－expense sharing contract on the coordination of closed－loop supply chain under stochastic demand［J］.Operations Research and Management Science，2007，16（6）：15－20（in Chinese）.［郭亚军，赵礼强，李绍江.随机需求下闭环供应链协调的收入费用共享契约研究［J］.运筹与管理，2007，16（6）：15－20.］

［11］ YI Yuyin，YUAN Jiang.Pricing coordination in closed－loop supply chain with hybrid recovery channel［J］.Management Review，2011，23（11）：169－176（in Chinese）.［易余胤，袁江.基于混合回收的闭环供应链协调定价模型［J］.管理评论，2011，23（11）：169－176.］

［12］ YI Yuyin，CHEN Yuexiao.Closed－loop supply chain models under uncertain demand［J］.Computer Integrated Manufacturing Systems，2010，16（7）：1531－1538（in Chinese）.［易余胤，陈月宵.需求不确定条件下的闭环供应链模型［J］.计算机集成制造系统，2010，16（7）：1531－1538.］

［13］ SAVASKAN 段 ，WASSENHOVE W S.Reverse channel design：the case of competing retailers［J］.Management Science，2006，52（1）：1－14.

［14］ WEBSTER S，WENG 段 .A risk－free perishable items returns policy［J］.Manufacturing and Service Operations Management，2000，2（1）：100－106.

［15］ TSAY 段 .Risk sensitivity in distribution channel partnerships：implications for manufacturer return policies［J］.Journal of Retailing，2002，7（8）：147－160.

［16］ SEONG 段 ，HEAN H A.Modelling hybrid distribution channels：agame－theoretic analysis［J］.Journal of Retailing and Consumer Service，2003，10（3）：155－167.

［17］ ZHU 段 ，SARKIS J，CORDEIRO J，et al.Firm－level correlates of emergent green supply chain management practices in the Chinese context［J］.Omega，2008，36（4）：577－591.