局部回归残余克里格对土壤阳离子交换量空间预测的精度分析

王 库，江振蓝

(闽江学院 地理科学系，福建 福州 350108)

阳离子交换量(cation exchange capacity，CEC)是指土壤胶体所吸附的各种阳离子的总量，常作为评价土壤保肥能力的指标。它是土壤缓冲性能的主要来源，也是改良土壤和合理施肥的重要依据[1－2]。CEC与土壤的胶体类型(如有机质)、pH、土壤质地(如粘粒)等密切相关，这些因素又多取决于地形、母质、植被、土壤侵蚀状况等环境要素[3－6]，因而土壤CEC在空间上的变异存在复杂性和不确定性。空间插值技术一直是研究土壤空间变异的重要手段，克里格法，如普通克里格(ordinary Kriging，OK)、回归克里格(regression Kriging，RK)等、线性回归法，如最小二乘法(ordinary least squares，OLS)等在土壤科学的研究中得到了非常广泛的应用[7－8]。OK法作为一种依靠目标变量的插值方法，依赖样品在空间上的数量和密度，忽略了影响土壤性质的环境因素，且插值效果过于平滑，存在局限[9－10]。RK法则克服了OK的缺点，模型中引入了环境要素的影响，可提高预测精度[11－13]。RK法的基本思路是首先进行环境要素与目标变量的OLS分析，先分离出目标变量中的趋势部分，然后将回归后的残差(空间结构部分)进行OK插值，最后将趋势部分与残差插值部分相加，从而得到对目标变量的空间预测结果。RK中使用的OLS是一种全局回归分析，即其回归系数在空间上是相同的。近几年广泛使用地理权重回归(geographically weighted regression，GWR)是基于环境变量与目标变量之间的一种局部回归分析方法，即回归系数在空间不同位置是不同的，被广泛用来进行空间非稳定性问题的探讨[14－17]。受此方法启发，本文尝试将RK回归中的OLS部分用局部回归的GWR加以替换，而残差部分依然采用OK插值。通过利用易获取的环境变量，在已有样本数据的基础上，利用OLS+OK(即RK)法及GWR+OK(下文简称GK)的方法，对研究区土壤表层的CEC空间分布特征进行分析，并将RK、GK、GWR及OLS的插值结果进行对比分析，分析它们精度水平、制图特点，为提高区域土壤属性预测的精度及制图提供方法参考。

1 研究区概况

研究区位于福建省闽候县旗山北麓。概略位置为东经118°51'～119°25'，北纬 25°47'～ 26°37'，总面积为 290 km2。区内地势东、南、西部三面环山，地势较高，北部及中部较低，海拔高程在180～940 m，平均高程为380 m，为典型的低山丘陵区(图1)。该区的土地利用方式主要以自然生长林地和灌丛为主(主要为次生林);区内植被覆盖状况较好，但仍有部分区域有土壤侵蚀发生;土壤类型以红壤为主。

图1 研究区概况及采样点分布Fig.1 The study area and sampling sites

2 数据源及研究方法

2.1 数据源

土壤CEC样本数据:2011年11月，采用随机采样法，采取表层0～20 cm的土壤样品个数为136个(图1)，采样的同时利用Garmin GPS定位样点的经纬度坐标及高程。每个样点取1 kg混合样。样品带回实验室经风干、研磨、过筛后，采用乙酸铵交换法测定土壤CEC[18]。

本文用到的原始数据包括:研究区的数字高程模型(DEM，GRID格式，分辨率为30 m×30 m)、ETM+(2009年1月)、河流矢量数据(.shp格式)及区内的土壤侵蚀强度数据(.shp格式)。由此派生出可能与土壤CEC相关的环境要素有海拔高程、坡度、样点至河流的最近距离 (DIST)、土壤侵蚀强度指数(SEI)，及若干光谱指数，具体包括归一化植被指数(NDVI)、亚铁矿物指数(FMI)、铁氧化物指数(IRON)、粘土矿物指数(CLAY)。

其中海拔高程由DEM直接读取;坡度由ARCGIS的空间分析模块计算而来;样点到河流的最近距离是在ARCGIS下用DISTANCE函数通过计算样点到河流的最近欧几里德距离得到;SEI由区域土壤侵蚀强度图转化而来，土壤侵蚀等级共6级，分别为无侵蚀、轻度侵蚀、中度侵蚀、强度侵蚀、极强侵蚀和剧烈侵蚀[19]。NDVI用ETM+影像的(Band5－Band4)/(Band4+Band5)计算而来，它与植被的分布密度密切相关，在一定程度上可反应出土壤有机物质含量的高低[20－21]。FMI由ETM+影像的Band5/Band4计算得到，它反映的是Fe2+所占的比例，土壤中Fe2+比例越高，则FMI的值越大，表明土壤还原程度高;IRON由ETM+影像的Band3/Band1计算得到，反映的是Fe3+所占的比例，土壤中Fe3+比例越高，则IRON的值越大，表明土壤的氧化程度高[22－23]。采用FMI及IRON两个指数主要是考虑土壤的CEC与土壤的氧化还原状况有密切相关。CLAY用ETM+影像的Band5/Band7，它主要反映粘土矿物的含量特征，CLAY值越大，则粘土矿物的含量越高[24]。

2.2 研究方法

RK的基本思路是首先在辅助变量和目标变量间进行回归分析，将回归的趋势项进行分离，对分离趋势项后的残差进行OK插值，最后将回归预测的趋势项和残差的OK估值项相加，从而得到对目标变量的估测值。RK可用下式表示:

式(1)中，Z(x0)表示对目标变量在x0处的估测值，^m为趋势项，用OLS进行拟合;^e为残差项，用OK法进行预测。由式(1)可以看出，RK综合了基于辅助变量(如高程、坡度、NDVI等)对目标变量的回归解释和OK对残差的空间结构分析，即确定性的趋势信息由回归部分加以解释，而代表空间结构部分的残差则由半方差函数进行线性无偏估计。

GWR+OK法(以下简称GK法)，即将RK中的OLS全局回归部分用GWR的局部回归加以替换。

GWR是对OLS的扩展，其回归系数在空间上随空间位置变化而变化。基本思路是样点对其附近点的影响要大于离其较远的点。特定空间点位i的回归系数不再是利用全局信息获得，而是利用邻近观测值的样本数据进行局部回归估计得到的。系数βj在空间上随地理位置变化而变化，GWR模型可以表示为:

式(2)中，y因变量，x因子变量，ε为误差项目;(ui，vi)为第i个样点的坐标，βk(ui，vi)是第i个样点上的第k个回归系数，是地理位置的函数。GWR模型中的系数估计采用加权最小二乘法实现，每个点的系数用矩阵形式表述为:

式(3)中，W(ui，vi)为m×m的空间权重对角矩阵，X为m×(n+1)自变量矩阵，Y为m×1因变量向量。空间权重矩阵的估算由高斯函数来实现:

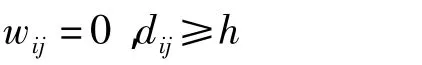
式(4)中，wij为用空间已知点j去估计待测点i时的权重，dij为被插值点i与样点j间的欧氏距离，h为带宽。该函数为距离衰减函数，距离i点越近的观测值重要性越大，反之越小。当样点至待测点的距离等于或大于带宽时，权重都被赋予为0。带宽采用最小AIC信息准则(Akaike information criterion)进行判断[25]。其表达式为(公式5):

式(5)式中:n为数据点的数量，σ’为误差项(估值标准偏差)，Tr(S)为帽子矩阵的迹。有关更为详细的GWR方法描述，可参考Fotheringham等[26]出版的教材。

2.3 精度评价

在RK中，利用线性回归模型通过环境因子估测土壤CEC的回归表现，本文采用调节决定系数(Adj－R2)进行评价。

为比较RK与GK的插值精度，在136个采样点数据中，随机均匀地抽取40样点作为验证样点，它们不参与插值过程，利用其余96个采样数据进行RK和GK插值。通过验证点处土壤CEC的实际观测值和预测值来进行预测精度评价，具体采用平均误差(ME)和均方根误差(RMSE)两个指标，其相应的公式为:

上面二式中，n为验证点的个数，z(ui，vi)和z*(ui，vi)分别为样点处的实测值和预测值;(ui，vi)为位置的坐标值。另外，在验证点上的预测值与实测值之间的相关系数(Adj-R2)也被用来评价RK格及GK的估值效果。此外，GWR与OLS的制图效果及插值精度，也纳入了本文的比较之列。

2.4 空间插值、数据处理及统计工具

回归残差的克里格拟合及插值采用地统计软件GS+GeoStatistics 7.0;GWR及OLS回归分析、制图及相关数空间数据的前处理由ARCGIS 9.3完成;ERDAS IMAGINE 8.5被用来计算NDVI、FMI、IRON及CLAY等本文用到的相关指数;传统的统计分析由PASW Statistics 18.0软件完成。

3 结果分析

3.1 土壤CEC的描述性统计

表1对待插值的96个土壤CEC样品进行了一般性统计。CEC含量变化在7.47～12.4 cmol/kg，平均值为10.0 cmol/kg。数据的离散程度较小(变异系数CV=11.1%)。偏度及峰度相对较小，通过K－S检验，CEC样品数据符合正态分布(P=0.410＞0.05)。

表1 土壤样品CEC的描述性统计Tab.1 The descriptive statistic of soil CEC

3.2 CEC与环境变量之间的相关与回归分析

CEC除与坡度及样点至河流的最近距离这二个地形指标的相关性未达显著水平外，与本文所选的其它5个环境因子的相关性都达到了显著水平，其中，与NDVI、亚铁矿物指数、铁氧化物指数、土壤侵蚀强度的相关性达到了极显著水平(表2)。说明土壤CEC与植被状况、土壤物质组成密切相关;CEC与土壤侵蚀状况呈显著负相关，因为发生土壤侵蚀的地方，多是表土有机质及细小颗粒的流失，它们是土壤负电荷的主要携带者[27－28]。

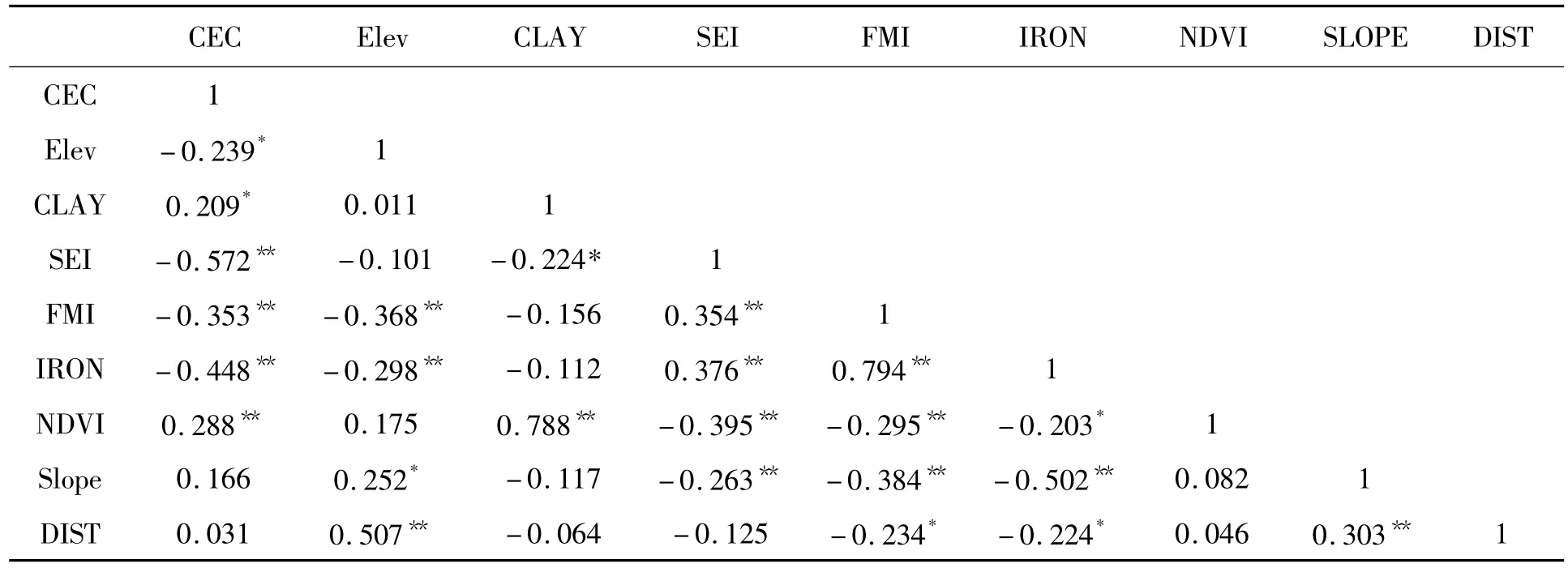
表2 表层土壤CEC与环境因子的相关性分析Tab.2 Correlations analysis between environmental factors and CEC in surface soil

由表2也不难发现，CEC除与多数环境变量有较强的相关性外，在环境变量之间也存在许多显著相关情况，如FMI与IRON，NDVI与CLYA之间的极显著相关等。因此，为减小在线性回归过程中多重共线性现象的干扰，必须对这些因子进行去共线性筛选。对因子筛选的方法是采用逐步线性回归的方式进行的。

表3 利用8个环境变量进行逐步线性回归的结果Tab.3 Results of the stepwise linear regression analysis using 8 environmental variables

通过逐步回归分析，最终得到表3的3个模型。在3个模型中，环境变量采用最多的为模型3，包括SEI、IRON和Elev，说明这3个环境因子在解释CEC的回归方程中的共线性现象较小。模型3的Adj－R2=0.452，为最大。因而本文最终采用该模型中的因子进行最终的OLS及GWR分析，由表3得到的OLS回归模型的表达式为(公式8):

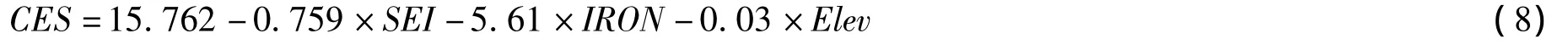
通过OLS回归发现，所选因子对土壤CEC的解释程度并不高，只有45.2%的水平。

3.3 OLS及GWR回归分析比较

利用SEI、IRON和Elev 3个环境因子，用对GWR方法对土壤CEC进行了局部回归分析。结果表明(表4)，采用局部回归的GWR方法，很大程度上降低AIC值(由OLS的264.9降低到191.6)，显著提高回归的决定系数(Adj-R2由OLS的45.2%的解释度提高到GWR的73.0%)，并且大大降低了回归的残差平方和。说明GWR能充分利用易得到的环境因子进行局部回归，在很大程度上增强了模型的回归效果，提高预测精度。另外，从2个模型中，R2到Adj-R2的较小调节幅度也表明了所选的3个变量间共线性程度处于较低水平。

表4 用相同因子分别进行OLS和GWR回归得到的相关参数Tab.4 Related parameters by using OLS and GWR model respectively with the same variables

3.4 OLS及GWR回归残差的半方差拟合及RK、GK空间插值

OLS回归后的CEC 残差介于－2.45～3.22 cmol/kg，GWR 的残差范围小于 OLS，介于 －1.73～1.51 cmol/kg。从残差的频率分布图上来看(图2)，二者都仅有一个主峰值，并且通过K－S检验，二者的残差符合正态分布(OLS残差的P=0.385＞0.05;GWR残差的P=0.319＞0.05)，满足克里格内插条件。表5是利用二者残差进行OK拟合的相关参数。

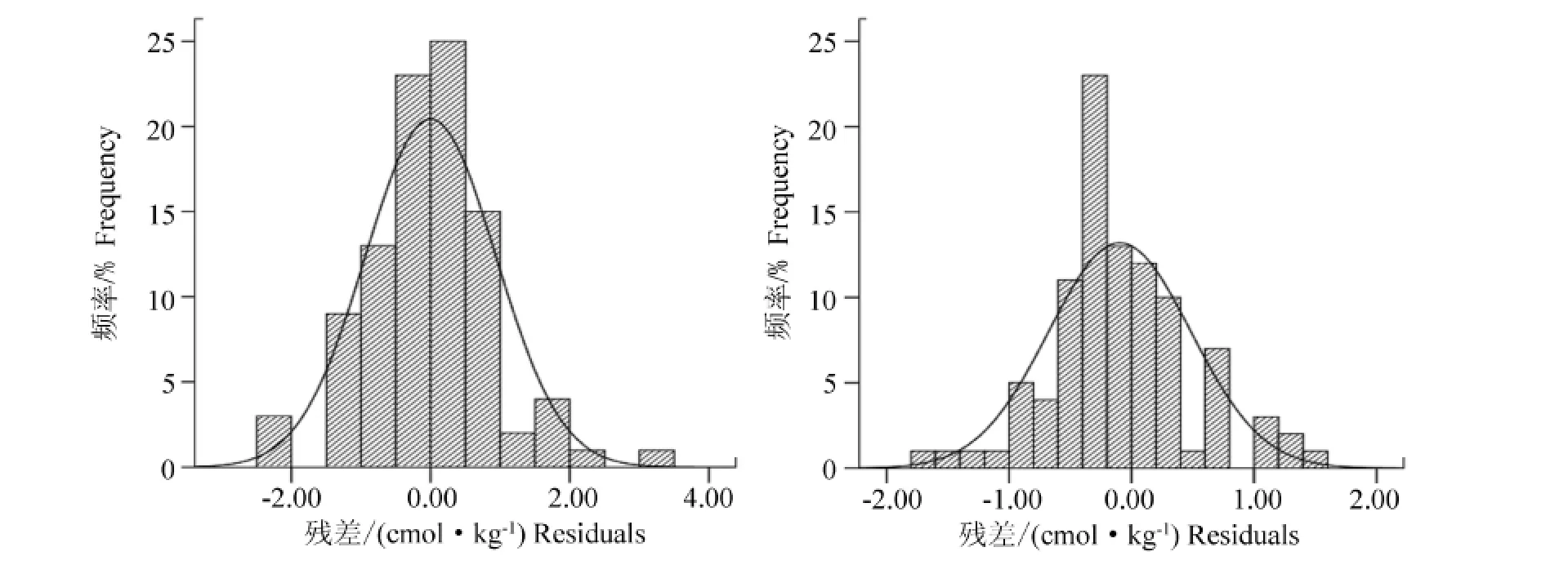
图2 OLS(左)及GWR(右)回归后的CEC残差分布频率Fig.2 Histogram of the CEC residuals from OLS and GWR regression

表5 用OLS及GWR回归后的残差拟合的半方差函数模型及参数Tab.5 Semi-variogram models and parameters fitted by using residuals from OLS and GWR regression respectively

由表5可以看出，二者的残差用指数模型拟的效果较好。较小的块金值和较高的C/C0+C值均说明二者残差部分的空间自相关性较强，随机变异较小，变异主要来自空间结构部分。从半方差函数的拟合效果来看，二都的决定系数都达到了90%以上，较好地解释了残差在空间上的变异情况，且拟合后RSS值均较小，说明拟合取得了较佳的效果。

根据二者残差半方差的拟合结果，分别利用RK和GK插值计算得到土壤CEC空间分布图。另外，为比较目的，OLS及GWR对CEC进行回归的结果也进行了制图(图3)。

从CEC分布图上看，CEC含量较高的区域主要分布中东部海拔较高、土壤侵蚀较轻的区域，而土壤侵蚀严重区域CEC含量相对较低。4幅预测图都考虑了环境因子的作用，因而在空间上的变化过渡均较为自然、平缓，CEC含量随环境要素变化特征明显，这与研究区CEC的分布实际吻合得较好。相比较而言，GK与RK更能体现CEC在空间上的细节变化。较前两者更为精细。从4幅图的表观来看，对含量较高CEC区域的预测，OLS法预测图的高值区域较少，GWR的高值处于中等程度，RK及GK的高值在中部区域较为集中，但仅此还很难区分出插值效果优劣。

图3 分别用OLS、GWR、RK及GK插值得到的土壤CEC空间分布Fig.3 Spatial distribution map of CEC interpolated by using OLS，GWR，RK and GK

3.5 OLS、GWR、RK 及 GK 精度对比

为进一步评价OLS、GWR、RK及GK这4种方法的预测效果，40个未经插值使用的样点数据用来比较它们的表现。这里，采用最大(正负)估计误差，平均误差(ME)、均方根误差(RMSE)以及40个样点处4种方法的预测值与实测值进行线性回归的调节决定系数(Adj-R2)，来评价它们的插值效果。相关参数由表6所示。

表5 用于比较OLS、GWR、RK及GK插值效果的有关参数Tab.5 Related parameters for comparing of the performances of OLS，GWR，RK and GK cmol/kg

如果预测误差是无偏的，预测值与实测值接近，ME接近于0。RMSE则揭示的是预测值的精度水平，该值应越小精度越高[29]。由表6知，4种方法的ME以GK法为最低，依次为GK＜GWR＜RK＜OLS，说明GK的估计与实测值最为接近。通过均方根误差RMSE的比较，也是GK法为最低，其精度最高，GWR次之，以OLS的精度为最低。这点也可从最大正(负)误差中得以体现，GK的最大正(负)误差均为最小，与RK法极为接近。另外，通过对4种方法的预测值与实测值分别进行线性回归比较，发现GK法得到预测值的回归决定系数为0.897，说明用GK法所选的环境因子对土壤CEC的解释程度可达近90%水平，与GWR相比，其解释程度提高了9%，说明提高部分是由回归残差的空间结构变异引起的。RK法得到的预测值在与实测值进行回归时，其回归的决定系数为0.833，仅次于GK法，但远远高出OLS的回归值，通过OLS回归的残差中空间结构部分的解释程度占了34.4%。由此可以判断，在提高精度的水平上，RK法比单独的OLS更能大幅提高预测精度，这种效果明显高于GK，这主要因为GK在回归的过程中，本身就是一种局部回归方式，在其残差中仅存少量的空间结构变异，但采用GK法可以起到精益求精的效果。

4 讨论与结论

土壤CEC及多数土壤属性客观上受众多环境因素的作用，在不同空间位置作用上环境因素也不尽一致，因而其空间分布多数情况下并不满足平稳假定，而呈现空间非稳定性特点[30－31]。GWR法是通过建立因变量(CEC)与环境因子之间的回归方程，采用局部回归的方式进行的空间插值，因而其预测结果的精度较OLS方法有较大的提升。因此，GK方法通过GWR回归，再加上对其回归残差的结构性解释，使其精度较RK及GWR均有一定程度的提升。另外，在GWR分析中，应充分考虑回归模型多重共线性现象。在回归之前，应进行必要的共线性检验(如方差膨胀因子检验、蒙特卡罗检验等)，必要时可将某些因子进行适当的数学转换(如对数转换、正余弦变换等)，以消除多重共线性现象的干扰。

通过上述不同方法对表层土壤CEC空间插值精度的比对，得出以下结论:用到的4种插值方法，都能充分利用CEC与环境因子之间的相关关系，插值精度以GK为最高，依次为GK＞RK＞GWR＞OLS。制图效果上，RK及GK更能体现CEC在空间上的变化细节，是土壤属性预测的可靠方法。GK法可以充分利用容易获取的环境因子信息，适用于具有空间非稳定分布的土壤属性空间预测及制图。

[1]黄昌勇.土壤学[M].北京:中国农业出版社，2000:158－169.

[2]Renault P，Cazevieille P，Verdier J，et al.Variations in the cation exchange capacity of a ferralsol supplied with vinasse，under changing aeration conditions:Comparison between CEC measuring methods[J].Geoderma，2009，154:101 －110.

[3]沈润平，王海辉，连楚楚，等.稻田土壤有机质氧化稳定性与土壤肥力关系的研究[J].江西农业大学学报，1997，19(1):1－4.

[4]刘世全，蒲玉琳，张世熔，等.西藏土壤阳离子交换量的空间变化和影响因素研究[J].水土保持学报，2004，18(5):1－5.

[5]姜林，耿增超，李珊珊，等.祁连山西水林区土壤阳离子交换量及盐基离子的剖面分布[J].生态学报，2012，32(11):3368－3377.

[6]李海鹰，姜小三，潘剑君，等.土壤阳离子交换量分布规律的研究——以江苏省溧水县为例[J].土壤，2007，39(3):443－447.

[7]王永东，冯娜娜，李廷轩，等.不同尺度下低山茶园土壤阳离子交换量空间变异性研究[J].中国农业科学，2007，40(9):1980－1988.

[8]杨奇勇，杨劲松.基于GIS和GS+的耕地土壤阳离子交换量的序贯高斯模拟[J].中国农业科学，2010，43(18):3759－3766.

[9]李启权，岳天祥，范泽孟，等.中国表层土壤全氮的空间模拟分析[J].地理研究，2010，29(11):1981－1992.

[10]Goovaerts P.Geostatistics in soil science:State-of-the-art and perspectives[J].Geoderma，1999，89:1 －45.

[11]Li X M，Wu J J，Xu J M.Characterizing the risk assessment of heavy metals and sampling uncertainty analysis in paddy field by geostatistics and GIS[J].Environmental Pollution，2006，141:257 －264.

[12]赵永存，史学正，于东升，等.不同方法预测河北省土壤有机碳密度空间分布特征的研究[J].土壤学报，2005，42(3):379 －385.

[13]Hengl T，Heuvelink G，Stein A.A generic framework for spatial prediction of soil variables based on regression Kriging[J].Geoderma，2004，122(1/2):75 － 93.

[14]Erdogan S.Modelling the spatial distribution of DEM error with geographically weighted regression:An experimental study[J].Computer＆ Geoscieces，2010，36:34 －43.

[15]Zhang C S，Tang Y，Xu X L，et al.Towards spatial geochemical modelling:Use of geographically weighted regression for mapping soil organic carbon contents in Ireland[J].Applied Geochemistry，2011，26:1239 －1248.

[16]Tu J.Spatially varying relationships between land use and water quality across an urbanization gradient explored by geographically weighted regression[J].Applied Geography，2011，31:376 －392.

[17]Jaimes N B P，Sendra J B，Delgado M G，et al.Exploring the driving forces behind deforestation in the state of Mexico(Mexico)using geographically weighted regression[J].Applied Geography，2010，30:576 －591.

[18]张彦雄，李丹，张佐玉，等.两种土壤阳离子交换量测定方法的比较[J].贵州林业科技，2010，38(2):45－49.

[19]Wang K，Wang H J，Shi X Z，et al.Landscape analysis of dynamic soil erosion in Subtropical China:A case study in Xingguo County，Jiangxi Province[J].Soil and Tillage Research，2009，105:313 －321.

[20]连纲，郭旭东，傅伯杰，等.黄土丘陵沟壑区县域土壤有机质空间分布特征及预测[J].地理科学进展，2006，25(2):112－122.

[21]Kheir R B，Greve M H，B，cher P K，et al.Predictive mapping of soil organic carbon in wet cultivated lands using classification － tree based models:The case study of Denmark[J].Journal of Environmental Management，2010，91:1150 －1160.

[22]何挺，王静，程烨，等.土壤氧化铁光谱特征研究[J].地理与地理信息科学，2006，22(2):30－34.

[23]吕开云，胡振琪，高永光.光谱指数在铀矿找矿中的应用[J].矿业研究与开发，2006，26(4):47－50.

[24]季耿善，徐彬彬.土壤粘土矿物反射特性及其在土壤学上的应用[J].土壤学报，1987，24(1):67－76.

[25]Brunsdon C，Fotheringham S，Charlton M，et al.Geographically weighted regression-modelling spatial non-stationarity[J].Society，2010，47(3):431－443.

[26]Fotheringham S，Brunsdon C A，Charlton M.Geographically weighted regression:The analysis of spatially varying relationships[M].John Wiley ＆ Sons，New York，2002:2 －283.

[27]廖凯华，徐绍辉，程桂福，等.土壤CEC的影响因子及Cokriging空间插值分析——以青岛市大沽河流域为例[J].土壤学报，2010，47(1):26－32.

[28]许明祥，刘国彬，赵允格.黄土丘陵区土地利用及环境因子对土壤质量指标变异性的影响[J].应用生态学报，2011，22(2):409－417.

[29]Sun W，Minasny B，McBratney A.Analysis and prediction of soil properties using local regression-Kriging[J].Geoderma，2012，171:16 －23.

[30]Brunsdon C，Fotheringham S，Charlton M.Geographically weighted summary statistics-a framework for localised exploratory data analysis[J].Computers，Environment and Urban Systems，2002，26:501 －524.

[31]Yee L，Chang L M，Zhang W X.Statistical tests for spatial nonstationarity based on the geographically weighted regression model[J].Environment and Planning A，2000，32:9 －32.