利用几何画板巧解有关平面直角坐标系的问题

于江波

（沈阳师范大学教师专业发展学院，辽宁 沈阳 110034）

利用几何画板巧解有关平面直角坐标系的问题

于江波

（沈阳师范大学教师专业发展学院，辽宁 沈阳 110034）

利用几何画板获得的经验性知识，能够顺利实现数学各种类型语言之间的转化，有助于学生逻辑知识体系的建立，引导学生认知数学问题，促进学生从语言阅读开始认真观察，寻找数学量之间的关系，提高学生解决问题的能力。

几何画板；平面直角坐标系；数学问题

一、问题的提出

在北师大版八年级数学课本“平面直角坐标系”一节的习题中，曾经出现过这样一道题：传说中藏宝人生前利用平面直角坐标系画了一幅藏宝图。现今的寻宝人没有原来的地图，但知道在这图上有两块大石头A、B，坐标是（2，1）、（8，2），而藏宝地的坐标是（6，6），试设法在地图上找到藏宝地点。

在不知道平面直角坐标系（以下简称为坐标系）的前提下，已知两点坐标要想确定第三点坐标，必须找到坐标系的坐标原点、单位长度（即单位“1”）和坐标轴的方向。然而在这道问题中，A、B两点的距离经过计算是无法通过常规的方法确定其坐标系的单位“1”的长度，从而使解决这道题陷入了瓶颈。

那么如何才能在没有坐标系的情况下，通过已知的一个无理数的长度确定单位“1”的大小呢？这里我们可以通过几何画板这个软件的辅助来实现。

二、问题的解决

（一）问题分析

问题的解决需要找到：坐标原点、单位长度（即单位“1”）和坐标轴的方向，其中最关键的是确定单位“1”的长度。因为A、B两点的距离是个无理数，因此无法准确地画出单位“1”的长度。因此这里不妨利用几何画板这一动态工具来解决：以线段AB为直径作圆，在圆上任取一点P构造直角三角形ABP，使AB成为直角三角形的斜边，因此斜边长即为通过调整P点在圆上的位置使两直角边的比为6：1，那么比例为1份的那条直角边即为单位“1”的长度，解决了由于常规方法很难准确地度量出两条线段的精确比值，因而找不到单位“1”的问题。

（二）具体制作步骤

1．在几何画板中任意画两个点，标注坐标分别为A（2，1）、B（8，2）。（先假设左边点（2，1）为 A，右边点（8，2）为 B）

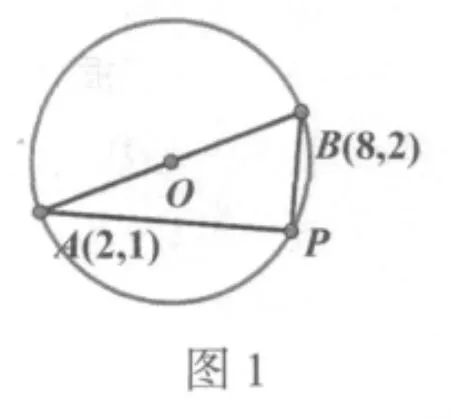
2．连接A、B两点，取线段AB的中点为O，并以O为圆心，BO为半径作圆，如图1。

3．在圆O上任选一点P（假设P点靠近B点，并在B点下方），连接PA、PB。（此时PA、PB一定是直角三角形的两条直角边）

4．度量PA、PB的长度，并计算出PA/PB的比值。（注意：始终使长边比短边）

5．如图2，调整P点的位置，使其比值恰好等于6，这时PB的长度即为单位长度。

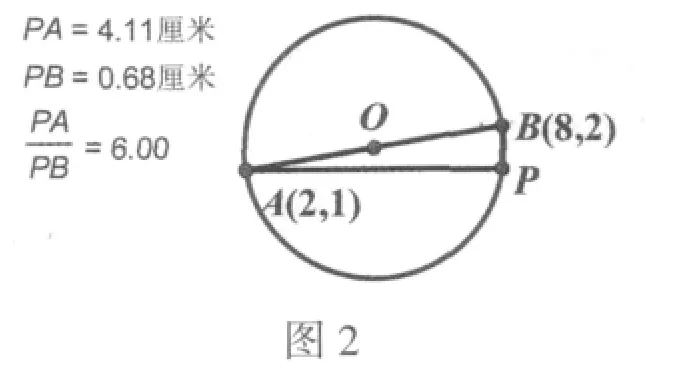
6．如图3过A点作PA的垂线a，并以A为圆心、PB长为半径画圆，此圆与直线a的交点为M，再过点M作直线a垂线，此直线即为x轴，并且取向右方向为正方向。

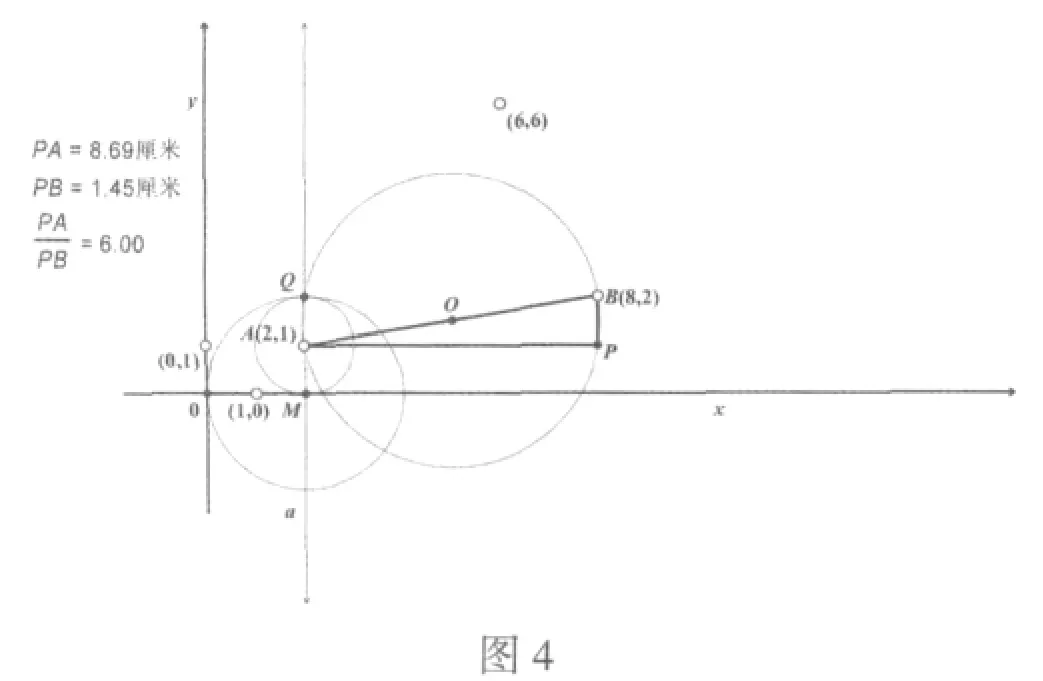
7．如图4，以M点为圆心，2MA长为半径画圆，此圆与x轴的交点即为坐标原点。（2MA长的确定方法：以A点为圆心，MA长为半径作圆，不妨设线段MA所在的直线与圆的另一个交点为Q，则MQ长就是2MA长,也就是所作圆的直径。）

8．如图4，过原点作x轴的垂线，那么此垂线即为y轴，取向上方向为正方向。到此原点、单位长度和坐标轴都确定了，找到藏宝地（6，6）点就不是问题了。

（三）关于P点存在数量问题的讨论

在前面的做法中我们假设P点靠近B点，并在B点下方，那么在B点的上方和A点的上方、下方能否找到同样符合PA/PB的比值为6的P点呢？答案是肯定的。这样P点的位置除了上面已讨论的情况外，还有三种可能的情况，下面分别讨论这三种情况是否能满足已知条件，从而确定P点存在的数量。

1．情况一

我们把在B点上方找到的点设为，那么根据之前叙述的具体操作步骤，我们找到了单位“1”并做出了坐标系，但令人费解的是A、B两点同时位于坐标系的第二象限，坐标应为负数，这与已知A、B两点的坐标都为正数相矛盾；此外，按照坐标系的性质越往正方向坐标的数值应该越大，A、B两点的位置与它们已知的坐标相矛盾，因此这种情况点是不存在的。

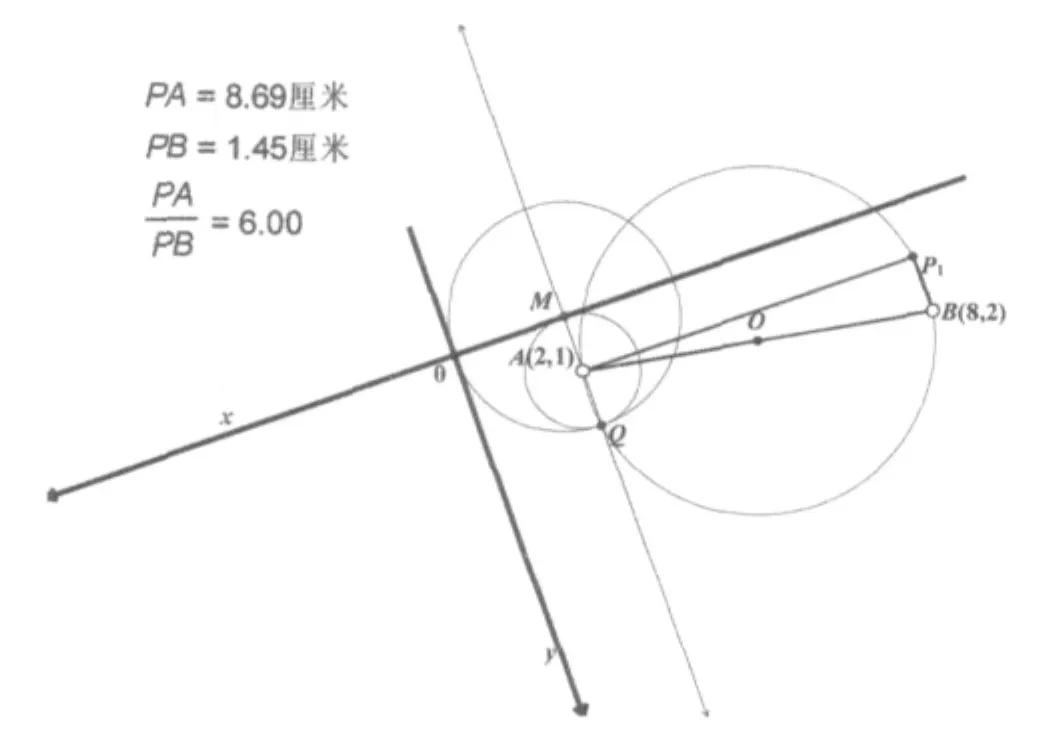
2．情况二

我们把在A点上方找到的点设为，同理根据之前叙述的具体操作步骤，我们找到了单位“1”并做出了坐标系，通过作图和观察我们发现，这种情况符合坐标系的性质以及坐标数值的大小规律。

但有一点需要注意：此时A、B两点的坐标需要对调，使 B 点坐标为（2，1）、A 点坐标为（8，2），这样才能够成立。也就是说藏宝图中没有确定A、B某一个点的坐标就是（2，1），而不可能是（8，2）时，这种情况也成立。但如果藏宝图中表明了地理方位、方向指示以及确定点的坐标表示，那么这种情况就与第一种情形取其中一种，具体哪种还要看地图中（8，2）点在（2，1）点的右边还是左边了。

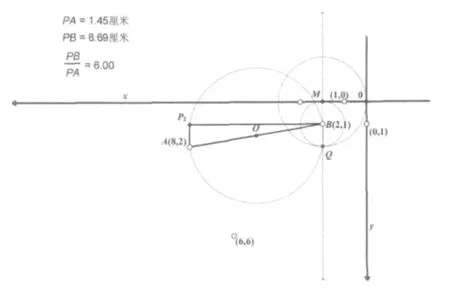
3．情况三

我们把在A点下方找到的点设为，通过作图和观察发现，此种情况与情况一类似，只是方向不同而已，因此不存在的理由也是相同的，具体作图方法和分析过程同上，此处不再赘述。

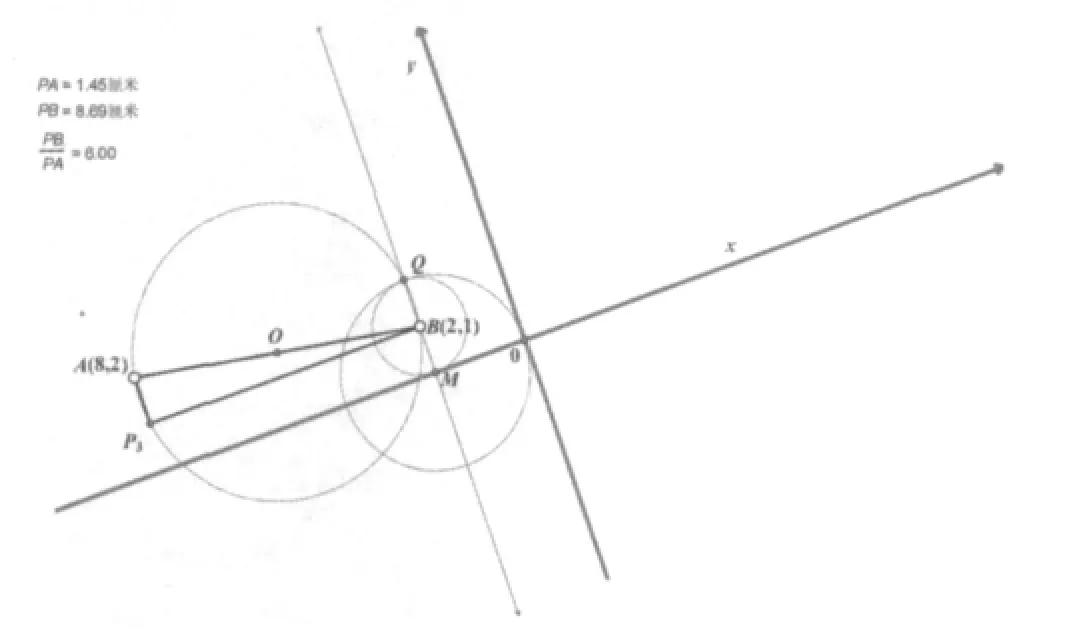
事实上我们按照上面的方法作出的四个点中只有P、符合条件，也就是说在找到坐标轴后，两点的坐标符合其在坐标轴上的坐标位置，因此满足条件的P点只有两个，也可能是一个。

三、评价与总结

通过对北师大版八年级课本有关平面直角坐标系的一道“藏宝图”问题的分析和探索，我们看到此题是一道能让学生充分体会平面直角坐标系中坐标原点、单位“1”和坐标轴方向的重要性的题目，对认识平面直角坐标系以及利用其性质去解决问题有很大的帮助。这道题之所以后来被删掉，关键是由于已知两点之间的距离是个无理数，无法通过简单常规的测量方法找到单位“1”。然而利用几何画板这一有力的工具，使这道不易解决的问题迎刃而解。

《义务教育数学课程标准（2011版）》指出：“把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式，是学生乐意并有可能投入到现实的、探索性的数学活动中去。”如果教师在数学教学中善于发挥几何画板形象化、动态化的优势，就可以像解决这个“藏宝图”问题一样，为学生创造人机交互、及时反馈的学习环境，从而改善教与学的方式，充分调动学生学习的积极性和主动性，启发、引导学生通过观察、实验、探究、猜想、验证、推理与交流等多种方式进行数学活动，积累多样化的数学活动经验，创造性地解决在学生看来难以解决的问题。

[1]瞿绍军，刘宏，刘先锋.让《几何画板》生动起来[J].中小学信息技术教育，2005（07）.

[2]杨超杰.浅谈“几何画板”及其在初中数学教学中的运用[J].中学生数理化（教与学），2009（03）.

[3]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

于江波（1969-），女，辽宁沈阳人，沈阳师范大学教师专业发展学院，讲师，硕士，研究方向为数学课程与教学论。

（责任编辑：张华伟）