某舰用燃机高压涡轮压气机转子传递矩阵建模
马 超,汤华涛,贺培文
(1.中国人民解放军91343部队,山东 威海 264200;2.海军工程大学机械工程系,湖北 武汉 430033;3.中国人民解放军91329部队,山东 威海 264200)
0 前言
燃气轮机是舰船、航空动力和工业生产中常用的一种发动机,而燃气轮机的转子是燃机的重要组成部分,国内外学者对其展开了广泛的研究。目前,学者们采用的建模方法大体可以归类为多体系统动力学、传递矩阵法和有限单元法3种。但随着计算量的加大和计算精度的不断提高,这3种方法的缺点日益突出,为了解决这些问题,必须寻找一种新的适合燃气轮机转子的计算方法。
20世纪末,芮筱亭等将多体系统动力学和传递矩阵法相结合,成功解决了复杂多体发射系统特征值问题,并首次提出多体系统传递矩阵法[1]。经过10多年的不断完善和工程应用以及广泛的国际学术交流,最终形成了较为系统的多体系统传递矩阵法。它建模灵活,简洁,程式化程度高,计算量小,已得到广泛应用。由于该方法的计算特点,它特别适合解决链式结构系统问题,如连续梁,涡轮轴等。因此,本文将选择多体系统传递矩阵法建立某燃气轮机高压涡轮压气机转子计算模型。
由于该转子的工作特点,其结构比较复杂,转子内部有多处凸起,如果采用传统的偏微分方程来推导其传递矩阵,难度太大。本文以某燃机高压涡轮压气机转子为例,利用有限元法推导转子各段的刚度矩阵,再通过矩阵变换求出其传递矩阵,最后将各段传递矩阵组合为整体传递矩阵,建立高压转子的多体系统传递矩阵模型。
1 凸起部分传递矩阵
图1为某燃机高压转子结构示意图,转子有多处凸起部分,应该先单独考虑凸起部分,分别推导其传递矩阵,然后将各段传递矩阵组合为整体传递矩阵。
可得转子的凸起部分简化为图2中结构,并以凸起中线为轴,将凸起分为左右2个部分。单独考虑凸起左半部分,将其划分为2个梁单元,编号为Ⅰ、Ⅱ,如图3所示。若只考虑梁单元的横向振动,可假设2个梁单元的刚度矩阵分别为KⅠ和KⅡ,2个刚度矩阵都是四阶矩阵[2-4],其表达式如下:

将2个梁单元的刚度矩阵集成为整体刚度矩阵[5],则可得到整体刚度方程

图1 某燃气轮机高压涡轮压气机转子Fig.1 High-pressure compressor rotor of gas turbine

图2 凸起部分结构图Fig.2 Structure of rotor with convexity

图3 凸起梁单元模型Fig.3 Model of beam element with convexity

式中:Fi和Mi(i=1,2,3)为节点i所受的力和力矩;ui和θi(i=1,2,3)为节点i的位移和转角。
假设此凸起的节点1不受力,即 F1=M1=0,则
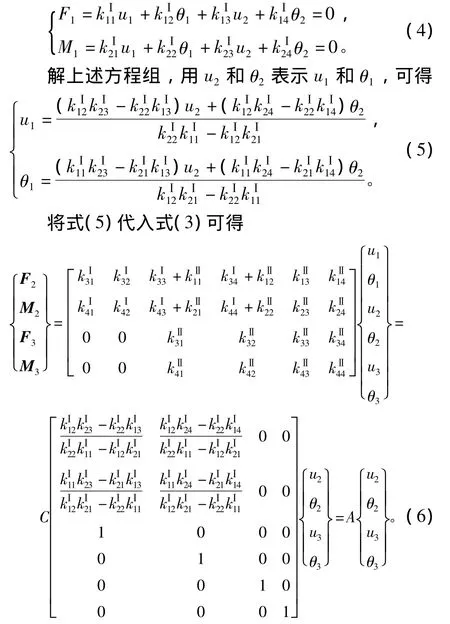
矩阵A即整个轴结构中节点2到节点3的刚度矩阵,刚度矩阵A考虑了梁单元1对整个轴结构的影响,且A为四阶矩阵,可将A写成如下形式:
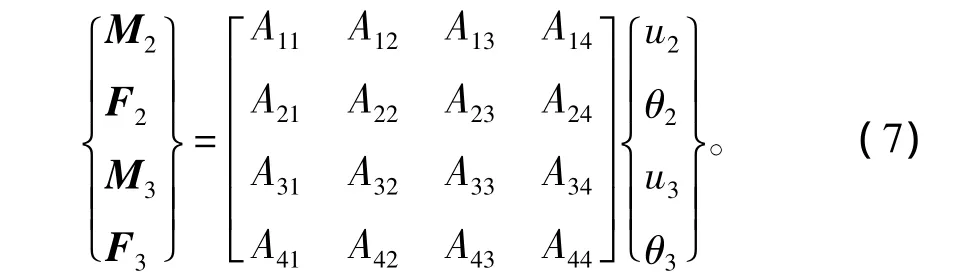
定义状态矢量 Z2={u2θ2M2F2}T,Z3={u3θ3M3F3}T,将式(7)展开,用 Z2表示Z3,则其传递方程[1]为
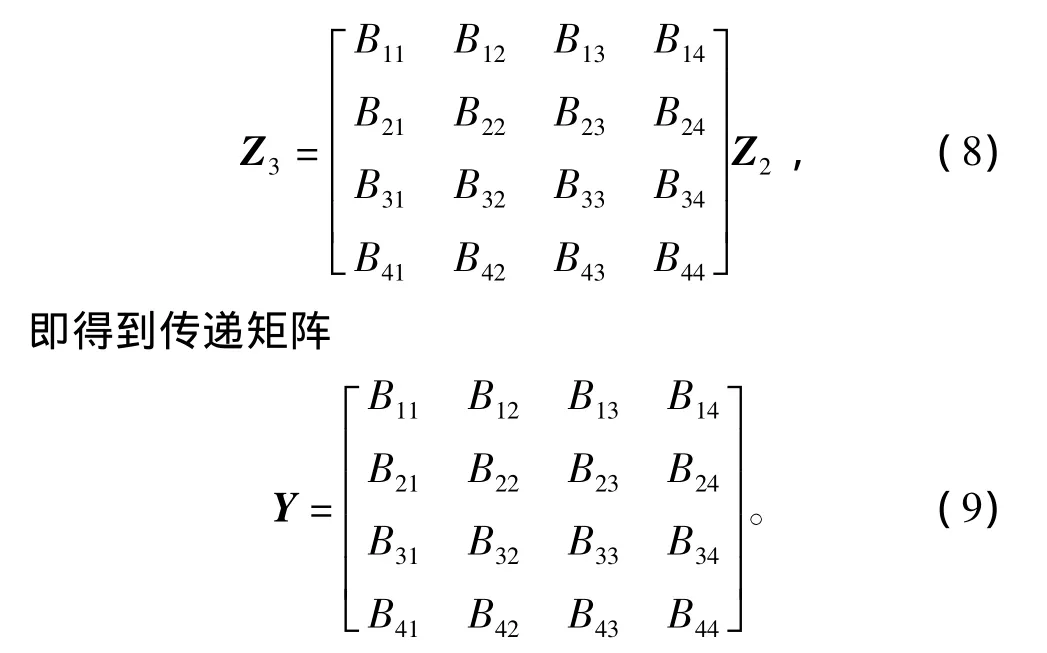
用同样的方法,可以推导出凸起右半部分的传递矩阵。
2 转子整体传递矩阵模型
转子无凸起部分的传递矩阵文献 [1]中已给出,且前文已经利用有限元法推导出转子凸起部分的传递矩阵,但由于在推导过程中使用的是无质量梁单元模型,所得到的传递矩阵也没有质量信息,无法计算其振动,因此在转子整体传递矩阵模型中必须考虑其质量。本文的处理方法是在转子各段中点处添加集中质量点,其质量为各段总质量。将图1中的转子模型分段,并依次编号为0~46,如图4所示,其中在中心线以上的编号表示集中质量点。
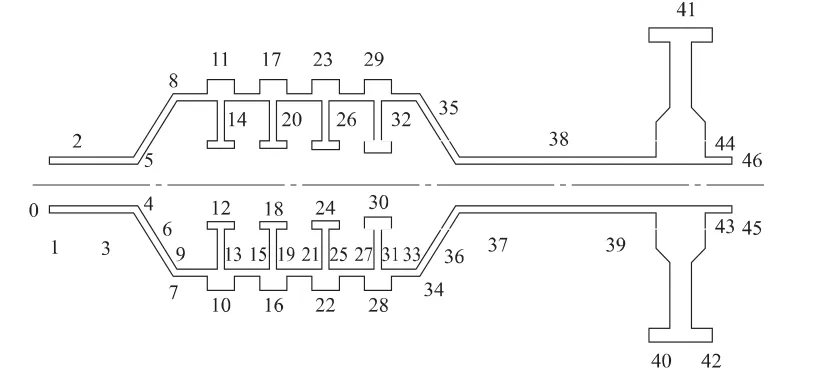
图4 转子多体系统传递矩阵模型Fig.4 Transfer matrix method of multibody system model of rotor
定义状态矢量Z0,1, Z2,1, Z2,3, …, Z44,45,Z46,45的形式均为 Z=[u,θ,M,F]T,定义各段传递矩阵U1,U2,U3,…,U45,U46,其中转子各段的传递矩阵已得到。根据多体系统传递矩阵法的知识,集中质量点的传递矩阵为[5]
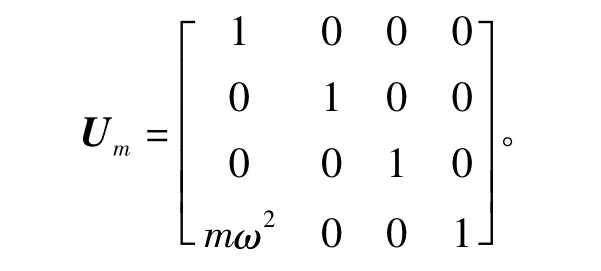
式中:m为集中质量点的质量;ω为系统固有频率。最终可得到转子的总传递方程为

已知U为四阶矩阵,设其表达式为

在此模型中,转子两端固定约束,故有:

求解式(14),即可得到系统的固有频率[6]。
3 算例分析
以图1中转子为计算模型,用多体系统传递矩阵法计算其横向振动固有频率。为了验证该方法的正确性,可与有限元软件Ansys计算结果做比较[7]。在有限元前处理时,为了保证计算精度,将转子的几何模型导入有限元软件HyperMesh中,采用六面体划分网格,单元类型选用Solid185,最后得到的转子有限元模型共有162214个单元,206196个节点。然后将有限元模型导入Ansys中,在转子的两端施加位移约束,计算其约束模态。本文只考虑转子的横向振动,在Ansys中计算转子的前20阶模态,并取出其振型为横向振动的模态,与本文方法计算结果相比较 (见表1)。

表1 计算结果对比Tab.1 Comparison of results
从表1可看出,用2种方法计算得到的转子前两阶模态频率差距很小,验证了本文方法的正确性。用Ansys软件计算时,计算过程耗时3 h,加上前处理时间,共用时10 h。本文方法从编程到计算共用时5 h,其缺点是编程和程序调试过程较繁琐,但是当方法成熟之后计算转子的其他问题就比较方便,所以本文方法比Ansys软件计算简洁方便。
本文方法还继承了Matlab自编程序灵活多变的特点,可以改进程序,控制误差,提高计算精度,还可以优化算法以减少计算时间。
4 结语
本文以某燃气轮机高压涡轮压气机转子为例,利用有限元法推导转子各段的刚度矩阵,再通过矩阵变换求出其传递矩阵,最后将各段传递矩阵组合为整体传递矩阵,建立高压涡轮压气机转子的多体系统传递矩阵模型。通过算例证明,该方法计算准确,易于实现,为用有限元法和多体系统传递矩阵法求解燃气轮机转子动力学问题提供了新思路。
[1]芮筱亭,贠来峰,陆毓琪,等.多体系统传递矩阵法及其应用[M].北京:科学出版社,2008.
[2]HOWSON R.Exact dynamic stiffness matrix for a thinwalled beam-column of doubly asymmetric cross-section[J].Structural Engineering and Mechanics,2011,38(2):195-210.
[3]李开禧,赵广坡,熊晓莉.薄壁梁的单元刚度矩阵及其应用[J].重庆建筑大学学报,2004,26(5):35 -38.LI Kai-xi,ZHAO Guang-po,XIONG Xiao-li.Element stiffness matrix of thin-walled beam and its application[J].Journal of Chongqing Jianzhu University,2004,26(5):35 -38.
[4]王勖成,邵敏.有限单元法基本原理和数值方法[M].北京:清华大学出版社,1997.
[5]芮筱亭,刘亚飞.梁系统振动的传递矩阵法[J].力学与实践,1993(5):66-67.RUI Xiao-ting,LIU Ya-fei.Transfer matrix method on vibraton of beam[J].Mechanics and Engineering,1993(5):66 -67.
[6]LOEWY R G,BHNTANI N.Combined finite elementtransfer matrix method[J].Journal of Sound and Vibration,1999,226(5):1048 -1052.
[7]关琦,金鹤,新力.某型燃气轮机低压涡轮压气机转子动力学分析[J].舰船科学技术,2010,32(8):127 -132.GUAN Qi,JIN He,XIN Li.Analysis on rotor dynamic of the low tuibocompressor[J].Ship Science and Technology,2010,32(8):127-132.

