船舶在长峰不规则波中顶浪纵向运动的数值模拟

刘 可，吴 明，杨 波

(1.中国人民解放军91550部队，辽宁 大连 116026;2.海军大连舰艇学院，辽宁 大连 116018)

0 引言

船舶航行的纵向运动主要包括船舶的纵摇及垂荡。严重的纵摇和垂荡将引起甲板上浪、砰击和失速等一系列后果，对船舶在海上的航行安全以及舰载武器的使用影响极大。因此，本文选取船舶的纵向运动作为研究对象，基于CFD方法对船模在长峰不规则波中顶浪运动进行数值模拟，具有迫切的现实意义。

1 波浪的数值模拟

要实现对船模在长峰不规则波中顶浪纵向运动的数值模拟，首要前提就是构建精度满足耐波性计算要求的长峰不规则波数值波浪水池。所谓的数值波浪水池，是指对非线性波浪水动力以及浮体运动数值模拟设施的统称。它能够通过实验观测为各种波浪理论的研究奠定坚实的物理基础，还能为海洋、船舶等工程设计提供可靠而高效的试验数据。本文基于粘性流理论构建长峰波数值波浪水池，采用有限体积法 (FVM)对RANS方程和连续控制方程进行离散求解，利用Fluent软件的二次开发功能UDF，编写边界条件完成数值造波和阻尼消波功能。选用ITTC海浪谱作为目标海浪谱，构建长峰波数值波浪水池，并对其计算精度进行误差计算。

1.1 数值波浪水池的关键技术

1.1.1 数值造波

数值造波是指用数值方法模拟波浪的生成过程，为数值模型实验提供各种形式的波浪环境条件。本文采用的数值造波方法是边界条件造波法，即在数值波浪水池［1－2］入口边界设置3个方向的速度。X方向沿水池向下游为正，Z方向向上为正，Y轴与X轴和Z轴符合右手法则。3个方向的入射速度分别为:

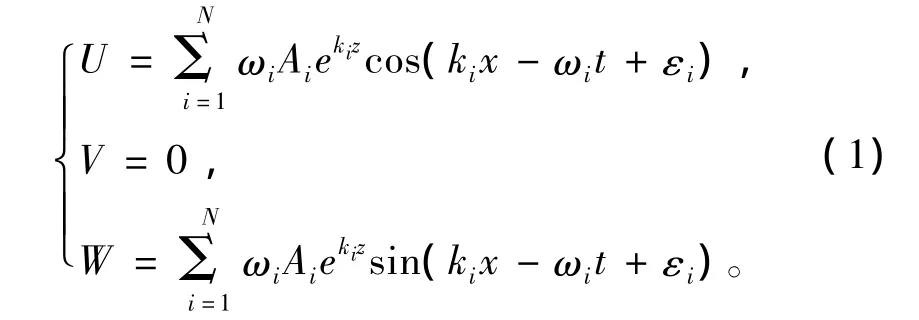
式中:η为波动水面相对于静止水面的瞬时高度;Ai，ki，ωi和εi分别为第i个组成波的波幅、波数、圆频率和初始相位，εi是在(0，2π)范围内的随机相位;X轴为波浪传播方向;U，V，W分别为波浪X轴、Y轴和Z轴的速度分量。

1.1.2 数值消波

当波浪到达水池末端开边界处，会引发水波的二次反射，反射波与入射波叠加，会导致波场的失真。因此，消除反射波的影响也是数值波浪水池的一项重要技术。数值波浪水池常用的消波技术主要有辐射边界条件消波、主动消波器消波、阻尼消波3种。本文选取的是阻尼消波。

阻尼消波法是指在流场中添加人工粘性，因其对来波的频率和波长不敏感，可以有效地消除各种频率和波长的来波，因而被广泛采用。在计算域出口边界前设置1～2倍波长的阻尼消波段，利用Fluent中的 UDF宏 DEFINE_SOURCE(mom_source，cell，thread，dS，eqn)编程实现消波。

在阻尼消波段内，动量方程写为:

其中μ(x)为在阻尼段起点为0的单调递增函数，可以取为线性递增、指数递增等形式。

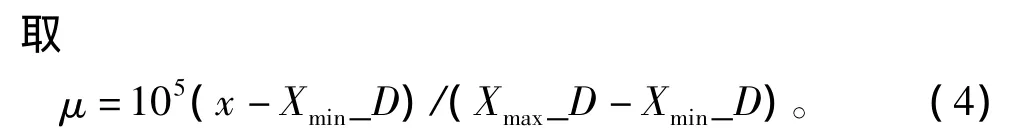
式中:Xmin_D和Xmax_D分别为消波区的最小、最大X坐标。

1.2 长峰不规则波数值波浪水池的构建

1.2.1 网格划分

三维数值水槽的网格划分如图1所示，本文构建的长峰不规则波数值水池［3－5］长18 m，其中12～18 m为消波区，宽3 m，深2.5 m，自由面以上1.5 m，整个水槽的网格数为413820。垂直自由面方向的网格尺寸取为有义波高1/5。造波区沿X轴正方向网格尺寸与垂直于自由面Z方向的最小网格尺寸相同，从自由面到水槽顶部网格按1∶1.1的比例等比分布;从自由面到水池底部网格按1∶1.05的比列等比分布。网格基本上是离自由面越远尺寸越大。对于消波区的网格划分，垂直方向划分与造波区的一致，水平方向网格以造波区网格尺度为基准向右边界逐渐扩大。

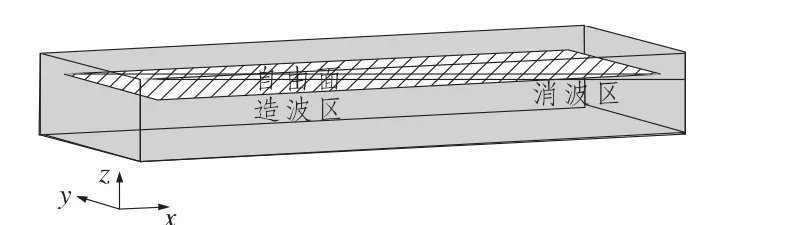
图1 数值波浪水池示意图Fig.1 Sketch map of the numerical wave tank

1.2.2 算例描述

选取ITTC海浪谱作为目标靶谱，对3种海况下的长峰不规则波进行数值模拟。波浪的目标参数见表1。

表1 ITTC海浪谱数值模拟参数Tab.1 Parameters for the simulation of ITTC wave spectrum

1.2.3 数值模拟结果

长峰不规则波数值模拟瞬时波面场和局部速度矢量如图2和图3所示。

图2 瞬时波面 (t=87.36 s)Fig.2 Instantaneous wave line

图3 局部速度矢量图Fig.3 Vectorgraph of partial speed

图4和图5是有义波高分别取H1/3=0.08 m，H1/3=0.125 m时，长峰不规则波数值波浪水池X=1 m，X=6 m，X=11 m处的波面时历曲线对比图。

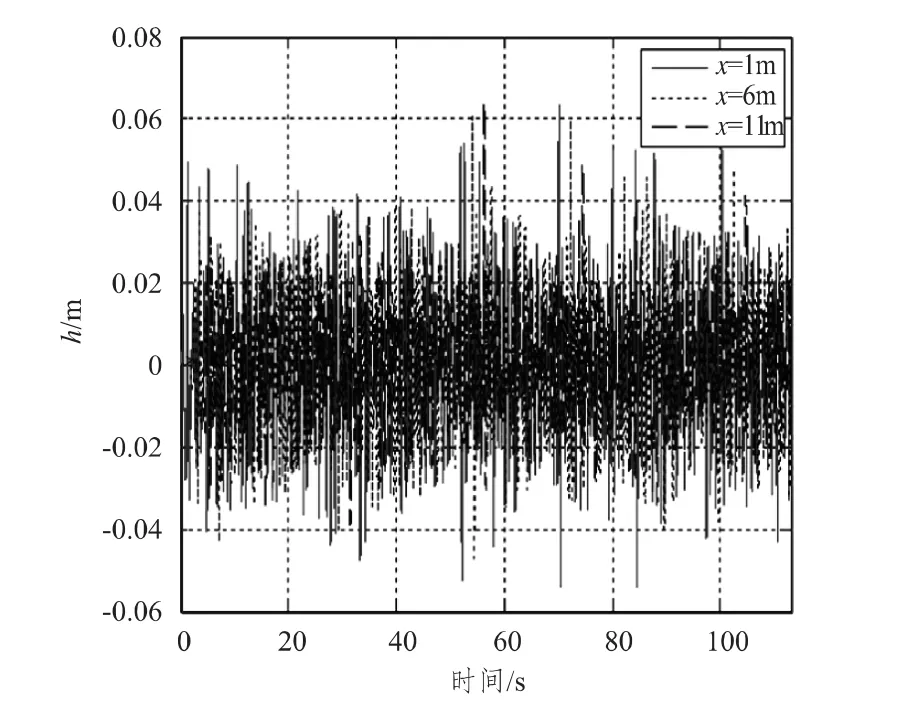
图4 时历曲线 (H1/3=0.08 m，Ts=1.092 s)Fig.4 Time history of wave line

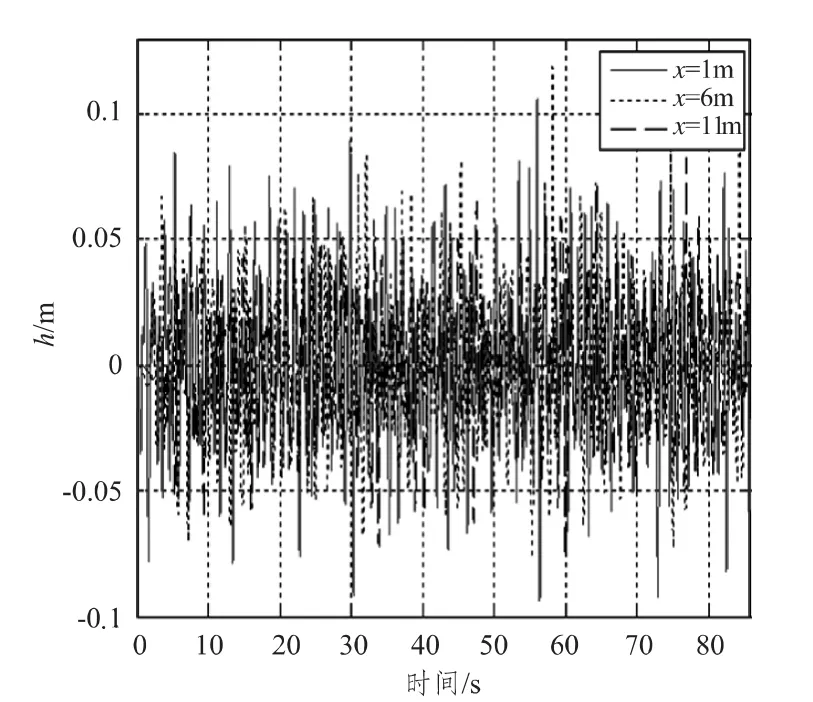
图5 时历曲线 (H1/3=0.125 m，Ts=1.365 s)Fig.5 Time history of wave line

从上述数值造波水池不同位置的波面时历曲线对比可看出，长峰不规则波在沿X轴正方向向下游传播过程中，波能有一定程度的衰减，这是由于波浪在传播过程中，高频子波衰减导致的。

1.2.4 数值模拟精度误差计算

对上面监测得到长峰不规则波波面时历进行谱分析与目标谱对比如图6所示。

图6 数值模拟海浪谱Fig.6 Numerical simulation spectrum

分别从谱面积 m0、谱峰频率 ωp和有义波高H1/33个方面对上述数值模拟海浪谱进行误差分析，误差计算结果如表2和表3所示。

表2 长峰不规则波相关误差计算 (ITTC谱X=1 m处波面时历)Tab.2 Relative errors for long-crested irregular waves

表3 长峰不规则波相关误差计算(ITTC谱X=6 m处波面时历)Tab.3 Relative errors for long-crested irregular waves

2 船模在长峰不规则波中顶浪纵向运动的数值模拟

2.1 船模的选择

选取具有球鼻首和方位的DTMB 5512船模作为研究对象，该船模是ITTC(国际船模试验水池会议)推荐的瘦削型标准船模DTMB 5415的全相似几何模型，以美国海军DDG－51型驱逐舰为模板，船型数据详实，而且与我海军舰船船型相似 (见图7)，适合军舰参考。表4为该船模及其所对应的实船尺度的主要数据。

图7 DTMB 5512船模Fig.7 Ship model of DTMB5512

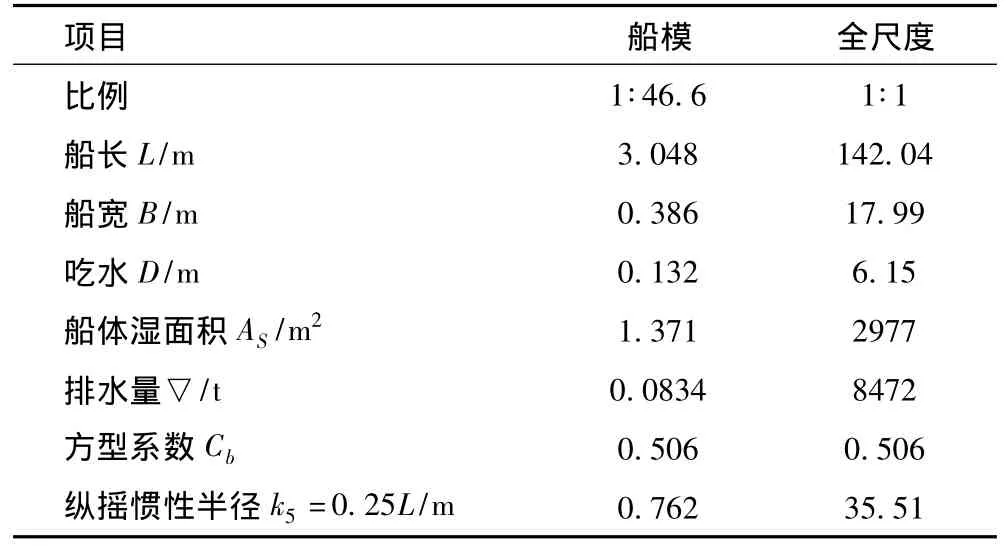
表4 船模和全尺度船的主要参数Tab.4 The primary parameter of DTMB5512 ship model

2.2 数值模拟方案

2.2.1 试验计划

本文对DTMB 5512船模在长峰不规则波中顶浪纵向运动数值模拟［6－8］试验中，只考虑垂荡和纵摇2个自由度的运动。船模CFD耐波性数值模拟试验对计算资源的要求较高，考虑到本文研究所使用的计算机配置的实际情况，以及试验水池网格划分所带来的计算效率等问题，试验计划如表5所示。

表5 DTMB 5512型船模顶浪纵向运动数值模拟试验Tab.5 Numerical simulation test of DTMB 5512 ship model

2.2.2 计算域划分

参照《水面船模耐波性实验规程》，将计算域设置成长方体形状，如图8所示。船模与计算域各边界的位置关系如下:入口距船首1倍船长，出口距船尾2倍船长，顶部边界距水线0.5倍船长，底部边界距水线1倍船长，左、右边界距船中纵剖面0.5倍船长。

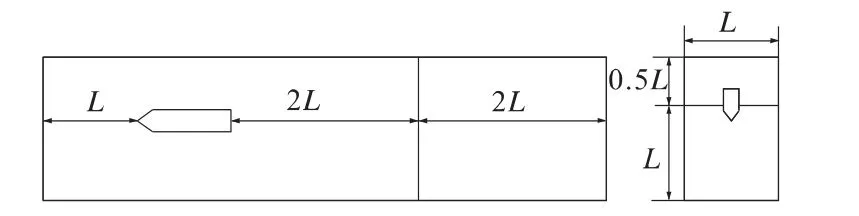
图8 水池计算域划分示意图Fig.8 Outline of computational domain for wave tank

耐波性数值波浪水池分成5个区域进行网格划分，即近船体区域、近流场区域、自由面区域、上下远流场区域及消波区域、各区之间互不重叠，且连接处选择connected方式，如图9所示。近船体区网格划分如图10所示。

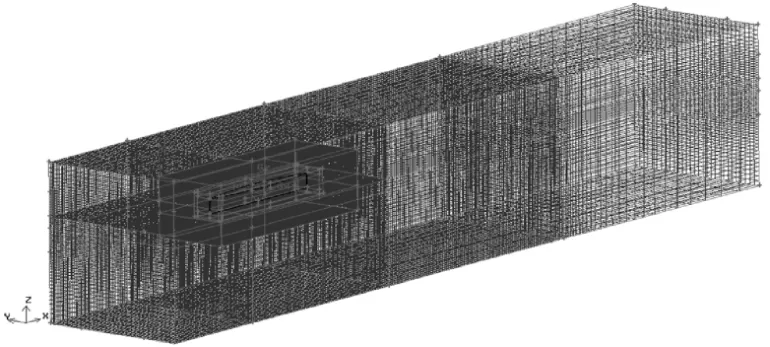
图9 耐波性波浪数值水池网格划分Fig.9 Build grid for sea-keeping numerical simulation wave tank

图10 DTMB 5512型船模近船体网格划分Fig.10 Build grid for the ship model of DTMB 5512

2.3 船模顶浪纵向运动数值模拟的求解过程

根据船舶六自由度运动的控制方程(5)，当波浪作用于船体时，其运动的速度、角速度以及位置、姿态等可以通过控制方程求解、积分得到。对于流浮耦合运动，波浪作用在船体上的力和力矩使船体产生运动，同时船体的运动又对其周围流场产生影响。因此本文在数值模拟中，分段计算流体与船体运动的耦合，步骤如下:

1)将船模按初始浮态固定，原点与重心重合;

2)对流场进行初始化，设定初始航速后造波;

3)以时间步长Δt=0.001 s步进;

4)通过当前流场变量迭代求解流场的速度矢量;

5)通过压力—速度耦合算法获得压力场;

6)求解体积分数方程重构自由面;

8)更新船体位置和浮态;

9)返回第3步，求解改变浮态后各量，并根据计算再次改变浮态，按此迭代求解，直到方程组的残差小于设定值或迭代次数达到设定值;

10)返回第2步并重复以下步骤，直到设定的时间步数计算完毕。

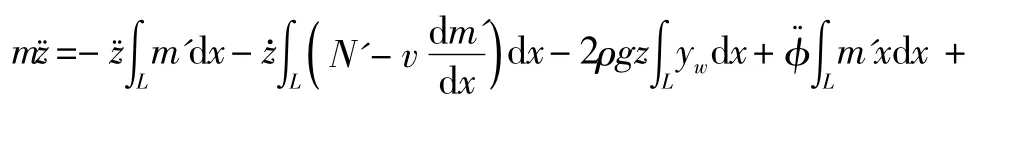
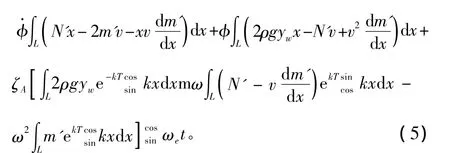
通过以上迭代、循环，可实现流体与船体运动的耦合。

步骤2按照1.2节构建的数值波浪水池进行造波和消波。试验过程中可以将事先保存好的稳定流场导入耐波性数值模拟水池，进行数值模拟，这样可以提高计算效率，缩短试验时间。步骤4～6，按前文设置的数值方法进行计算。步骤7则通过UDF编程实现。步骤9残差标准可取软件默认设定值，迭代次数上限为40步。

2.4 数值模拟结果

对于DTMB 5512船模由于带球鼻首、具有方尾，线性复杂，所以实现其耐波性的数值模拟，要比一般商用船模困难得多。可采用以下方法对实验进行改进:

1)改进船模贴体网格质量、数量及分区网格的匹配;

2)采用递增方法实现船模的纵向运动，即先对船模进行单自由度纵摇，稳定之后再增加垂荡的数值模拟;

3)逐渐增加船模质量 (将船模质量降低到原船模的一半进行数值模拟，当残差稳定后再逐渐增大质量直至原值);

4)减小欠松弛因子，控制单元网格内速度的变化量。

通过上述方法，解决了DTMB 5512船模复杂的几何船形与波浪作用的数值问题。

DTMB 5512型船模在长峰不规则波中纵向运动数值模拟的压力场和速度场，如图11和图12所示。

图12 DTMB 5512船模数值模拟速度场Fig.12 Numerical simulation speed field for the ship model of DTMB 5512

DTMB 5512型船模在长峰不规则波中纵摇及垂荡的时历曲线如图13和图14所示。

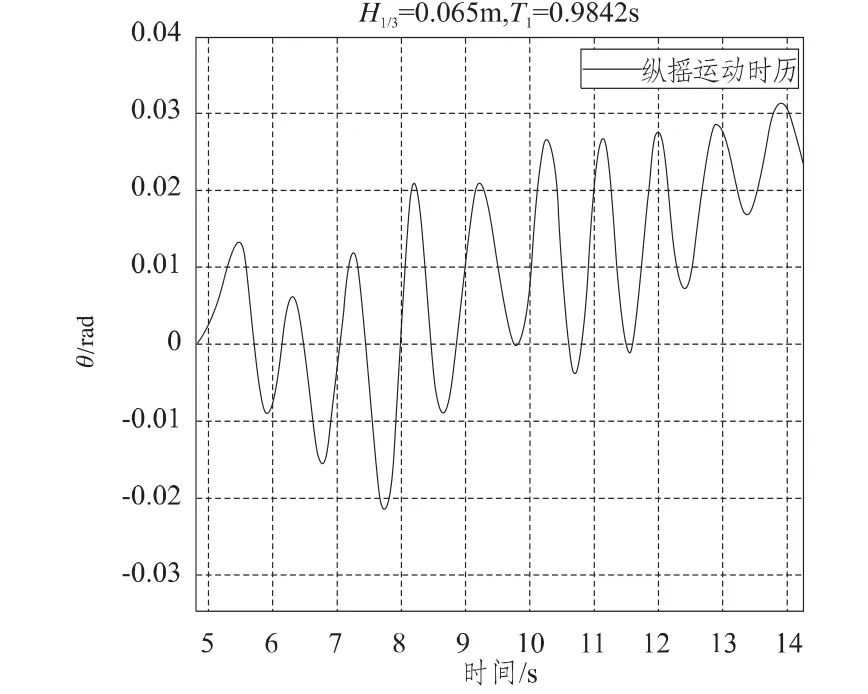
图13 纵摇运动时历曲线Fig.13 Time history of pitch movement

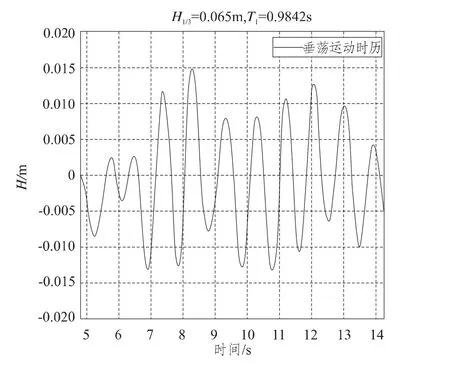
图14 垂荡运动时历曲线Fig.14 Time history of heave movement

3 数值模拟结果验证

由于本文对船模在长峰不规则波中顶浪纵向运动的数值模拟研究目前在国内外还处于起步阶段，未找到具体的水池实验数据。考虑到基于势流理论舰船六自由度计算，在理论上是成熟的，并在工程应用上取得了很多成果，得到了水动力学界认可。一般来说，SCFD方法由于考虑到流体粘性，计算精度应略高于势流理论计算结果，但没有本质上的差异。至于非线性摇荡则需要另作考虑，本课题局限于线性摇荡，所以用势流理论计算结果进行验证［9］是可行的。

由于势流理论切片法计算过程相对繁琐，可参考文献［1］，本文直接给出DTMB 5512型船模在算例波浪环境下纵摇和垂荡的响应方差。

将数值模拟的DTMB 5512型船模摇荡运动时历曲线运用线性谱分析方法进行分析，获得纵摇及垂荡的摇荡谱，如图15和图16所示。

图15 纵摇运动响应谱Fig.15 Responsive spectrum for pitch movement

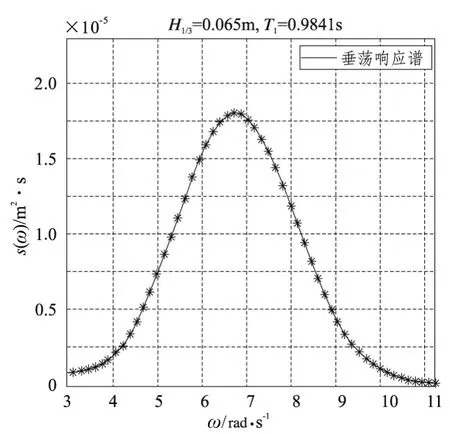
图16 垂荡运动响应谱Fig.16 Responsive spectrum for heave movement

对上述摇荡谱进行积分即可得到本文数值模拟DTMB 5512船模顶浪运动纵摇和垂荡的响应方差。

对DTMB 5512型船模在长峰不规则波中顶浪纵向运动的数值结果与势流理论计算结果进行对比得出相对误差如表6所示。

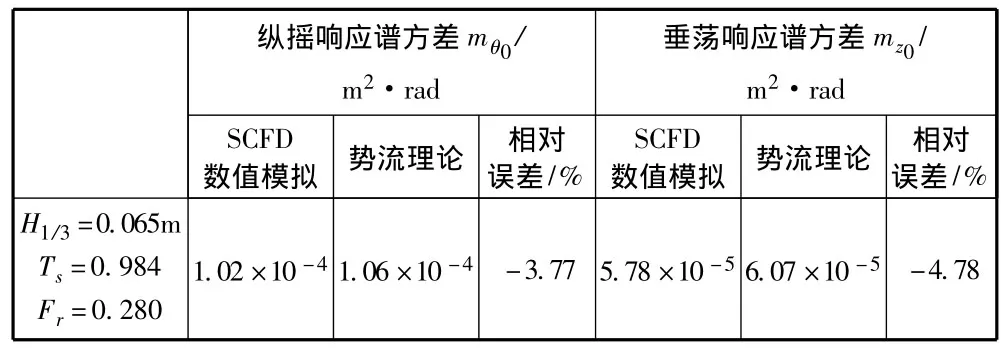
表6 DTMB 5512型船模相对误差计算Tab.6 Relative errors for the ship model of DTMB 5512

4 结语

本文运用SCFD方法对舰船在长峰不规则波中顶浪运动进行数值模拟，得到如下可供参考的经验:

1)船舶摇荡、阻力、操纵、推进等课题的数值研究，技术细节上的一个主要不同，体现为网格的布设上。

2)船舶耐波性研究的网格，必须将造波和船体网格、动网格三者进行很好的协调、匹配，做到三者的有机结合，否则会出现计算发散及非物理现象等不合理现象的发生。

3)船舶多自由度摇荡试验目前的困难主要集中在计算资源上，由于其计算量巨大，PC机以及低端的工作站、服务器已经不能满足其正常情况下的计算需要。如果计算资源等硬件设施有限，则需要在离散方法、格式，控制方程、调节参数、UDF开发等“软件”上下功夫。

4)在三维空间内完成船模非规则波中的摇荡试验，其流场及自由面要比船模在规则波中的复杂得多，因此在船模贴体网格的布设上，要求网格质量非常高，同时在interface交界面处，左右网格要尺寸一致，且在船模外表面尽可能多地使用结构性网格，特别是在阻力计算上，还要尽可能多地布设边界层，以提高计算的精度。

5)耐波性流场的高度复杂性还表现在输入、输出及船模的响应及其变化率上。具体表现为1个网格上，至少要输入3个方向的线速度 u，v，ω，压力P，参数k，ε，流体体积分数Cq等7个参数，及其输出 u'，v'，ω'，P'，k'，ε'，C'q，并且要求它们之间的时空变化率在一定的范围内。

6)船模外形的复杂程度也对船模多自由度摇荡试验产生一定的影响，当计算资源无法满足大计算量的计算时，应尽量考虑用外形简单、对称性好的船模，如Wigley系列船模，以防止计算发散及非物理等不合理现象的发生。

7)耐波性波浪数值水池的网格布设同船模摇荡的维数密切相关，而且同等条件下，在傅汝德数适中的情况下，计算效果较好。

8)在波浪的选择及其他相关参数的选择上，尽量参照《耐波性试验章程》的相关要求，以防止非物理等不合理现象的发生。

［1］吴乘胜，朱德祥，顾民.数值波浪水池及顶浪中船舶水动力计算［J］.船舶力学，2008，12(2):168 －179.WU Cheng-sheng，ZHU De-xiang，GU Min.Computation of hydrodynamic forces for a ship in regular heading waves by a viscous wave tank［J］.Journal of Ship Mechanics，2008，12(2):168－179.

［2］董志，詹杰民.基于VOF方法的数值波浪水池及造波、消波方法研究［J］.水动力学研究与进展(A辑)，2009，24(1):15－21.DONG Zhi，ZHAN Jie-min.Comparison of existing methods for wave generating and absorbing in VOF-based numerical tank［J］.Journal of Hydrodynamics，2009，24(1):15 －21.

［3］GRILLI S T，VOGELMANN S，WATTS P.Development of a 3D numerical wave tank for modeling tsunami generation by underwater landslides［J］.Eng Analwith Boundary Elements，2002，26:301 －313.

［4］ARAI M，PAUL U K，CHENG L Y，et al.A technique for boundary treatment in numerical wave tanks［J］.Journal of the Society of Naval Architects of Japan，1993.

［5］吴乘胜，朱德祥，顾民.数值波浪水池中船舶顶浪运动数值模拟研究［J］.船舶力学，2008，12(5):692 －696.WU Cheng-sheng，ZHU De-xiang，GU Min.N-S CFD simulation of wave-induced ship motions in regular head waves［J］.Journal of Ship Mechanics，2008，12(5):692 －696.

［6］郭海强，朱仁传，缪国平，余建伟.数值波浪水池中船舶水动力系数测试与分析技术［J］.中国造船，2008，49(S):58－65.

［7］RICCARDO B，ADREA D M.Unsteady RANS calculation of the flow around a moving ship hull［C］.In:Proc.of 8th International Conference in Numerical Ship Hydrodynamics，Busan:2003，A:153 －165.

［8］LUQUET R，JACQUIN E，GUILLERM P E，GENTZ L，et al.RANSE with free surface computations around fixed and free DTMB 5415 model in still water and in waves.Proc.the CFD Workshop Tokyo，2005.

［9］李积德.船舶耐波性［M］.哈尔滨:哈尔滨工程大学出版社，1992:1－10.