圆环形仿形机织物的剪切变形

陈和春， 陈桂香

(南通纺织职业技术学院 纺织系， 江苏 南通 226007)



圆环形仿形机织物的剪切变形

陈和春， 陈桂香

(南通纺织职业技术学院 纺织系， 江苏 南通 226007)

仿形织物织造过程中，由于使用的是异型卷取轴，纬纱在卷取时发生变形，形成剪切角，使得仿形织物上机前后在结构上产生较大的差异。为此，针对采用锥形卷取辊织造圆环形仿形织物产生的纬向剪切变形问题，分析了织物在织造、卷取时的结构特点，建立圆环形仿形织物的剪切变形模型，推导理论变形公式，计算出圆环形仿形织物的纬向剪切角，并将理论计算的剪切角与实测的剪切变形角进行对比，发现二者非常接近。证明该理论推导公式是正确的，符合织物剪切的实际情况。

仿形机织物； 剪切变形； 理论模型； 剪切角

复合材料领域中应用最为广泛的增强材料主要是平面结构的机织布，但由于玻璃纤维和碳纤维弹性差，因此在织造曲面形状的复合材料时，一般需要将二维平面织物进行剪裁，然后将开剪的织物通过黏贴等方法制成复合材料预制件[1]。这种方法仍存在诸多不足：首先开剪织物增加了成型工艺，使得工艺复杂化；其次，由于织物在预制件内部并非连续，肯定将影响复合材料的力学性能；再次，剪裁工艺也不利于复合材料的规模化、连续化生产，因此，针对平面织物制作复合材料的不足，许家忠等[2-3]提出了曲面机织布的仿形生产技术。

仿形织造技术是根据复合材料制品的几何形状，在普通织机上进行部分机构的改进来生产单层仿形机织物[4-5]。仿形织造技术所生产的织物一般都是以回转体外形来设计织物，所织的织物以经纬纱不等长[6-7]为特点，具有空间曲面机构，应用时只需将织物进行多层卷绕即可获得所设计的回转体形的复合材料制品形状[8]，但在织造设计过程中发现，最后成品形状与所设计的尺寸之间有很大差异。本文根据圆环形仿形织物织造过程中的纱线变形，通过理论推导计算，将织造中的变形用公式表示，这样有助于所设计的仿形织物更加符合设计要求，为该类织物的设计提供参考。

1 圆环形仿形织物剪切变形的原因

圆环形仿形织物是将普通有梭织机的圆柱形卷取辊改成圆锥台，如图1所示，并在织物组织上配置不等长的纬纱而形成的。由于圆锥台形卷取辊的截面圆的直径不同，导致在相同的卷取角速度的条件下，卷取辊表面纵向的线速度不同，截面圆直径大的其线速度高，直径小的线速度低，使卷取辊直径大的地方需要的经纱长，而在卷取辊直径小的部分需要的经纱长度相应的要偏短。但是，不管是对卷取辊直径大的部分还是直径小的一端，从织口到织物卷入卷取辊间的距离都是一样的。卷取辊沿轴向表面线速度不同，卷取辊直径大的部分织物被卷入的速度快，卷取辊直径小的部分织物被卷入速度慢，使得织物内的纬纱不能以平行于卷取辊轴的形式卷入卷取辊，从而导致圆环形织物的纬纱与经纱产生剪切现象[9]。

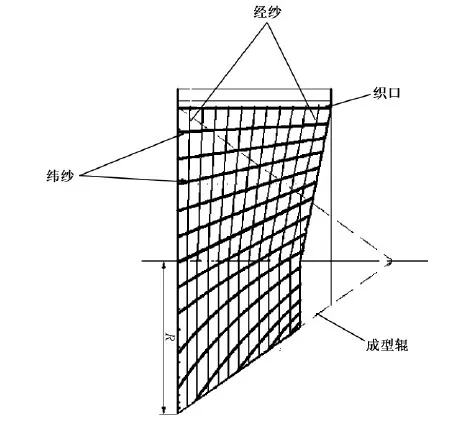
图1 圆环仿形织物上机织造图Fig.1 Sketch of annular shape fabric on frame

2 圆环形织物剪切模型的建立

根据织物织造过程中的变形情况，设计出圆环形仿形织造织物的变形示意图，如图2所示。

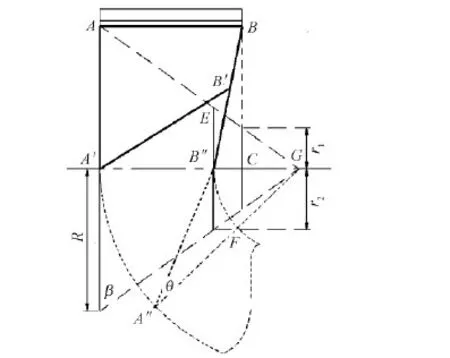
图2 圆环仿形织物在机变形示意图Fig.2 Sketch of shear deformation of annular shaped fabric on frame

设圆锥台底部半径为R，上端直径为r1，织物卷绕后的上端半径(B″C)为r2，圆锥台的底角为β。AB为织物的织口，AB平行于卷取辊轴，所有的纬纱都在AB处以前后平行的方式织入织物；直线A′C为圆锥形成型卷取辊表面上的1条母线，织物将从A′C处被卷取，紧密地缠绕在成型卷取辊上，所以A′C为织物的卷取起始线。设织物织口AB与织物卷取起始线A′C之间的距离为l1。

图2演示的为织物的卷取过程，当1根纬纱在AB处织入织物，由于卷取辊沿轴向各点线速度不同，当纬纱处于直径大的一端(即图2中A点)到达卷取起始线(如图2中A′点)时，该纬纱处于卷取辊直径小的一端(即图2中B)才到达B′，设此时成型卷取辊转动的角度为α，则有：

(1)

而当该纬纱处于卷取辊直径小的一端也以缓慢的速度达到卷取起始线(如图2中B″)时，该根纬纱的另一端早已卷入卷取辊到达A″点的位置了，因此，在织物织口AB处织入的纬纱上的各点没有同时进入卷取起始线，如果不发生剪切， 当A点到达A″点的位置时，B点到达F点的位置，但是现在当A点到达A″点的位置时，B点却只能到达B″点的位置，所以产生了剪切，设剪切角为θ。将卷在成型卷取辊上的织物展开，如图3所示。

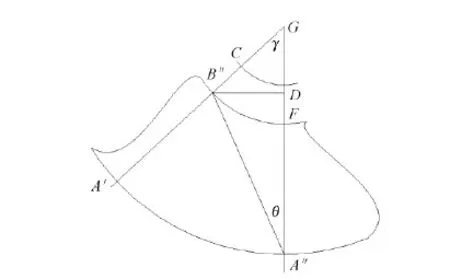
图3 仿形织物展开示意图Fig.3 Sketch for expandness of annular shape fabric

A′A″所对应的织物展开平面的圆弧角为γ，作B″D垂至A″G于点D。

图2中三角形BB″C为直角三角形，根据直角三角形勾股定理，则有：

(2)

将各个参数代入，有

(3)

图3中的三角形A″B″D为直角三角形，根据勾股定理有

(4)

将参数代入整理得：

(5)

由式(3)、(5)联立方程组，得：

(6)

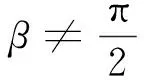
(7)

3 剪切理论公式的计算与实验验证

把R=45 mm,r1=15 mm,β=π/4,l1=45 mm代入方程组(7)，得：

(8)

简化为：

(9)

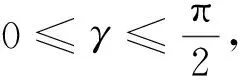
(10)

且15≤r2≤45，0≤γ≤0. 729 7。

通过MatLab[10]，作方程组的求解图，见图4。

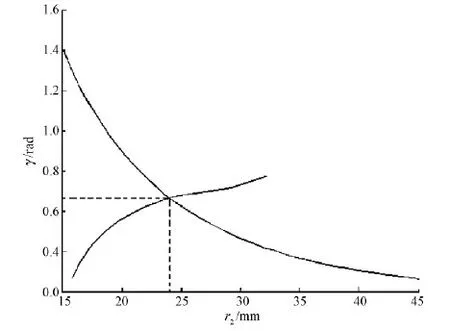
图4 方程组的MatLab求解图Fig.4 Sketch of MatLab solving to equations

从图4可得方程组的近似解：

(11)

则此时图3中圆环形织物在展开平面上的剪切角

将方程组解式(11)代入式(13)，得:

将式(14)、(15)代入式(12)，得：

(16)

即在R=45 mm,r1=15 mm,β=π/4,l1=45 mm条件下，织物的在机剪切角θ≈29.67°

在实际的织造过程中，采用了底部圆直径为90mm，圆锥底角为45°,高为30mm的正圆锥台作为卷取辊，并且采用了二上二下斜纹组织，织口与织物在卷取辊上卷曲起始线间距离为45mm，即织造的参数满足R=45 mm,r1=15 mm,β=π/4,l1=45 mm。仿形织物完全卷入卷取辊后，取15个不同的位置测量纬纱剪切角度，取平均值为33.7°。

4 结 论

1)基于在普通有梭织机上面采用圆锥台形的成型卷取辊，详细分析织物从织口到完全卷入卷取辊间的运动过程及纬纱产生剪切的原因，建立了纬纱剪切的模型。

2)在建立的模型中共有6个变量，根据模型特征，推导出6个变量的方程组；若该方程组中6个变量中的任意4个变量为已知条件，则该方程组即变成1个二元方程组，可对方程组进行求解，确定2个变量,因此该理论公式可为回转体形的仿形织物的上机参数、复合材料件与成型卷取辊的结构参数间的关系提供一种计算方法。

3)在R=45 mm,r1=15 mm,β=π/4,l1=45 mm的条件下，使用MatLab软件对方程组求解，得出γ≈0. 66 rad,r2≈24.2 mm，最后计算得出在此条件下圆环形仿形织物纬向的剪切角θ理≈29.67°。

4)在实际织造的情况中，织物采用的是二上二下斜纹组织，实际测得的织物纬向剪切角为θ理≈33.7°。实际测得的剪切角略大于理论计算出的剪切变形角，但二者非常接近，证明建立的理论模型和理论推导基本符合实际情况，是正确的。

FZXB

[1] 郭兴峰, 刘春阳, 王瑞,等. 圆环形织物的织造原理与设计[J].纺织学报，2006，27(1)，12-15.GUOXingfeng,LIUChunyang,WANGRui,etal.Weavingprincipleanddesignoftheannularshapedwovenfabrics[J].JournalofTextileResearch, 2006，27(1)，12-15.

[2] 许家忠，乔明，尤波,等. 纤维缠绕复合材料壳体原位成型工艺研究[J].材料科学与工艺,2009(12):191-194.XUJiazhong,QIAOMing,YOUBo,etal.Theresearchofin-situmodelingprocessforfiberwindingcompositeshell[J].MaterialsScience&Technology, 2009(2):191-194.

[3] 彭淑静，郭兴峰.单层曲面机织布的织造技术研究[J].纺织科技进展，2005,26(2)：18-20.PENGShujing,GUOXingfeng.Theweavingtechnologyofmonolayercamberweaving[J].ProgressinTextileScience&Technology, 2005,26(2)：18-20.

[4] 郝志坚，郭兴峰.锥形管状预成型机织物的织造方法研究[J].产业纺织品，2005，23(12)：23-25.HAOZhijian,GUOXingfeng.Studyontheweavingmethodsofcone-shapedtubularwovenpreforms[J].IndustrialTextile, 2005，23(12)：23-25.

[5] 郭兴峰, 李济群. 一种机织物的织造方法：中国,CN02129080.6[P].2005-03-12.GUOXingfeng,LIJiqun.Amethodforwovenfabrics:China,CN02129080.6[P]. 2005-03-12.

[6]BUSGENA.Gewebteformen-standundausblickneuerwebtechnologien[J].MelliandTextilberichte, 1999(6):502-505.

[7]ROBERTGJamesH,MICHEALH.Compositeoverwrappedpressurevesselsforspaceapplications[J].SampeJournal, 2003, 39(2):44-50.

[8] 彭淑静, 郭兴峰, 陈和春. 圆环形机织布的织造与设计[J]. 天津工业大学学报，2005，22(4)：18-20.PENGShujing,GUOXingfeng,CHENHechun.Designandweavingofannularcloth[J].JournalofTianjinPolytechnicUniversity, 2005，22(4)：18-20.

[9] 陈靖芯,徐晶, 李红,等. 曲面展开技术的研究及其应用[J]. 扬州大学学报：自然科学版， 2003， 6(3)：54-70.CHENJingxin,XUJing,LIHong，etal.Researchofsurfacedevelopingtechnologyandapplication[J].JournalofYangzhouUniversity:NaturalScienceEidition, 2003，6(3)：54-70.

[10] 李丽,王振领.MatLab工程计算及应用[M].北京：人民邮电出版社，2001: 162-165.LILi,WANGZhenling.MatLabEngineeringCalculationandApplication[M].Beijing:Post&TelecomPress, 2001: 162-165.

Shear deformation of annular shaped woven fabrics

CHEN Hechun， CHEN Guixiang

(TextileDepartment,NantongTextileVocationalTechnologyCollege,Nantong,Jiangsu226007,China)

For weaving shaped fabrics, the batch roller on shape weaving frame is of cone frustum, not cylinder, which makes the shear deformation happen when copping, thus forming a shear angle so that the structure of the shaped fabric differs remarkably before and after looming. This paper, aiming at solving the weft shear deformation problem which exists in annular shaped fabric′s weaving, analyzes the structural characteristics of the annular shaped fabric when weaving and winding, establishes a shear deformation model of the annular shaped woven fabric, derives a theoretical shear deformation formula, and calculates the weft-wise shear angle of the fabric. The comparison between the calculated shear angle and the measured one demonstrates that the two are very close. This proves the derived theoretical formula is correct and accords with the actual situation of the shear deformation.

shape woven fabric； shear deformation； theoretical model； shear angle

0253- 9721(2013)04- 0053- 04

2012-04-23

2012-10-22

陈和春(1979—)，男，讲师， 硕士。主要研究方向为仿形机织物的织造和功能纺织品研发。 E-mail:yacht_103@163.com。

TS 101.1

A