集装箱堆场作业优化模型与算法

赵艳艳

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

吊车频繁进行装卸与倒箱作业，不但浪费时间，增加劳动强度，制造噪音污染，而且对集装箱及其内部装运货物造成一定的损害，因此，如何规划龙门吊的作业顺序，减少作业次数成为衡量堆场工作效率的关键。

江南学者建立铁路集装箱堆场作业静态码垛模型和动态码垛模型，并设计箱小区判定算法和单箱码箱取箱算法，同时建立循环码垛模型，并设计循环单箱码箱算法、构造动态全序算法和暂扣标记设置解除算法。李建忠建立一个多目标非线性数学规划模型，以各箱区总的未按计划完成工作箱量所需的龙门起重机时间和龙门起重机闲置时间的最小化为优化目标，从而解决轮胎式龙门起重机的动态优化配置问题。

由于发站集装箱吊车作业与到站集装箱吊车作业过程相同，只是顺序相反；对于堆场来说，要先卸车后装车，所以，只需增加相应的作业变量即可按相同方法处理。

1 建立模型

1.1 假设条件与说明

本文提出假设：

1）集装箱同时到达堆场等待卸车，但离开时间是随机的，且从到达之日起集装箱只能在堆场停留3d。

2）与提箱作业和卸车作业时间相比，吊车行走时间较短、技术要求也不高，所以，忽略不计行走时间。

3）吊车实际作业顺序，当货主停车进行提箱作业时，集装箱到达并有停车空位时进行卸车作业，即混合进行作业，这样使作业高度不确定。因此，假设吊车按先卸车后提箱顺序进行作业，只考虑卸车时集装箱堆码顺序，使提箱时倒箱作业次数最少。

4）每个箱位只能堆放两层。

5）计划期为3d，每天为一个阶段。

1.2 参数说明与决策变量设置

每个集装箱有唯一编号对应，令i（i∈M）为集装箱编号，M为集装箱编号集合。为使问题处理方便，可按集装箱到达先后顺序将M映射到自然数子集I中，同一阶段到达的集装箱按其编号由小到大排序，即i∈I＝｛1，2，…，m｝。j为箱位，j∈J＝｛1，2，…，n｝；n为货场最大箱位数；k为某箱位堆放的集装箱层数，k∈K＝｛1，2，…，s｝，s为堆放最高层数；ξi为集装箱i的离开时间。

定义集装箱卸车作业变量为

1.3 约束条件

兰州市北货场受场地限制，每个存装区只有3排箱位供存放集装箱，每排有49个箱位。由于受到龙门吊高度的影响，每个箱位只能堆放2层。

卸车作业需满足约束条件为

每个集装箱只能放在一个位置

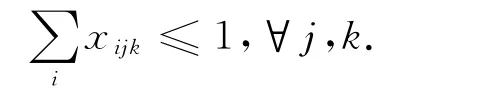
每个位置最多放一个集装箱

位于j箱位第1层的集装箱i1的提箱时间迟于位于j箱位第2层的集装箱i2的提箱时间的概率，且应不小于常数α。

提箱时倒箱作业约束为

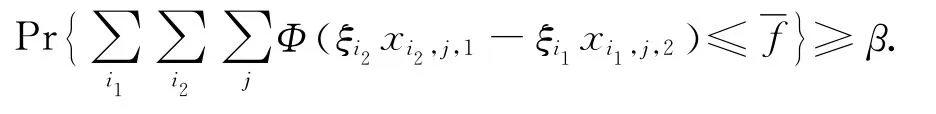
当j位上下层都有箱，且下层提箱时间早于上层提箱时间时，需进行倒箱作业，且倒箱作业的次数不大于的概率，且不小于常数β概率；其中Φ（x）为符号函数：

1.4 目标函数

目标函数为总倒箱次数最小

2 算法设计

2.1 编码表示

染色体Y的表示见图1。

图1 染色体的表示方法

分别对箱位j，层数k和k′进行整数编码，建立基因组（ji，ki，k′i）；其中ji，ki为第i个集装箱位于ji箱位ki层；k′i为i个集装箱，如需要倒箱则倒箱后位于ji箱位k′i层。染色体的长度为到达集装箱数量3倍。

2.2 解 码

对基因组（ji，ki，k′i），显然xijk＝1。当ki＝k′i时，该箱不需要倒箱；当ki＝2，k′i＝1时，该箱需被倒箱一次。

2.3 适应度函数

模型含有大量约束条件，计算过程进行可行性验证将耗费大量时间，采用罚函数法将其转变为无约束优化问题，对于下面的约束问题优化

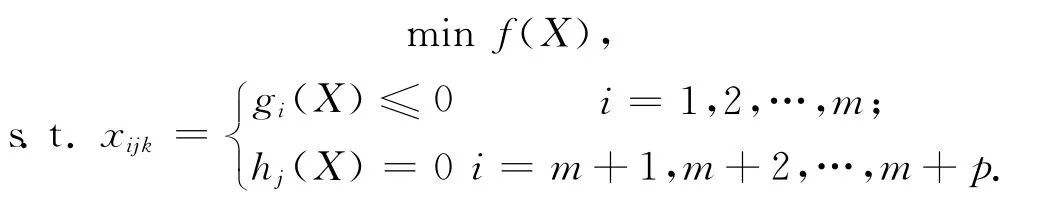
可转化为无约束优化问题

式中：MT为罚因子向量；Q（X）＝ （Q1（X），Q2（X），…，QM＋P）为罚函数向量，Qi（X）定义为

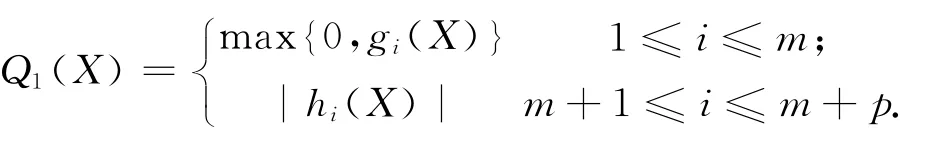
适应度函数为

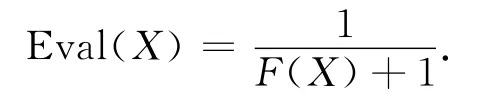
2.4 交叉与变异

采用两点交叉，首先按交叉概率pc选择父代染色体，随机产生n1和n2∈[1，n]，且n1≠n2，对任意两个父代染色体Vti和Vtj，保留前n1－1和后nn2＋1位基因组不变，变换n1位到n2－1位的基因组，形成两个子代染色体Vt＋1i和Vt＋1j。例如：n＝7，n1＝3，n2＝5；其交叉操作见图2。

图2 两点交叉操作

采用逆转变异：对每个染色体，当随机数小于变异概率pm时，随机产生两个整数n3和n4∈[1，n]，且n3≠n4将两个整数内基因组按逆序插入到原位置中，见图3。

逆转变异：

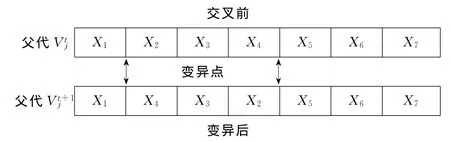
图3 逆转变异操作

2.5 算法的步骤

步骤1输入参数pop－size：pc及pm；

步骤2初始产生pop－size个染色体，其中可能使用随机模拟技术检验染色体的可行性；

步骤3对染色体进行交叉和变异操作，其中可能使用随机模拟技术检验后代的可行性；

步骤4使用随机模拟技术计算所有染色体的目标值；

步骤5根据目标值，使用基于序的评价函数计算每个染色体的适应度；

步骤6旋转赌轮，选择染色体；

步骤7重复步骤2到步骤5，直到完成给定的循环次数；

步骤8给出最好的染色体作为最优解。

3 算 例

3.1 初始条件

为了说明模型的实用性和程序的可行性，简化实际的集装箱场：

1）箱场区初始为空；

2）集装箱场区内用于卸集装箱的箱位有6个，编号为：Bay1、Bay2、Bay3、Bay4、Bay5、Bay6集装箱堆码为两层，如图4所示；

3）集装箱到达等待卸车区域，到达的集装箱都在3个阶段内离开，离开时间不确定，在每一阶段离开概率随即产生；

4）初始到达集装箱数量固定为范0个；

5）假设α和β均为0.6；

6）用C＋＋编写程序及得出的结果如表1所示。

图4 箱场区初始为空的示意

3.2 程序运行结果及说明

在给定的初始条件下，在3d计划期内，合理地安排集装箱的堆码位置可以使得集装箱装卸机械在整个装卸作业过程中不产生倒箱作业。这不仅提高了装卸机械的作业效率，同时也减轻倒箱作业过程中对箱体的损害和对集装箱内货物的货损。最优结果如表1所示。

表1 最优结果

4 结束语

通过对集装箱箱场区作业的分析和总结，到达重集装箱卸箱次数为例，建立了箱场区初始阶段为空的模型。通过减少龙门吊的作业次数，有效地优化堆场内零散箱的箱位分配，提高集装箱堆场的作业效率。

[1] 段钢，陈莉.铁路集装箱堆场混堆区箱位分配优化模型与算法[J].铁道学报，2011，33（7）：32－36.

[2] 江南，钱迈.集装箱堆场作业计划模型及算法[J].铁道学报，2009，31（5）：9－15.

[3] 李建忠，韩晓龙.集装箱港口堆场轮胎式龙门起重机的动态优化配置[J].上海海事大学学报，2005，26（3）：44－48.

[4] 陶经辉.基于混堆模式的集装箱堆场区段分配[J].系统工程理论与实践，2009，29（8）：185－192.

[5] 王志明，符云清.基于遗传算法的集装箱后方堆场箱位分配策略[J].计算机应用研究，2010（8）：66－68.

[6] 丁香乾，韩运实，张晓丽.自适应遗传算法解决集装箱装载问题的方法探讨[J].中国海洋大学学报，2004，3（5）：844－848.

[7] 谭浩强.C＋＋程序设计[M].北京：清华大学出版社，2004.