铁路物流中心功能区布局方法分析
韩 琨
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
1 研究现状
我国的物流业起步较晚,在物流中心内部的布局问题上更是没有像发达国家那样有较多的经验可供借鉴。在国外,解决布局问题的方法具有较长的历史,从最传统的图解法到数学模型法、计算机辅助设计方法以及系统布置规划法(Systematic Layout Planning,SLP)等。在这众多的方法当中,SLP方法以其能充分考虑定性因素和定量因素的优点而多被采用。由于求解布局问题是非线性的NP难题,目前,多用于求解的方法有启发式算法、智能算法(遗传算法、模拟退火算法,蚁群算法等)、计算机模拟等。
在充分考虑特路物流中心特点及功能的条件下,本文采用改进SLP方法解决功能区布局问题。首先,应用现有资料分析物流园区内各功能区之间的综合关系;其次,以各功能区之间相互关系最大和整个物流中心成本最优两个目标建立数学模型;最后,采用遗传算法求解该模型,得出最优布局方案。
2 布局方法
2.1 铁路物流中心功能区的划分
物流中心作为一种专业化的物流组织,不仅需要具备一般的物流服务功能,还应该具备提供适合不同需要的高附加值和定制化服务的增值功能。因此,一般的物流中心功能区都分为物流功能区和非物流功能区两大类。在铁路物流中心,更是应该把铁路作为影响物流功能区的主要因素考虑进去。通过分析铁路物流中心的作业流程及各项作业的特点,可将物流功能区和非物流功能区更细致的划分为10个功能区。
2.1.1 物流功能区的划分
分析物流中心内相关的物流作业项目、物流作业流程与物流中心功能的关系以及物流活动之间的关系,我们可将物流功能区分为理货区、流通加工区、仓储区、退货区。
1)理货区。主要承担理货、点货、拣货、分类、集货、验货、配货等职能。该功能区负责进行货物到达物流中心进入后续流程的前期处理和货物即将从物流中心出去之前的前期处理工作。
2)流通加工区。主要承担对一些初级产品的二次加工、零配件组装为成品的加工作业,以及产品包转、运输包装、流通包装打印条码等职能。
3)仓储区。主要承担货物的仓储保管的职能。根据货物的种类、运输形式及存储条件,可将仓储区细分为普通仓库、特殊仓库(包括鲜活货物、立体仓库、保税仓库等)、集装箱堆放场、散货堆场及长达笨重货物堆放区等。
4)逆向物流作业区。主要承担对退货、瑕疵品及废品进行处理的职能。可以细分为退货退货卸货区、退货处理区、换货区、瑕疵品暂存区等。
2.1.2 非物流功能区
物流中心除了是货物的集散中心外,还是客户的交易中心。故物流中心还应该为客户提供产品的展示、卡车停放、商检、金融保险等各种增值功能的服务。
1)交易展示区。主要是为供需双方提供产品交易和展示的平台,并且可以随时更新市场供求信息。
2)停车场。主要用于配送货物的车辆停靠。利用即时信息功能,为货主和货车司机提供运输供需的信息。
3)管理办公区。主要为物流中心的行政办公、业务办理和招商引资的区域。本功能区提供物流调度和物流咨询,以及一关三检、工商、海关、税收、银行和保险等配套业务。
4)生活服务区。主要是为客户及物流中心工作人员提供休息和餐饮的区块。同时,可以对外提供车辆的加油、维修等服务。
5)虚拟功能区。主要是针对连接物流中心内部与外部的交通方式及设备建立的虚拟区块。其主要包括铁路装卸线和物流中心出入口等。
2.2 系统布置设计(SLP)方法
1961年,Richard Muther提出了SLP方法,此方法最早应用于工厂设计布置当中,使得工厂布置从定性阶段发展到到了定量阶段。在后期的物流中心布置当中,SLP法提出的作业单元相互关系的密集表示法,形成了一种以大量图表分析为手段,以物流费用最小为目标,物流关系分析与非物流关系分析相结合,求得合理的布置方案。
2.3 改进的SLP方法
尽管SLP方法开创性的解决了物流中心的布置问题,可是它仍然存在着一些问题。传统的SLP方法在对功能区进行相互关系分析时,受主观因素影响的因素比较大,容易忽略或掩盖一些非物流关系对功能区布局的影响,是功能区布局出现偏差,导致布局方案不够完美。而且,传统的SLP方法对物流中心内外的交通因素考虑的较少,这给后期物流中心运营时交通组织方面留下了很大的隐患。本文是从传统SLP方法的不足入手,对其进行数学方面的改进。在建立功能区相互关系表时,考虑交通因素的影响,得到较为合理的功能区相互关系表,采用数学的方法,建立最大综合相互关系和成本最优两个目标的模型,制定约束条件,利用遗传算法求解最优的布局方案。
2.4 数学模型
2.4.1 模型假设
由于物流中心的布局问题是NP难题,对一些数据进行理想化处理。假设该铁路物流中心的功能局均是建立在同一个平面上的。物流中心的规划区域及各功能区的形状均为规则的矩形,建立坐标系,使得物流中心及其内部功能区的边分别与X轴和Y轴平行。考虑到既有条件的限制,铁路装卸线的位置是固定不变的。
2.4.2 定义参数
定义的参数有:n为物流中心功能区数量;(xi,yi)为功能区i的中心点坐标;(xj,yj)为功能区j的中心点坐标;H为物流中心规划区域的长;V为物流中心规划区域的宽;hi为功能区i的长;vi为功能区i的宽;hj为功能区j的长;vj为功能区j的宽;pij为功能区边界之间的最小距离;Tij为功能区i与j之间的综合相互关系值,由分析物流关系与非物流关系后确定;dij为功能区i与j之间的曼哈顿距离,dij=|xi-xj|+|yi-yj|;bij为功能区i与j之间的邻接度,由dij转化得到;qij为功能区i到j的日均物流量;fi为货物在功能区i所产生的固定费用,包括加工、存储、包装等费用;c为功能区之间货物单位距离的平均搬运成本,在本文的实例中c=0.05。
2.4.3 目标函数及约束条件
建立以物流中心内部功能区之间总的综合相互关系(Z1)最大和物流中心总成本(Z2)最优为目标的模型
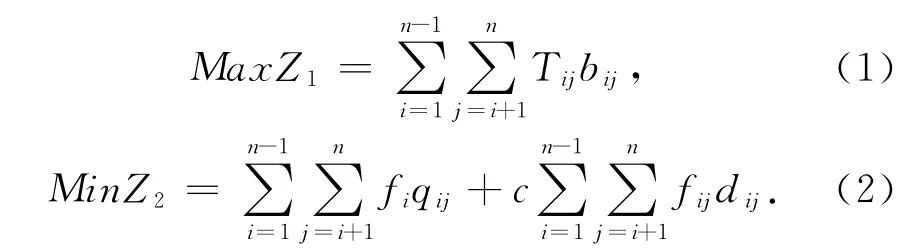
将(1)(2)式转化为单目标函数,引入权值w1和w2,由此可得到单目标函数
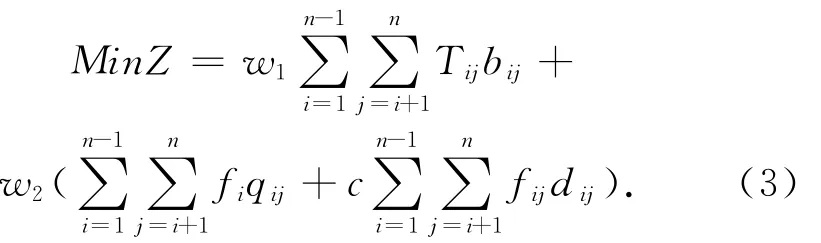
其中,w1为综合相关度的权值,w2为物流中心总成本的权值,两者均通过专家打分获得,且w1+w2=1。
目标函数需满足如下约束条件:
1)两个相邻的功能区不重叠约束

2)各功能区的边界不能超出物流中心规划区域的约束
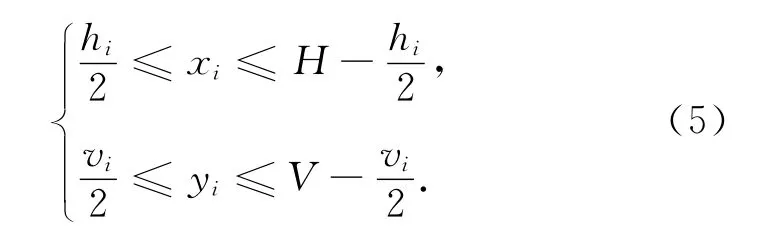
3)铁路装卸线位置的约束,即在铁路装卸线这个功能区内不能布置其他的功能区

4)物流中心出入口约束,物流中心出入口只能设置在物流中心规划区域边界上,因此,出入口中心点的坐标只能为xk=[0,H],yk=0;或者xk=0,yk=[0,V];或者xk=[0,H],yk=V;或者xk=H,yk=[0,V]。此外,如果铁路线设置在物流中心的某条边界上时,则不能在此边界上设置物流中心的出入口。
2.5 遗传算法求解
鉴于遗传算法在解决组合优化问题上的优势,本文决定利用遗传算法来求解铁路物流中心内各功能区布局的问题。
针对于治疗效果主要分为三个等级,当治疗后48h后大便性状正常,次数明显减少,其临床症状明显消失为显效;而治疗后48~72h内大便采恢复正常,临床症状消失则为显效;如果患儿治疗时间超过72h,临床症状以及大便均无明显变化则为无效[2]。
2.5.1 设计染色体
根据功能区布局优化设计的要求,设计染色体基因的形式为(xi,yi),染色体由基因串所组成。
2.5.2 初始化
初始种群采用随机方式产生,并且每组初始解必须满足边界不重叠约束和功能区边界不能超出物流中心规划区域边界的约束。
2.5.3 选择算子
本文采用最优保存策略和轮盘赌相结合的方法进行选择。使当前群体中性能最优的个体以更高的生存概率保存下来,用它来替换本代群体中经过交叉、变异等操作后产生的性能最低的个体。
2.5.4 交叉、变异
采用单点交叉,对个体进行两两随机配对,设置某一基因座之后的位置作为交叉点,配对的父代染色体在交叉点互换基因并进行基本位变异操作,以变异概率随机选择其中某一个或某几个基因位上的值做变异运算。
2.5.5 适应度函数
一般,适应度函数是由目标函数变换而成,本文的适应度函数为
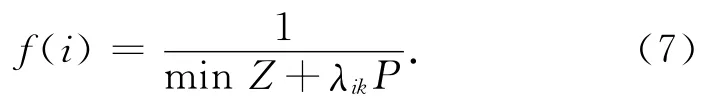
式中:λik为第i个染色体中不符合约束条件k的布局块数目,P为违反约束条件的惩罚量。
3 实例分析
3.1 算例参数
某地计划建设一个规划用地为矩形的铁路物流中心,需要铁路装卸线水平贯穿物流中心且紧靠规划用地的边界,规划用地面积为420000m2,水平边H=840m,竖直边V=500m。通过前期的查阅分析资料,得到各个功能区的需求面积,如表1所示。另外,考虑此物流中心作业量较大,因此,需分别设置两个入口和出口。
在处理综合相互关系方面,为了简化计算,本文按照物流关系与非物流关系同等重要考虑。也就是说,对于每个功能区之间的物流关系和非物流关系密切程度相同。对密切程度量化取值:最密切为4;非常密切为3;密切为2;比较密切为1;不太密切为0;不密切为-1。这样,就可以得到综合相互关系Tij,如表2所示。各功能区之间的邻接度bij由dij来确定,将数值区间[0,dmax]划分为6个子区间(其中,dmax为物流中心规划区域长边与宽边的长度之和),dij所处子区间的对应邻接度量化如表3所示。

表1 需求面积指标
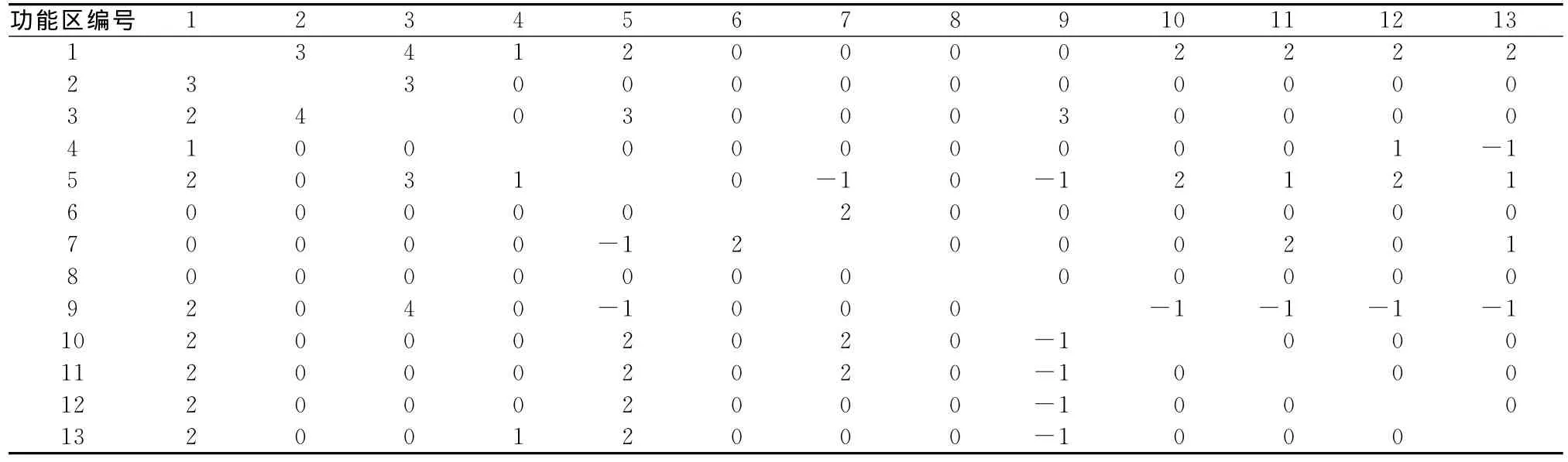
表2 功能区综合相互关系表

表3 邻接度量化表
根据分析初始数据和查阅相关资料,整理得出各功能区边界之间的最小距离pij的矩阵P,货物在各功能区所产生的固定费用fi的单行矩阵F,以及各功能区之间的日均物流量qij的矩阵Q,分别如式(1),式(2),式(3)所示。


此外,已知铁路装卸线是作为物流中心的固有设备并且贯穿整个物流中心,假设其中心点的坐标为(420,20),所以,铁路装卸线功能区范围可表示为D9=(0≤x≤840,10≤y≤30)。
3.2 遗传算法求解
根据查阅的文献资料及大量的实验结果,假设的遗传算法环境参数如表4所示。

表4 遗传算法参数表
采用Maltlab编程对算例进行求解,得到最优的染色体为{(135.1,92.2),(141,6,220.3),(433.5,202.6),(132.5,379.8),(356.4,430.8),(444.5,400.9),(541.7,462.8),(680.7,433.8),(465,10),(0,314.7),(0,232.2),(514.8,500),(820,346.6)},产生的代数为422,效果如图1所示。
4 结束语
铁路物流中心的布局问题已经成为物流系统建设的一个重要的问题,其布局的合理性直接影响到铁路物流中心乃至整个区域物流的经营效率。本文仔细分析了铁路物流中心的运作模式,对物流中心进行了详细的功能划分,用数学的方法对SLP方法进行改进,从而更完善的解决物流中心的布局问题。在整个布局的过程中,按照传统的SLP方法对物流中心各功能区之间的综合相互关系进行量化,构建综合相互关系最大的目标函数;同时,再构建物流中心总成本最优的目标函数;然后经过归一化处理,得到功能区布局方案最优的单目标函数;最后,通过遗传算法对目标函数进行求解,得到最优的功能区布局方案。通过算例的验证,本文的方法在功能区布局问题上较为合理,具有一定的指导意义。
[1] GEORGE 1.An Integrated Model and a Decomposition-Based.Approach for Concurrent Layout and Material Handling System Design[J].Computer and Industrial Engineering,2007,52(1):459-485.
[2] 唐秋华,肖飞,王雪兰.基于SLP和Flexsim的车间重构研究[J].武汉理工大学学报,2008,32(5):896-899.
[3] 李波,王俊.汽车总装线建模与仿真研究[J].电子科技大学学报,2008,37(5):789-792.
[4] 林立千.设施规划与物流中心设计[M].北京:清华大学出版社,2003:103-117.
[5] 苏超.物流中心功能区布局规划[D].成都:西南交通大学,2010:26-30.
[6] 王英林,吴慧中.空间布局的约束图方法[J].软件学报,1998,9(3):98-105.
[7] 金哲,宋执环,杨江新.可重构制造系统工艺路线与系统布局设计研究[J].计算机集成制造系统,2007,13(1):7-12.
[8] 曾议,竺长安,沈连婠,等.基于群智能算法的设备布局离散优化研究[J].计算机集成制造系统,2007,13(3):541-552.
[9] 陈希,王宁生.基于遗传算法的车间设备虚拟布局优化技术研究[J].东南大学学报,2004,34(5):627-631.
[10] 朱德辉,何世伟.铁路罐式集装箱空箱调配优化模型及遗传模拟退火算法[J].中国铁道科学,2008,29(6):104-110.
[11] 马成林,毛海军,李旭宏.物流园区内部功能区布局方法[J].交通运输工程学报,2008,8(6):116-121.
[12] 冯芬玲,景莉,杨柳文.基于改进SLP的铁路物流中心功能区布局方法[J].中国铁道科学,2012,33(2):121-128.
[13] 袁凯瞳,吕高腾,李大为,等.现代物流中心选址分析[J].交通科技与经济,2012,14(6):35-38.

