基于有限元分析的客车振动试验研究

王 涛，李宏玲

（1.安徽江淮汽车股份有限公司，合肥 230601；2.合肥工业大学机械与汽车工程学院，合肥 230002）

本文主要采用模态分析和谐响应分析来找出客车振动的原因。通过模态振型和频率的初步分析得知，怠速工况下的整车振动可能是由发动机的二阶激励引起的；通过整车的谐响应分析验证了模态分析的正确性，证明了发动机二阶激励是造成怠速时客车共振的激励源。在此基础上，通过对发动机激振频率和客车固有频率的优化来避开共振。

1 有限元建模及验证

1.1 客车车身模型简化

客车有限元模型的建立首先是对车身骨架结构的离散化。离散化的原则是模型要既能反映工程结构的主要力学特性，又要控制解题规模。客车车身是一个极为复杂的空间结构，因此，在建模时，应采取以下措施[1]。

1）略去非承载构件。如风窗玻璃的鼻梁、前保险杠和装饰件等，这些构件的变形和内力分布影响很小。

2）对构件的截面形状作适当简化。如乘客门的立柱要考虑乘客门的安装等。

3）对于空间叠交的两焊接梁，若中心线之间的距离a较大，平移其中一梁中心线将引起不可忽略的误差，则可在模型中加一根长度为a的连接梁。

4）对于两同向焊接梁，因其焊接强度近似于材料内部强度，故可将其简化为一根梁。

5）将整车约束和载荷作用点作为梁单元节点。

6）简化曲梁为直梁，如顶盖横梁、前后围处的梁。

7）主从节点原则[2]：对结构模型可能产生的病态问题，位置较近的构件结合点采用适当合并，考虑主从节点原则处理，来避免实际计算中可能导致的病态方程。

8）未考虑蒙皮的影响，骨架更趋于安全合理。

1.2 异型梁的应用

在ANSYS中，梁的截面属性生成有两种方法[3]：一种是规则的、常见的横截面，如矩形面、环形面、工字形等，只需要指定相关几何参数，软件便可自动生成；另一种是不规则截面，可通过建立相应的截面几何和有限元网格后，生成特殊的ASCII文件。在进行网格划分时，读取相关信息，生成特定的截面。图1为有限元模型中采用的部分不规则的梁截面。采用异型梁建模有如下优点：在满足强度要求的同时，实现等强度设计；有利于减轻车身骨架的质量。

1.3 载荷及约束的处理

1）集中载荷。发动机、油箱、转向系统、轮胎等的重量都是以集中载荷的形式施加在节点的。

2）结构的自重、惯性力等都作为分布载荷施加。

3）约束条件的处理。根据不同工况，对客车骨架的悬架安装点进行约束；要约束足够的自由度，消除结构的刚体运动，获得确定的位移。

1.4 整车骨架模型的建立

客车车身骨架主要采用16Mn材料，其屈服强度为280～350 MPa[4]。车身骨架采用空间梁单元BEAM188；车架结构采用板单元SHELL63，从而形成板梁结合的模型，如图2所示。模型的总节点约59 678个，总单元约58 083个（Beam188单元约28 208个，Shell单元29 327个）。

1.5 电测验证

表1是部分关键部位的静态电测和计算结果的比较。由于模型简化，试验和计算结果有偏差，但两者在总体趋势上是一致的，从而证明所建有限元模型是正确的，为后续的车身骨架结构分析提供了可靠的保障[5]。

表1 部分关键部位的计算结果和试验结果 MPa

2 整车模态分析

在ANSYS中对客车有限元模型进行模态解析计算。计算时，解除静态整车载荷及约束，使整车模型处于自由状态。本文取整车结构的保留模态数为14，整车固有频率及部分固有振型见表2、图3和图4[6]。

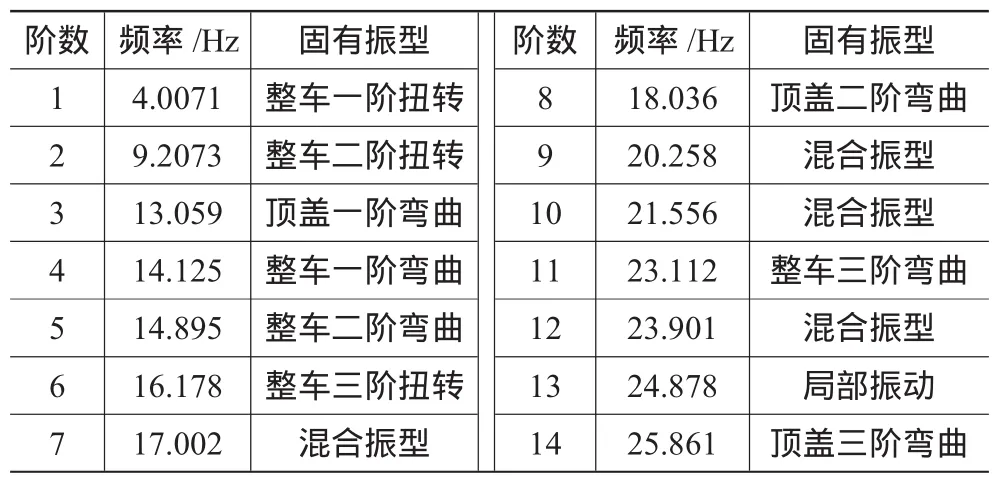
表2 前16阶固有频率和振型特征表

在市内行驶的客车经常要遇到怠速工况，在此工况下，只有发动机是激励源。该客车采用四缸水冷发动机，根据发动机怠速频率计算公式:

式中：N为发动机怠速转速，四缸发动机为700 r/min；M为气缸数目的一半，这里M=2。因此，该四缸发动机怠速激励频率H=23.3 Hz。

整车模态分析结果表明，第11、12阶频率接近发动机怠速频率；查看这两阶模态振型，可发现第11阶整车模态振型（图3）中，后部地板出现较大变形；在第12阶整车模态振型（图4）中，中门和整车前段变形较大。因此，可初步得出结论，发动机的二阶激励可能是将第11、12阶整车模态激发出来造成怠速时整车共振的主要原因。

3 谐响应分析及振动试验

谐响应分析是用于确定线性结构在承受随时间按正弦（简谐）规律变化的载荷时稳态响应，计算结构在激励频率下的响应，并得到在激励频率作用下的响应曲线。

怠速工况下，发动机是整车唯一的激励源，所以对谐响应分析中激励的确定是通过分析曲柄连杆机构的运动学规律得出的发动机往复惯性力和惯性力矩的仿真计算公式，再将实车参数代入得出准确的惯性力和惯性力矩作为整车谐响应分析时的发动机怠速激励载荷。发动机振动作为车身振动的一个主要原因[7]。

3.1 谐响应分析边界约束条件

谐响应分析中，为消除可能的刚体运动，要对悬架进行足够的约束。同时，研究中为了更符合实际使用情况，可将悬架系统和车身组合起来进行谐响应分析。本研究中边界条件的约束处理见表3。

表3 车身悬架系统的约束

3.2 谐响应分析数学模型

结构在简谐载荷作用下受迫振动的运动方程：

式中：[C]为阻尼矩阵；{F}为简谐载荷的幅值向量；ω为激振力的频率。上式的稳态位移响应可写为下列形式：

式中：{A}为位移幅值向量，与结构固有频率ω0载荷频率ω以及阻尼[C]有关；φ为位移响应滞后激励载荷的相位角。

3.3 谐响应分析激励的处理

发动机自身的振动主要来自于发动机运转过程中产生的往复惯性力和惯性力矩。往复惯性力Fj的大小可由下式表示[8]：

式中：mi为结构中的往复运动质量；j为往复运动加速度。

3.3.1 往复运动质量

发动机的曲柄－连杆－活塞机构简化为如图5所示的三质点系统，三质点分别位于C、A、B，图5中X是活塞运动的方向。

设曲柄和曲柄销的质量为m，连杆质量m′，活塞质量m″，D为连杆的质心，曲柄的半径为r，l为连杆的长度，连杆质心于连杆大头孔中心距为b，曲柄的质心C到回转中心的半径为s。连杆质量m'分配到A、B两点为m1和m2，且连杆的质心不变，与m″合成，则得：

3.3.2 往复运动加速度

对于图5所示的曲柄连杆机构，往复运动B点的位移x可表示为

式中：λ为曲柄连杆机构的连杆比，λ=r/l 往复运动A点的速度v可表示为

由曲柄连杆机构的几何规律有：

考虑到ω=dφ/d t，则式（7）对t求导并化简可得：

将式（8）代入式（6），可得

将式（9）对t求导，可计算往复运动A点的加速度j，化简后可得：

由式（7）可知

将式（11）按牛顿二项式定理展开成如下的级数：

在实际计算中，一般只取前两项，即

当取式（12）近似时，加速度j可化简为

由式（3）和式（13）可得，发动机曲柄连杆机构的往复惯性力Fj等于质量m2与活塞加速度j的乘积，方向与加速度方向相反：

Fj1和Fj2分别称为一阶和二阶往复惯性力。因此，往复惯性力可以表示为按简谐规律随曲轴转角变化的一阶和二阶惯性力之和[9]。

活塞在运动过程中还会有惯性力矩产生，而连杆、曲柄在运动中也会产生惯性力矩。曲柄对回转中心O点的动量矩为Q1=ms2φ′

连杆对O点动量矩：Q2=[I′+m′（l-b）2]ψ′

式中：I′为连杆对其质量中心D的转动惯量。如果采用三质点模型，则可得：Q2=[I+m1l2]ψ′

I为连杆对B点的修正转动惯量，则由此可得：

m1以O点为中心角速度φ′回转运动，连杆相对与B点以角速度ψ′回转，因此，Q2还可以表示为

Q1与Q2相加即可得机构的总动量矩。根据动量矩定理，可知惯性力矩M0可表示为

3.4 谐响应计算分析

发动机的怠速转速n取700 r/min，转化为角速度是ω=2πn=1 400 π rad/min，往复运动质量 m2=4.95 kg，曲轴半径r=0.08 m，曲柄连杆机构连杆比λ=r/l=0.256，杆转动惯量 I′=366.9 kg·mm2，将这些数值代入式（14）和式（15），将得出的Fj、M0的幅值加载发动机悬置连接处节点。查钢材料资料，将阻尼比设置为0.035。

在ANSYS中进行整车在发动机激励下的谐响应分析[10]。选取中门立柱、前中后地板、四个悬置点的位移量随频率变化的曲线，来评价整车的响应情况。该客车发动机的额定转速为3 000 r/min，对应发动机激励H=（3 000/60）×2=100 Hz，因此，取 0～100 Hz频率范围作为发动机的激励范围，并在此频率范围内对整车模型进行谐响应计算，频率间隔为5 Hz。

图6是中门立柱XYZ方向位移量随频率的变化关系。由图可知X方向（客车前进方向）的位移量大于另两个方向，在24 Hz和50 Hz处出现峰值。图7是地板上的前中后三个位置的垂向位移随着频率的变化关系，中、后部位分别在24 Hz处出现了峰值，前部由于离发动机较远，在44 Hz处出现了峰值，但是其数值相对中后部地板偏小。图8是四个悬置点的垂向位移量随频率的变化关系。可以看出，后悬置点的竖直向位移量比前悬置点大，说明后悬置点垂向受发动机影响明显，后悬置点处的阻尼选取要比前悬置点处的大，才可以满足减振要求。

客车发动机怠速转速为700 r/min，由此换算得发动机怠速激振频率为23.3 Hz。综合分析可知，测点位移量在24 Hz达到最大值可能是由发动机二阶共振频率引起。若考虑到实际中发动机的激励相互叠加，对比前面的整车模态分析结果和局部振型图9和图10，可知是发动机二阶振动频率23.3 Hz（怠速频率）激起了整车振动，验证了模态分析的正确性。

3.5 整车行驶振动试验

本文通过客车行驶振动试验，在车架和车身部分位置布置加速度传感器，采集振动数据。

通过对客车中门立柱自谱的分析，振动主要出现在15～30 Hz频段内，由图11和表4可以看出，在25 Hz左右出现峰值，十分接近发动机怠速激励频率23.3 Hz。所以怠速时中门的振动是由发动机二阶激励与整车发生共振引起的，也验证了模态分析和谐响应分析的结果。

表4 10号测点（中门立柱）数据表

4 结论

本文在分析怠速工况下发动机引起的车身振动时，先对客车结构进行模态分析，再通过对发动机怠速激励的理论仿真进行客车的谐响应分析并进行实车的行驶振动试验验证，得出了发动机的二阶激励是引起车身共振的原因。

[1]石琴.基于现代设计理论的车身结构设计方法研究[D].合肥：合肥工业大学，2006.1.

[2]王涛，王海朔，朱清君.客车车身静态与模态分析研究[J].安徽化工，2010，36（2）:19-22.

[3]石琴，张代胜，谷叶水，等.大客车车身骨架结构强度分析及其改进设计[J].汽车工程，2007，29（1）:87-92.

[4]王海霞，汤文成，钟秉林，等.CJ6121GCHK型客车车身骨架有限元建模及结果分析方法研究[J].汽车工程，2001，（1）

[5]朱茂桃，刘星荣，韩松涛.轻型客车车身有限元分析与试验研究[J].东南大学学报，1999，（11）

[6]高玉华，李华香，张代胜.半承载式车身骨架有限元建模和分析[J].合肥工业大学学报，2007，30（4）

[7]庞剑，谌刚，何华.汽车噪声与振动-理论与应用[M].北京：北京理工大学出版社，2006:215-242.

[8]杨仕.摩托车动态设计及其性能评价方法研究[D].重庆：重庆大学，2009.5.

[9]阮杰.摩托车车架结构分析及发动机振动的影响研究[D].武汉：武汉理工大学，2007.5.

[10]尚晓江，邱峰，赵海峰，等.ANSYS结构有限元高级分析方法与范例应用[M].北京:中国水利水电出版社，2008：87-108.