风帆助航船舶帆角控制系统分析与设计*
李向舜 杨 幸 严新平 徐 立
(1.武汉理工大学自动化学院 武汉430070;2.武汉理工大学能动学院 武汉430063)
0 引 言
风能是自然界取之不尽、用之不竭的巨大能源。据估计,全球每年可以利用的风力总能量为2×107MW,为地球上可资源化利用的水能总量的10倍[1]。合理开发和利用风能可有效的节约石化能源,并降低碳排放。此外,世界上90%以上的国际贸易是通过船舶来实现的[2],对航线上的风能进行开发利用,可以有效降低船舶的运营成本,减少能耗,降低碳排放[3]。对于船舶运输业来说,风力助航作为一种节能方式存在很大的发展潜力,同时风力助航也符合绿色船舶的发展理念。
风帆辅助推进混合动力船舶越来越受到人们的关注[4-7]。国外在风帆-柴油机混合动力技术上起步较早[8]。国内学者在近几年也对风帆辅助混合动力船舶做了一些有意义的工作。文献[3]对船舶安装风帆的节能效果进行了研究,结果表明大部分船舶安装风帆的节能效果可达4%~10%。另外,文献[9]也对风帆辅助船推进性能进行了分析和计算,讨论了节能效果与帆船选择、帆机浆船的工况匹配等问题,同时也对节能效果进行了估计。还有一些学者从空气动力学的角度,对帆船的选择、风帆的形状、风向大小等问题上进行了计算[10-11]。目前,关于船舶航向控制方面的成果已经比较丰富。然而,关于风帆助航船舶的航向控制方面的成果却不多见,一些学者仅是把风当做干扰项,并未对风作用于风帆产生的力进行定量分析,关于风帆的控制更是少见。
运输船舶加装风帆辅助推进装置后可节省燃油消耗并可以有效降低碳排放量,但是加装风帆势必也会对船舶推进系统产生影响,并可能使船舶产生一定的偏航,严重时甚至会发生事故。因此,对船舶的帆角控制是十分必要的。
从已有的文献来看,对于风帆助航船舶的研究主要集中在帆的类型与结构及其动力性的研究。文献[3]主要针对风帆节能效果进行了分析,而文献[9]主要针对船舶加装风帆后的机、桨匹配问题进行了探讨。文献[10]主要针对帆的结构,从空气动力学的角度给出了安全性计算,并对风帆辅助推进装置的结构组成进行了设计,对其建立了数学模型。本文对风帆助航船舶装置的控制系统进行了设计,主要针对系统稳定性和控制器参数选取方法进行了分析与设计。
1 问题描述
风帆辅助推进装置系统原理框图见图1[13],该系统为串级控制系统,其包括主回路和副回路。副回路为变量泵排量控制系统,主回路为帆角控制系统。主回路指令信号一般由风向决定,它与帆角传感器反馈信号比较后经过主帆角控制器送至副回路控制系统中。副回路给定值为帆角控制器的输出,反馈值为位移变送器输出的位移量,其输出还作为变量泵排量的指令信号,控制变量泵变量机构的摆角,从而控制变量泵的排量,进而控制液压马达的转角,最终控制了帆翼的转角。
控制系统等效结构图见图2。

图1 风帆辅助推进装置系统Fig.1 Sail assisted ship system

图2 风帆辅助推进装置系统等效结构图Fig.2 The equivalent diagram of sail assisted ship system
副对象的传递函数[10]为
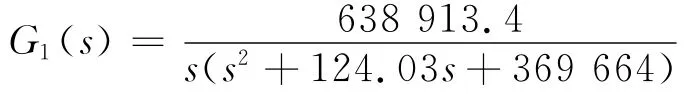
主对象的传递函数[10]为
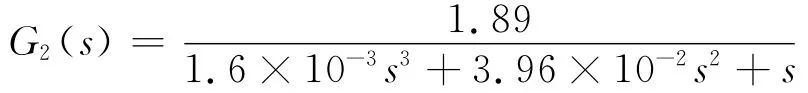
位移传感器的反馈系数为50,角度传感器为单位反馈,即为1。其中主副控制器即为所需整定的参数。
在串级控制系统中主控制器起定值控制作用,副控制器起随动控制作用。副控制器一般选用P调节。主参数是生产工艺的主要控制目标,一般不允许有残差。所以,主控制器一般选用PI调节。而由主对象的传递函数可以看出已经包含了积分环节,所以主控制器选用P即可。
2 主要结果
2.1 稳定性分析
包括主回路和副回路稳定性分析,主要通过Routh稳定判据确定主副控制器参数选取范围。
针对副回路,设副控制器的控制规律为

副回路的开环传递函数为
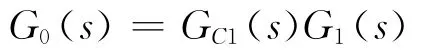
副回路的闭环传递函数为
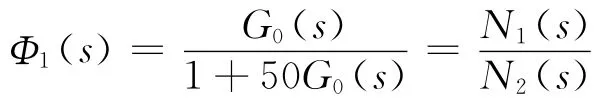
式中:N1(s)=638 913.4K1;

副回路闭环传递函数的特征方程为

要使系统稳定,利用劳斯稳态判据,见表1。

表1 副回路劳斯稳态判据表Tab.1 The Routh stability of vice-loop
要使该系统稳定,则劳斯表中第一列数需大于0,则0<K1<1.44。
这里,可取K1=1.2。
针对主回路,设主控制器的控制规律为

主回路的开环传递函数为

式中:N3(s)=1.449 1×106K2;N4(s)=1.6×10-3s6+0.238s5+597.374s4+76 098s3+1.887 7×106s2+3.833 5×107s。
主回路的闭环传递函数为
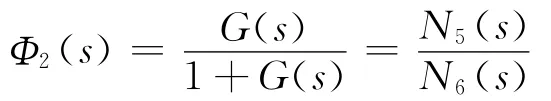
式中:N5(s)=1.449 1×106K2;N6(s)=1.6×10-3s6+0.238s5+597.374s4+76 098s3+1.887 7×106s2+3.833 5×107s+1.449 1×106K2。
主回路闭环传递函数的特征方程为

要使系统稳定,同理利用劳斯稳态判据可得

这里,可取K2=188。
2.2 模糊P控制
主控制器采用的是模糊P参数自整定的方法。总体思路是先由采样时刻所获得的误差及误差变化信号,再把它们量化到论域上的值模糊化,经过模糊推理和解模糊得到控制量即P的变化量,从而改变P的大小,使模糊控制器具有自适应能力。这种形式的模糊控制器具有结构简单,参数可调的特点。
模糊控制步骤包括模糊化、模糊推理和解模糊。模糊控制器的结构框图见图3。

图3 模糊控制器结构Fig.3 Fuzzy control diagram
1)模糊化。如图3设计中采用二维模糊控制器,输入变量选为给定值与输出反馈值的偏差以及偏差的变化率。首先将输入量进行论域变换,把偏差变换为[0,6]之间的数值,偏差变化率变换为[-3,3]之间的数值。然后把得到的数值通过单值模糊器模糊化,得到一个关于该数的隶属度模糊矢量。在设计中,先用经典PID控制算法选取主调节器的一个Kp值,得到偏差及偏差变化率的变化范围,然后将实际范围乘上量化因子,将其转化到[0,6]中。在设计中选取Kp的值为298,得到偏差范围为[-0.27,1],偏差变化率范围为[-4.33,10.48]。
2)模糊推理。定义了论域以后就要确定模糊集合,文中选择NB、NM、NS、NO、PO、PS、PM、PB7个模糊集合,分别代表负大、负中、负小、零、正大、正中、正小,每个集合都有一定的范围,这样能够精确地将输入量变换到模糊集合当中。模糊语言值实际上是一个模糊子集,而语言值最终是通过隶属函数来描述的,确定隶属函数首先要选择隶属函数的形,在设计中,输入采用高斯隶属函数,输出采用三角隶属函数。模糊集隶属度函数的形状,对控制器的特性影响不大。模糊规则是根据以往经验,通过不断调整推导出输入输出的模糊关系。模糊规则见表2。然后再确定模糊推理机的类型,文中采用的推理方法是Mamdani,与运算方法是min,或运算方法是max,模糊蕴含方法是min,模糊聚集方法是max。matlab中所使用的推理方法均为独立推理,具体的步骤是:

表2 模糊规则表Tab.2 Fuzzy rule
输入输出隶属函数见图4。

图4 输入输出隶属函数图Fig.4 Membership function
输出的模糊控制器见图5。
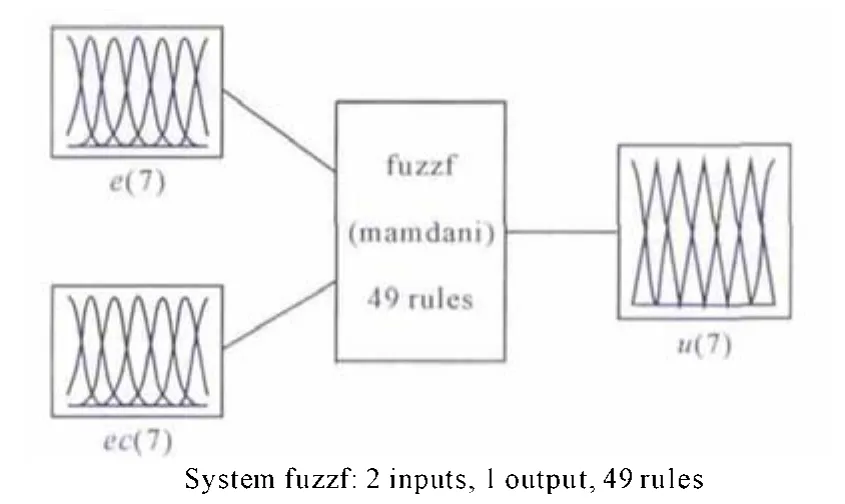
图5 模糊控制器Fig.5 Fuzzy controller
3)解模糊。本设计运用的解模糊方法为最大隶属度平均法,即在推理结论的模糊集合中取隶属度最大的那个元素作为输出,当有几个元素的隶属度同时最大时,则取这几个元素的平均值作为输出。然后将模糊控制器的输出进行论域反变换。在设计时首先让KP为298,在此基础上加上模糊器输出的值乘上比例因子,即得在此时输入偏差以及偏差变化率的数值下控制器的参数值。
需要说明的是,其中量化因子和比例因子的选择是至关重要的,它们的选择都需要在实验中不断地调整,量化因子并不是完全根据计算得到,需要根据控制效果作适当改进。
3 Matlab仿真与分析
3.1 Matlab仿真
当输入为阶跃信号时,主控制器在经典P控制器下输出仿真图见图6,模糊控制P下主回路的仿真图见图7。
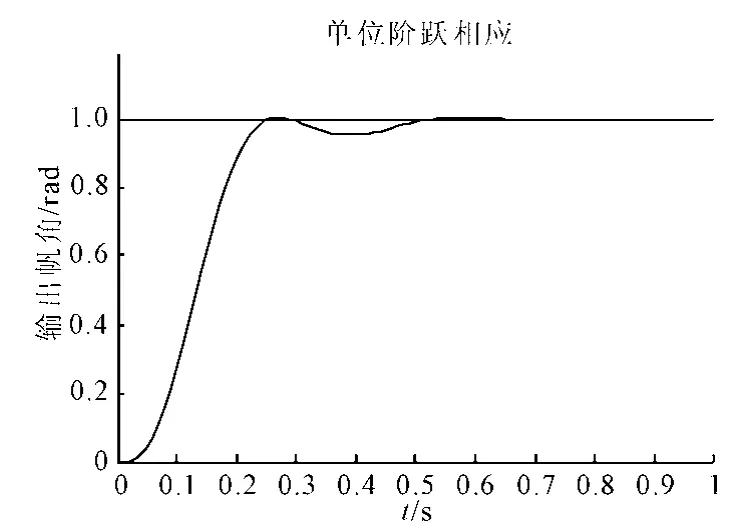
图6 经典P控制输出波形图Fig.6 Output simulation waveform diagram by classical P
3.2 仿真结果分析
由图6与图7对比可以清楚的看出,运用模糊控制器得到的仿真波形没有出现超调,在阶跃输入作用于系统0.4 s以后输出就能很好的跟踪输入。而经典P控制器的输出则有波动,在跟踪一段时间后又出现偏差,这在工程上是不允许的。因此,选用模糊控制器能达到很好的控制效果。

图7 模糊P控制输出波形图Fig.7 Output simulation waveform diagram by fuzzy P
4 结束语
通过仿真对比可以看出,经典的P控制达不到模糊控制的效果,模糊控制可以达到快速稳定跟踪的要求。设计的模糊控制器只含有比例环节,相对较容易改变参数。模糊控制器是在Matlab中编程实现的,通过模糊化、模糊推理以及解模糊,得到模糊控制器,最后调用模糊控制器,求得动态的主控制器。
[1] 李全林.新能源与可再生能源[M].南京:东南大学出版社,2008.
[2] Fujiwara T,Hearn G E,Kitamura F,et al.Steady sailing performance of a hybrid-sail assisted bulk carrier[J].Journal of Marine Science and Technology,2005,10(6):131-146.
[3] 孟维明,赵俊豪,黄连忠.风帆助航节能船的应用前景[J].船舶,2009,20(4):1-3.
[4] 任洪莹,黄连忠,孙培廷,等.大型风帆助航船舶综合节能减排潜力分析[J].大连海事大学学报,2010,36(1):27-30.
[5] 严新平.新能源在船舶上的应用进展及展望[J].船海工程,2010,39(6):111-115.
[6] 郭 浩,张 晰,安居白,等.基于船舶AIS信息的可疑船只监测研究[J].交通信息与安全,2013,31(4):67-72.
[7] 黄朝明.船舶风帆助航的实验研究[D].大连:大连海事大学,2008.
[8] 胡以怀,王友聪.日本风帆助航船舶的研究进展[J].绿色大世界:绿色科技,2009(7):103-106.
[9] 于小虎,刘寅东,张英俊,等.船舶混合动力系统的研究[J].大连海事大学学报,2011,37(4):35-38.
[10] 王立明.风帆辅助推进装置及控制系统的建模与仿真研究[D].武汉:武汉理工大学,2010.
[11] Ueno M,Tsujimoto M,Takekawa M,et al.Fundamental research for development of an advanced sail-assisted ship[J].IEEE Techno-ocean.2004(4):1102-1109.

