基于模糊逻辑的单交叉口交通信号控制方法设计及实现*
赵建玉 郭仲林 郑显臣
(济南大学自动化与电气工程学院 济南250022)
0 引 言
现有的交叉路口的信号灯控制方法有固定配时控制、感应式控制和自适应控制。由于在城市交通系统中,到达交叉路口的车辆具有随机性、复杂性的特点,想要建立准确的数学模型来描述它很困难。在实际应用中固定配时控制与感应式控制的效果不能完全令人满意。以SCOOT为代表的自适应控制系统能够根据实时交通状况自适应的调整信号配时,控制效果较好,但其控制精度受下游停车线断面流量图式的预测精度的影响,对我国复杂的交通形式没有起到很好的效果[1]。
模糊数学针对的研究对象通常是那些包含非定量信息的不确定性系统,它能利用模糊集的概念将不确定信息定量的表示,并以接近人的形象思维方式进行定性分析和推理[2]。因此模糊数学在解决交通系统问题上有很好的效果。
1 排队车辆检测及相位确定
图1为道路交叉口示意图。因为右转的车辆可随时通过,不会对交通灯的控制产生影响,所以右转的车流在控制中就可以不考虑。规定以下相位:
第1相位。南北左行。
第2相位。南北直行。
第3相位。东西左行。
第4相位。东西直行。
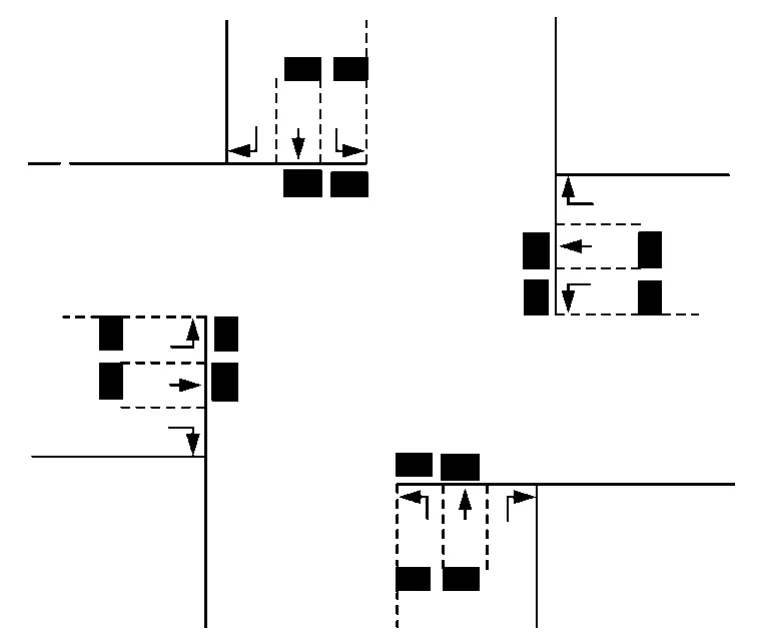
图1 道路交叉口示意图Fig.1 Schematic road intersection
在公路的左转相位和直行相位对应的道路上安装1.8 m×1.8 m的单回路检测器,放置在路口近端及距离路口近端100 m处,用以检测每个相位的排队车辆数[3]。每当路口近端的检测器检测到有车经过时,表示该相位离去1辆车;每当距路口近端100 m处的检测器检测到有车经过时,表示该相位到来1辆车。则
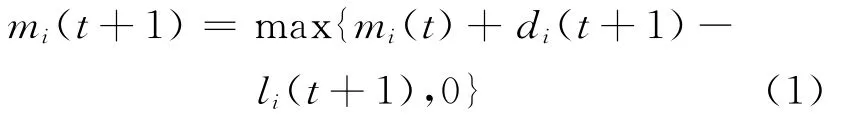
式中:mi(t+1)、di(t+1)和li(t+1)分别为t+1 s内第i相位的排队车辆数、到达的车辆数和离去的车辆数。
由于南—北、北—南以及东—西、西—东方向的左转、直行交通灯的控制是一致的,所以对于同一相位,如南—北直行和北—南直行,我们取排队车辆数较多的那一个相位的排队车辆数作为该相位的排队车辆数。
2 相位选择控制器与绿灯延时模糊控制器设计
2.1 相位选择控制器设计
2.1.1 相位选择控制器的输入、输出
设当前第i红灯相位的排队车辆数为ai(i=1,2,3或1,2,4或1,3,4或2,3,4),持续红灯时间为bi(i=1,2,3或1,2,4或1,3,4或2,3,4)。所谓持续红灯时间表示,该红灯相位由最近一次绿灯切换为红灯的时刻一直到此刻所经过的时间。设选择出的下一绿灯相位的相位数为c。
因为当前共有3个红灯相位,要选择出一个下一绿灯相位,所以相位选择控制器有6个输入,即3个当前红灯相位的排队车辆数和持续红灯时间;有1个输出,即选择的下一绿灯的相位数。
2.1.2 相位选择控制器的相位选取规则
对于给定的输入,制定以下规则得到输出。
规则一:
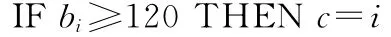
规则二:
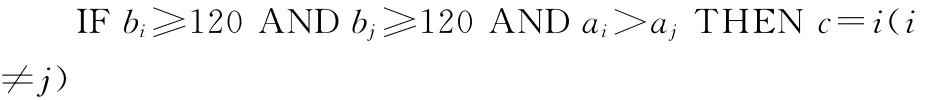
规则三:
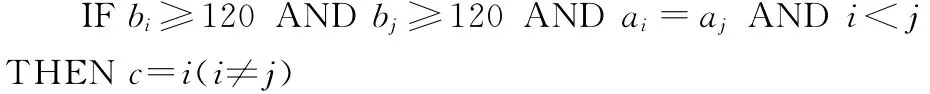
规则四:
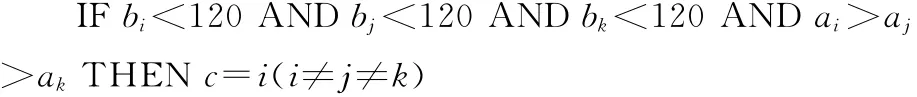
规则五:
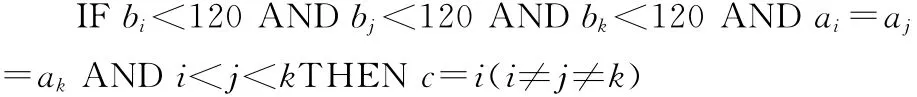
于是根据检测到的当前各红灯相位的车辆数,以及红灯相位的持续时间,确定出下一绿灯相位。
2.2 绿灯延时模糊控制器设计
2.2.1 绿灯时长及延时时间上限
设绿灯时长包括最短时间t1和绿灯延时时间t2。因为司机能够接受的红灯等待时间上限为180 s,每一相位的最大绿灯时间为60 s[4],所以根据专家经验,t1一般取20 s,t2∈[0,40]s。会出现这样的极端情况:4个相位的排队车辆都很多,但3、4相位的车辆数始终没有相位1、2的车辆数多。假设相位1、2的绿灯时间都为60 s,经过120 s后,3、4相位的司机持续等待红灯的时间为120 s,假设此时相位3、4的车辆数仍然比相位1、2的车辆数少,若相位3此时切换绿灯相位,时间为60 s,那么相位4的司机持续等待红灯的时间为180 s,达到司机持续等待红灯时间上限。所以每当切换相位前要先检测是否有红灯相位已持续等待120 s,若已等待120 s,则必须选择该相位作为下一绿灯相位[5]。
2.2.2 模糊控制器组成
模糊控制器是由以下几部分构成的,见图2。
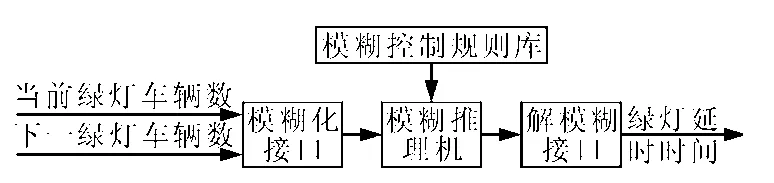
图2 模糊控制器框图Fig.2 Fuzzy controller block diagram
2.2.3 输入、输出及模糊化
模糊化接口的作用是将输入的变量转化为[0,1]上的模糊量,即要知道模糊集的论域,隶属度函数和模糊集的数量。设当前绿灯相位排队的车辆数为m1,下一绿灯相位排队的车辆数为m2。规定模糊化接口的输入变量m1和m2的取值范围为[0,40],将论域划分为11个等级,即11个模糊论域{0,1,2,3,4,5,6,7,8,9,10}。它的量化因子K1=K2=0.25,真实值m相对应的模糊论域值M=[m/4]([x]表示不大于x的最大整数)。M1、M2的模糊语言值选取{X1,X2,X3,X4,X5,X6,X7},分别代表很少、少、较少、中等、较多、多、很多。选取正态分布函数作为模糊子集的隶属函数,见图3。
设绿灯延时时间为t,规定输出变量t∈[0,40]s,将论域划分为11个模糊论域{0,1,2,3,4,5,6,7,8,9,10}。它的量化因子K=0.25。真实值t相对应的模糊论域值T=[t/4]。T的模糊语言值取值{Y1,Y2,Y3,Y4,Y5,Y6,Y7,Y8,Y9},分别代表极短、很短、短、较短、中等、较长、长、很长、极长。选取正态分布函数作为模糊子集的隶属函数,见图4。
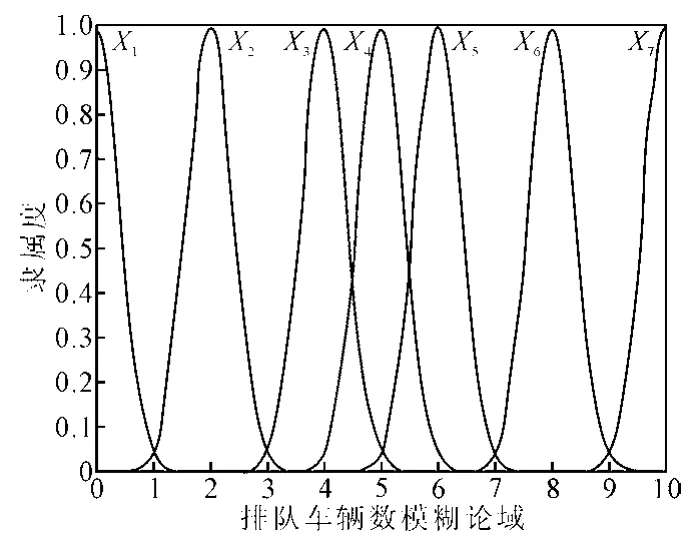
图3 排队车辆的模糊子集隶属函数Fig3 Membership function fuzzy subset of queuing vehicles
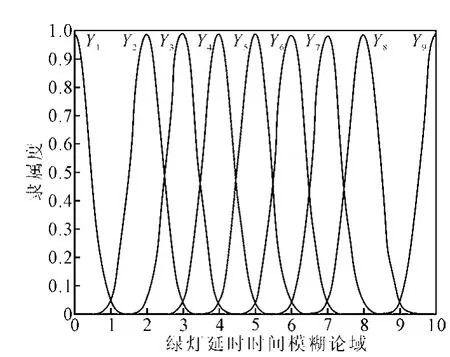
图4 绿灯延时的模糊子集隶属函数Fig.4 Membership function fuzzy subset of green light time delay
2.2.4 模糊控制的规则库
规则库是由描述模糊子集之间关系的控制规则构成,是人们对该问题的经验和知识的反映。基于路口的实际情况,控制规则有49条语句构成,分别为

把这些控制规则制作成表,见表1。
2.2.5 模糊推理与逆模糊化
模糊关系是由模糊规则表中的模糊语句决定的,因此由模糊规则表可以看出输入与输出之间的模糊关系有49个,采用 Mamdani和max-min合成推理方法计算出Ri〔i=1,2,…,49〕[6]。
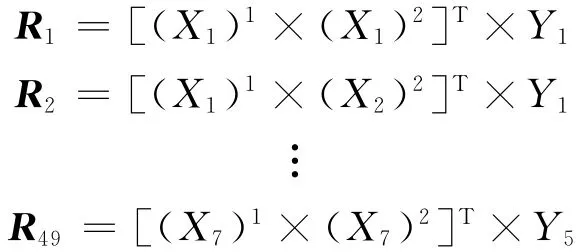
以R1的计算为例。其中:〔X1〕1为输入M1的模糊子集,〔X1〕2为输入M2的模糊子集,Y1为输出T的模糊子集。
则模糊关系矩阵为

当输入变量m1、m2分别为模糊论域M1、M2时,由模糊推理合成得到输出变量t的模糊论域:
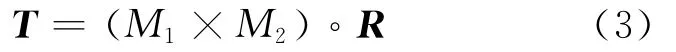
最后用最大隶属度法对模糊论域T进行逆模糊化处理,得出绿灯延时时间表,见表2。
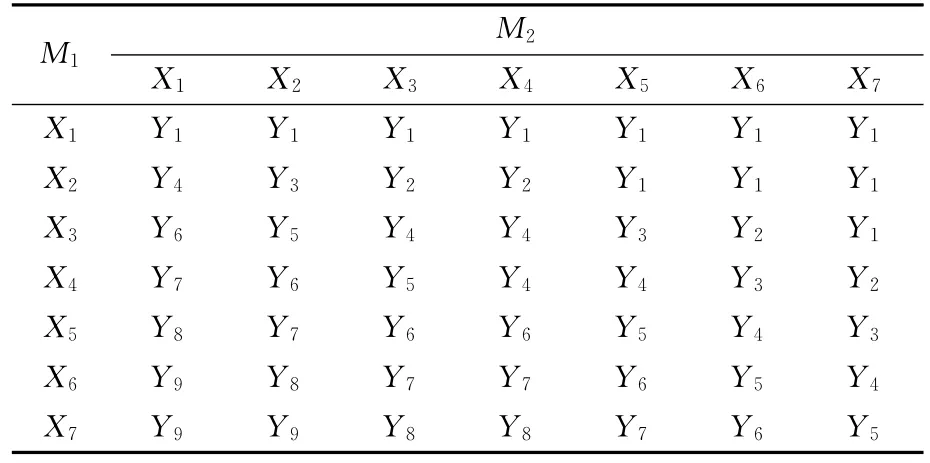
表1 交通灯模糊控制规则表Tab.1 Traffic lights fuzzy control rule table
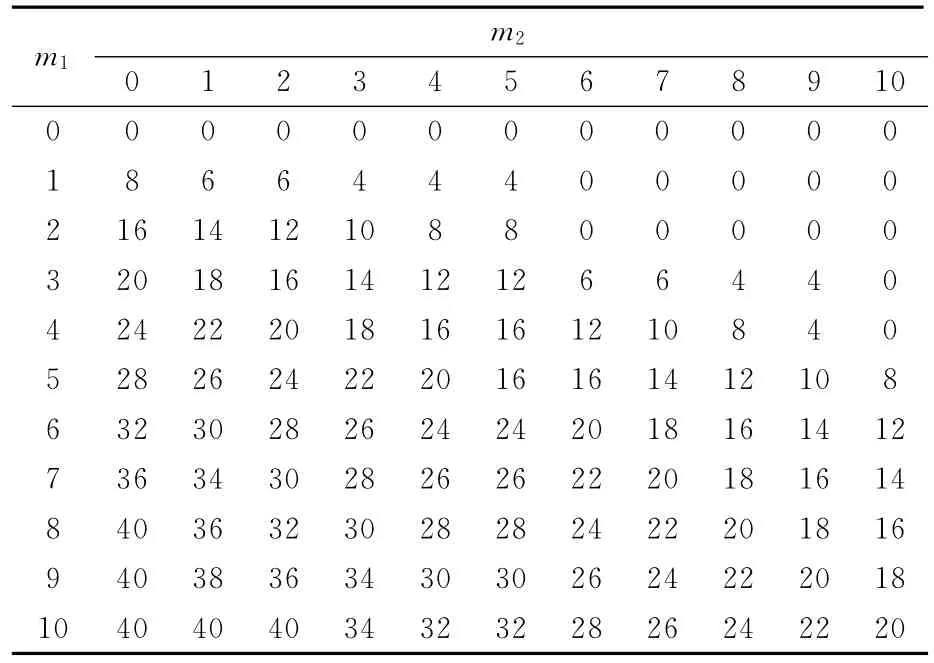
表2 绿灯延时时间表Tab.2 Green light time delay schedule s
2.3 模糊控制算法
在现行的绿灯相位绿灯时长结束前3 s,根据相位选择控制器选择下一绿灯相位,把现行绿灯相位的车辆数和下一绿灯相位的车辆数作为输入送入绿灯延时模糊控制器,若输出的延时时间为0 s,则亮黄灯3 s切换相位,进入下一绿灯相位,依次循环。若输出的延时时间大于0 s,则判断已经亮灯的绿灯时间加上延时的绿灯时间是否不小于60 s,若不小于60 s,则延时到60 s时强制切换到下一绿灯相位,在57 s时亮黄灯3 s。若已经亮灯的绿灯时间加上延时的绿灯时间小于60 s,则绿灯持续亮到延时时间结束[7]。同上在绿灯延时时间结束前3 s,根据相位选择控制器选择下一绿灯相位,把现行绿灯相位的车辆数和下一绿灯相位的车辆数作为输入送入绿灯延时模糊控制器,得出延时时间,再检测延时时间是否满足要求,依次循环。
3 排队车辆的平均延误模型
先计算红灯相位的延误时间,假设第i相位切换到红灯时,该相位在第t+1 s末的延误时间为[8]
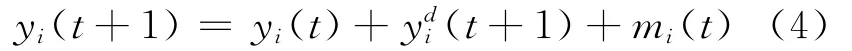
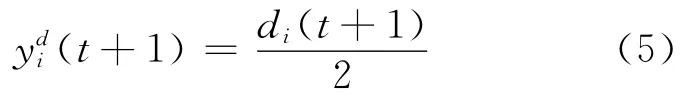
mi(t)为第i相位ts末的排队车辆数,di(t+1)为t+1 s越过距路口100 m处检测器的车辆数。
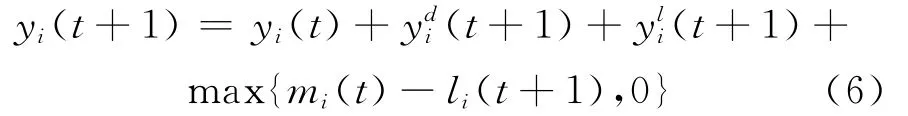
计算绿灯相位的延误时间,假设第i相位切换到绿灯时,该相位在第t+1 s末的延误时间为[8]式中:yli(t+1)为第t+1 s越过路口检测器的车辆产生的延误时间。设离去率为s,因此:
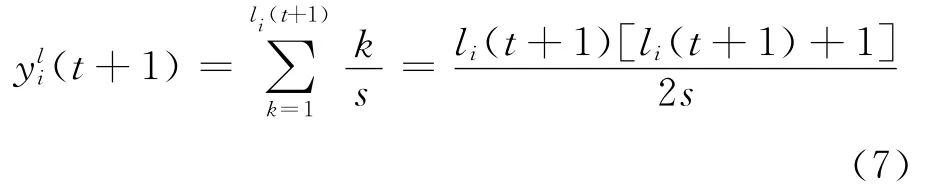
li(t+1)为t+1 s越过交通灯路口检测器的车辆数。
综上,车辆的延误时间的总和为
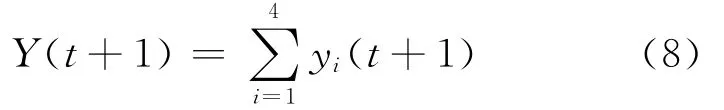
因为总的车辆数为
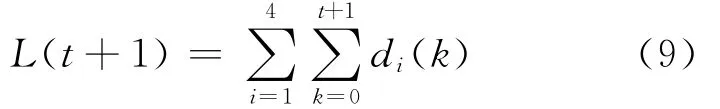
因此,路口的平均延误为
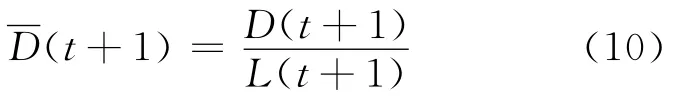
4 计算机仿真及结果分析
设计的智能交通灯模糊控制器以车辆在路口的平均延误时间为评价标准,使用Matlab进行仿真。仿真程序流程图见图5。
由于在Matlab仿真环境下无法用传感器测量到达和离开的车辆数,所以采用模拟产生车辆的方式对到达交叉路口的车辆数进行仿真:设到达交叉路口的车辆数服从参数为1的泊松分布,车辆通过绿灯的速率即离去率s=2辆/s。相位切换和绿灯延时服从已经给出的智能交通灯模糊控制器。我们假设定相位定时交通灯的相位循环切换,绿灯时间为30 s,设定仿真总时间为60 min,仿真10次,得到的数据见表3。
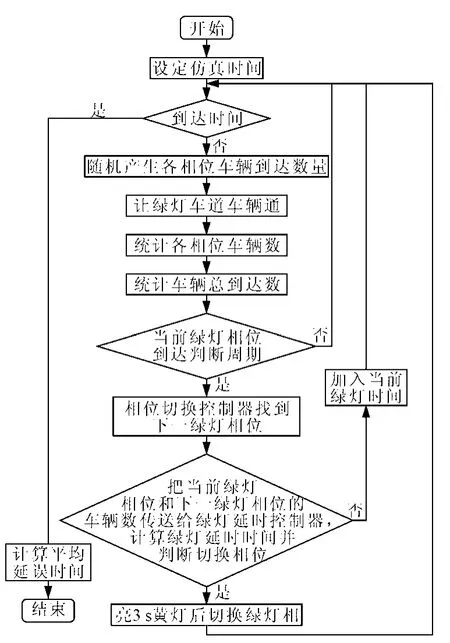
图5 仿真程序流程图Fig.5 The simulation program flow chart
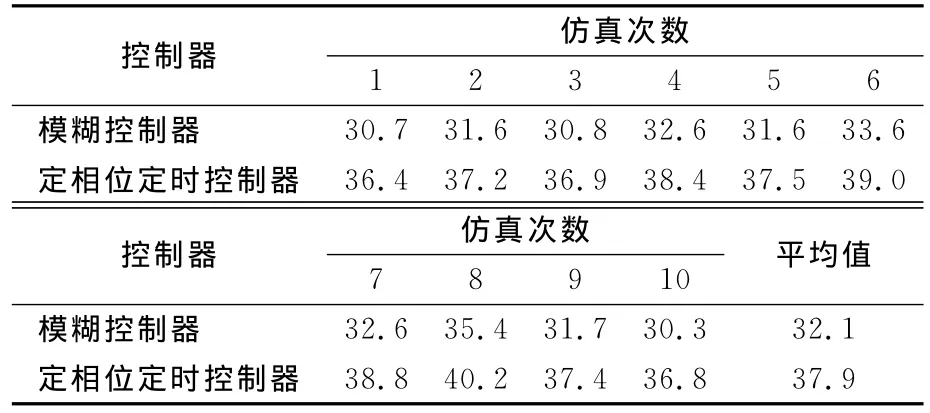
表3 车辆平均延误时间表Tab.3 Average vehicle delay schedule s
由仿真结果可以看出,采用相位选择及绿灯延时模糊控制器的智能交通灯的平均车辆延误时间为32.1 s,比定相位定时长的交通灯的延误时间37.9 s小了5.8 s,证明了基于流量控制的模糊控制器的有效性。
5 结束语
本文设计了相位选择控制器和绿灯延时模糊控制器,根据给出的车辆平均延误时间的数学模型,利用Matlab进行仿真实验,对比传统的定相位定时长控制器,证明了交通灯的模糊控制器的有效性。
[1] Xiao Jianmei,Wang Xihuai.Highway traffic flow model using FCM-RBF neural network [J].Lecture notes in computer science,2009,31(7):956-961.
[2] 谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社,2010.
[3] 臧利林,贾 磊,秦伟刚,等.基于环形线圈车辆检测系统的研究与设计[J].仪器仪表学报,2004,25(4):329-331.
[4] 邹毅峰,李夏苗.运用交通流理论确定保证交通安全的最短绿灯时间[J].长沙铁道学院学报,2006,17(2):64-67.
[5] 熊光洁,刘玉德,吴 雪,等.城市道路区域交通信号控制系统的设计与实现[J].交通信息与安全,2008,26(5):56-61.
[6] 肖业伟,黄辉先.基于蚁群算法的交叉路口多相位信号配时优化[J].计算机工程与应用,2008,44(19):241-244.
[7] 孙 超,徐建闽,丁 恒,等.基于模糊控制算法的干道信号协调控制优化[J].交通信息与安全,2008,26(4):155-157.
[8] 乔 健,宣慧玉.一种基于通行需求度的单交叉口模糊控制算法[J].系统工程,2004,22(10):59-64.

