随机区组设计的方差分析及其应用研究

张林泉

(广东女子职业技术学院,广州 511450)

1 随机区组设计的基本模式

1.1 随机区组设计的方法

先分析实验对象个体间的主要差异,以及哪些方面的差异可能会造成他们在实验中测量数据的不同,再据此选定一定的标准将实验对象划分为不同的区组,使得每个区组内被试的差异性尽可能小,区组内的被试具有同质性;最后将每个区组内的被试随机、均等地分配到各种实验处理中接受测量.

1.2 随机设计的基本模式

有b个实验处理、实验对象被划分为a个区组,每个水平组合有n次重复,其中每个区组内的实验对象是实验处理的整数倍(至少为1倍,保证一个区组能向每一实验对象处理分配一个实验对象),以便将每个区组中的实验对象随机、均等地分配到各种实验处理中去[1].

1.3 随机区组设计的用途

用于随机区组设计的多个样本均数比较,其统计推断是推断各样本所代表的各总体均数是否相等.随机区组设计考虑了个体差异的影响,可分析处理因素和个体差异对实验效应的影响,所以又称两因素实验设计,比完全随机设计的检验效率高.该设计是将受试对象先按配比条件配成配伍组,每个配伍组有三个或三个以上受试对象,再按随机化原则分别将各配伍组中的受试对象分配到各个处理组.随机区组设计使用区组方法减小误差变异,即用区组方法分离出由无关变量引起的变异,使他不出现在处理效应和误差变异中[2～3].

2 随机区组设计的计算公式

随机区组设计的两因素方差分析是把总变异中的离均差平方和SS与自由度v分别分解成处理间、区组间和误差三部分,其计算公式见表1.

表1 方差分析的计算公式

3 实例分析

例某教师为了研究四种不同的写作训练方法中,哪种训练方法更有效,按照前一学期历次作文的成绩的平分数均将36名学生划分为优良、中等、一般三个写作水平,每个水平均有12名学生,而12名学生被随机均分到各实验处理.经一学期的写作训练后进行写作能力测试,计算出每一个学生的得分比前一学期历次作文平均分提高的分数,如表2.问四组教学方法的成绩提高幅度是否相同[1].

表2 研究数据表(成绩提高幅度)

本研究的主要目的在于比较教学方法的效果,同时还可以比较不同区组间学生成绩提高幅度是否相同.计算步骤为

步骤1方差齐性检验和正态性检验

因为Levene 统计量F(11,24)= 0.655,p= 0.765,所以不能拒绝原假设,认为方差齐;同时,Q-Q 图中(见图1)显示各点靠近各自的对角线,总体接近正态分布,可以做方差分析.

步骤2建立检验假设,确定检验水准

图1 Q-Q图

H0:各处理组学生成绩提高幅度相同,μ1=μ2=μ3=μ4;

H1:各处理组学生成绩提高幅度不同或不全相同,各μi不等或不全相等;

H0:各区组的成绩提高幅度相同;

H1:各区组的成绩提高幅度不同或不全相同.

步骤3计算各项平方和、自由度及均方

步骤4列方差分析表(如表3),进行F检验,确定P值并作出统计推断

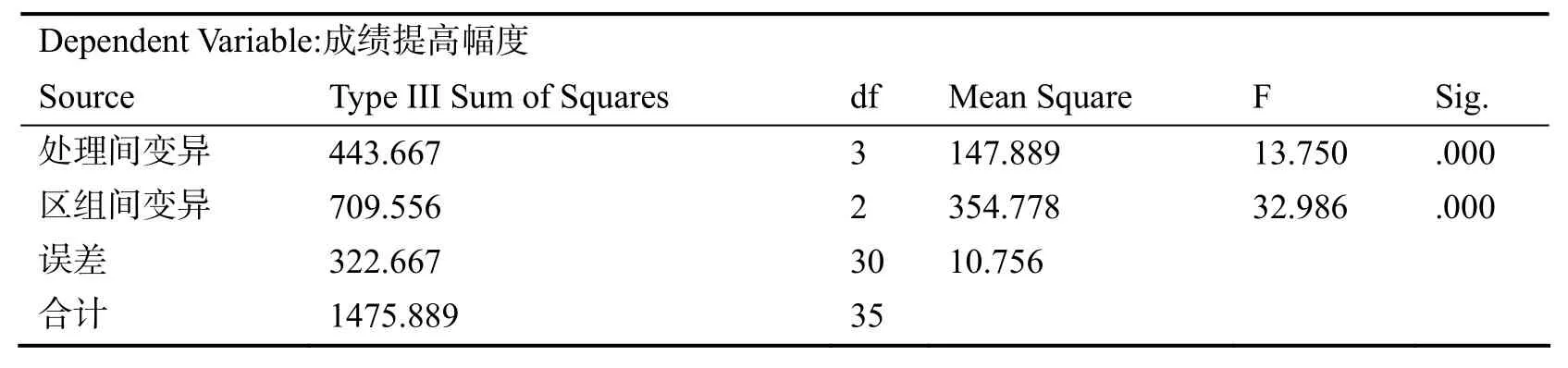
表3 例1的方差分析表Tests of Between-Subjects Effects

以v1=3,v2=30查F界值表,得F(0.05,3,30)=2.922277194,F(0.01,3,30)= 4 .50974,因为F(处理)＞F(0.05,3,30),F(处理)＞F(0.01,3,30),或因为p=.000＜0.01,按α=0.1水准,拒绝H0,支持H1,可认为各处理组学生的成绩提高幅度不同或不全相同,各处理间差异极显著,表明四种不同教学方法对学生的成绩提高幅度效果差异极显著,用不同的教学方法,提高幅度是不同的.如果要进一步推断任两个总体均数是否相同,应作两两比较[4].同理,可认为各区组学生的成绩提高幅度不同或不全相同,区组差异确实带来测量结果的变异,区组因素在本次实验中很重要,区组已经有利减少随机误差.

进一步,做 Tukey-Kramer (Tukey’s W)(最小显著极差的q法 )多重比较来确定哪些处理之间的平均数差异显著,哪些处理之间的平均数差异不显著[5].由表4,教学方法1、教学方法2、教学方法4与教学方法3两总体的均值存在显著差异.同时,两总体均值差的 95%置信区间没有跨 0,证实了以上推断:两总体均值存在显著差异;教学方法1、教学方法2、教学方法4两两之间总体的均值不存在显著差异.同时,两总体均值差的95%置信区间跨0,证实了以上推断:两总体均值不存在显著差异.

表4 多重比较表Multiple Comparisons

考察Tukey HSDa,b方法结果,均值为18.4444的组(教学方法3)与其它三组的均值有显著不同(其相似可能性小于0.05,被划分出来,形成两个相似子集.在第一个子集中,组内相似的可能大于0.05为0.105,第二个相似子集中,组内相似(自身相似)的概率为1.综上,可见第三种训练方法的效果最好.

表5 成绩提高幅度(相似子集)

图2 四种教学法成绩提高幅度箱形图

4 结语

文章阐述了单因素随机区组设计的方差分析的基本模式,运用随机区组设计的方差分析分析了四种教学方法对学生成绩提高幅度的差异性,研究发现:四种教学方法下学生成绩提高幅度不同或不全相同.经Tukey’s W检验的多重比较,教学方法2、教学方法1、教学方法4没有显著差异,教学方法2、教学方法1、教学方法4与教学方法3比较均显著差异,第三种教学方法的效果最好,其次是第每二教学方法.并给出了应用Mathematica[6]和SPSS做出的相关图形.

[1] 邓 铸,朱晓红.心理统计学与SPSS应用[M].上海:华东师范大学出版社,2009,(2):128～131

[2] 舒 华.心理与教育研究中的多因素实验设计[M].北京:北京师范大学出版社,2009:83

[3] 何晓群.多元统计分析[M].第3版.北京:中国人民大学出版社,2012

[4] Raghavarao,Damaraju and Padgett,L.V.Block Designs:Analysis,Combinatorics and Applications[M].World Scientific,2005

[5] 杨厚学.应用统计分析[M].成都:西南交通大学出版社,2009

[6] Stephen Wolfram.The Mathematica Book[M].5th ed.Wolfram Media,2003