喷射GFRP加固砖墙抗剪承载力有限元分析★
张 智 谷 倩 余启明
(1.武汉工业学院土木工程与建筑学院,湖北武汉 430023;2.武汉理工大学土木工程与建筑学院,湖北武汉 430070)
玻璃纤维聚合物(GFRP)是由玻璃纤维和树脂共同组成的复合材料,将其应用于结构加固补强具有高强高效、耐腐蚀性好、施工方便和适用面广等优点。目前,国内外有关GFRP纤维织物或片材缠绕粘贴加固砌体结构的研究已取得较多成果,但采用喷射GFRP加固补强技术加固砌体结构的研究近几年才刚刚起步[1]。为验证试验结果的合理性,本文采用ANSYS有限元分析方法对喷射玻璃纤维聚合物加固带构造柱砖墙进行了数值研究,着重介绍了加固对墙体承载力的影响,并与试验结果进行对比分析。
1 试验研究
1.1 试件及加固
试验共制作4片带构造柱墙片,其中一片未加固试件为对比试件,另3片均喷射玻璃纤维聚合物加固,制作试件的材料为MU10蒸压粉煤灰砖和M5的混合砂浆,试件尺寸如图1所示。砌筑严格按照砌体基本力学性能实验方法标准进行。试件编号及加固方案如表1所示,试验喷射成型的GFRP性能指标如表2所示[2]。
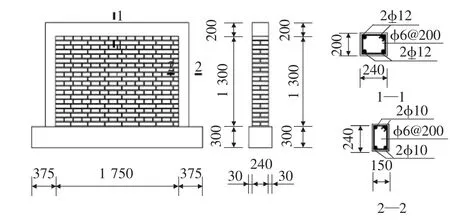
图1 试件尺寸图

表1 试件编号及加固方案

表2 喷射GFRP的性能指标
1.2 试验结果
试验装置为常规拟静力装置,试件的加载制度采用先控制作用力,后控制位移的混合加载法[3]。水平位移由墙体最上一皮砖中部布置的位移计采集,经动态电阻应变仪收集后输出到函数记录仪,与由往复作动器前端的拉压力传感器采集的荷载数据结合,可绘制试验过程中试件的滞回曲线,滞回曲线的外包线称为骨架曲线,能直接反映加载过程中荷载与位移之间的关系,试件的骨架曲线如图2所示。
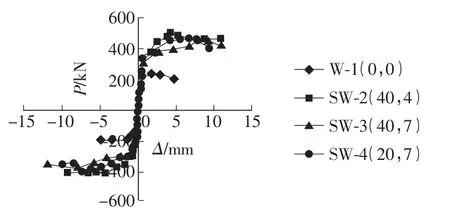
图2 各试件的骨架曲线
由试验实测所得的滞回曲线分析可得承载力结果如表3所示。
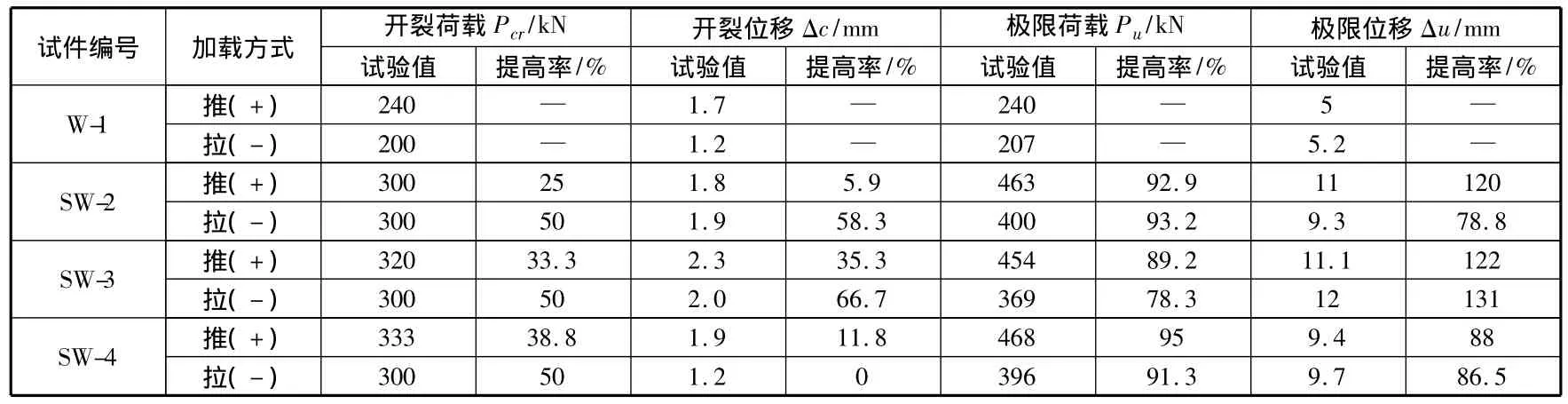
表3 试件试验结果
从表3可以看出,相对于对比试件W-1,3片经过喷射GFRP加固墙体的开裂荷载和极限荷载均有较大的提高。对比试件SW-2和SW-3(相同的纤维长度,不同的喷射厚度),二者的开裂荷载和极限荷载的提高率比较接近,可以认为,喷射GFRP厚度对加固墙体抗剪承载力的影响并不大;对比试件SW-3和SW-4(相同的喷射厚度,不同的纤维长度),SW-4的开裂荷载和极限荷载均比SW-3的稍大,可见,纤维长度对墙体的抗剪承载力有一定影响,纤维越短,承载力越大。但是,SW-4的开裂位移和极限位移提高率都要小于SW-3,长纤维更有利于提高墙体的变形能力。
2 ANSYS有限元模型
考虑到砌体结构模型复杂性,本文中采用分离式建模。为使模型更接近于实际,采用自由网格划分,利用人工设置智能尺寸控制技术(SMARTSIZE命令)来自动控制网格的大小和疏密,在体上自动生成四面体网格[4]。为模拟试验中地梁被完全固定的约束情况,ANSYS分析时,将地梁底部简化为固定支座,三个方向的自由度均被约束。
荷载可以分为两部分,一部分为在顶梁上表面施加Z方向的面荷载,荷载值为0.4 MPa,另一部分为水平低周往复荷载,采用X正反两方向逐级增大荷载。建立的ANSYS有限元模型如图3所示。
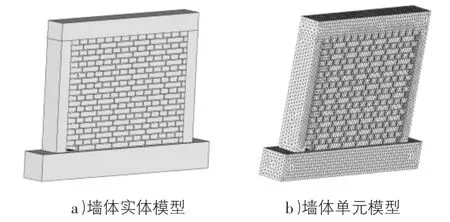
图3 墙体有限元模型
3 对比分析
3.1 模型 W-1
ANSYS计算和试验实测得到的对比试件W-1的荷载—位移曲线如图4所示。
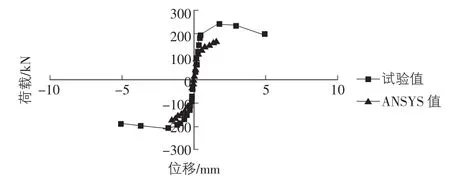
图4 W-1荷载—位移曲线
从图4中可以看出,在加载的初期,ANSYS计算的荷载—位移曲线与试验值吻合较好,在荷载超过115 kN后,ANSYS模型W-1的荷载—位移曲线斜率变大,此时模型进入弹塑性阶段。ANSYS有限元计算得到的极限荷载小于试验实测得到的实际极限荷载,主要原因是在实际加载过程中,当出现局部破坏时,试件并不会马上丧失承载能力,能在一个较大的范围内继续承担不断增大的荷载;但ANSYS数值计算与实际情况并不一样,一旦出现了局部应力过大,变形过大,本文实体模型较为复杂的网格划分使得单元有可能出现畸变,计算无法继续进行,最终造成无法收敛,计算终止。ANSYS计算得出的极限位移相比试验实测值小了很多,其主要原因是没有考虑砂浆与砖块之间的粘结滑移,试验试件的刚度退化速度明显快于ANSYS模型;从计算结果可以看出,运用ANSYS进行有限元分析很难模拟荷载—位移曲线的下降段。
3.2 模型 SW-2
ANSYS计算和试验实测得到的模型SW-2的荷载—位移曲线如图5所示。
从图5中可以看出,相比于对比模型W-1,模型SW-2极限荷载和极限位移均有较大幅度的提高,分别为达到387 kN和4.05 mm,但与试件W-1类似,ANSYS有限元计算的极限承载力和极限位移均小于试验值。当荷载小于175 kN时,墙体尚未开裂,此时模型处于弹性阶段,荷载—位移曲线接近于直线,当荷载达到约175 kN时,由于墙体出现裂缝,模型整体刚度有所退化,荷载—位移曲线的斜率变小。
3.3 模型 SW-3
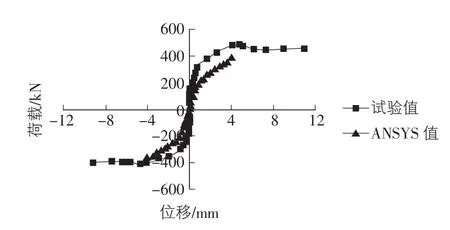
图5 SW-2荷载—位移曲线
ANSYS计算和试验实测得到的模型SW-3的荷载—位移曲线如图6所示。
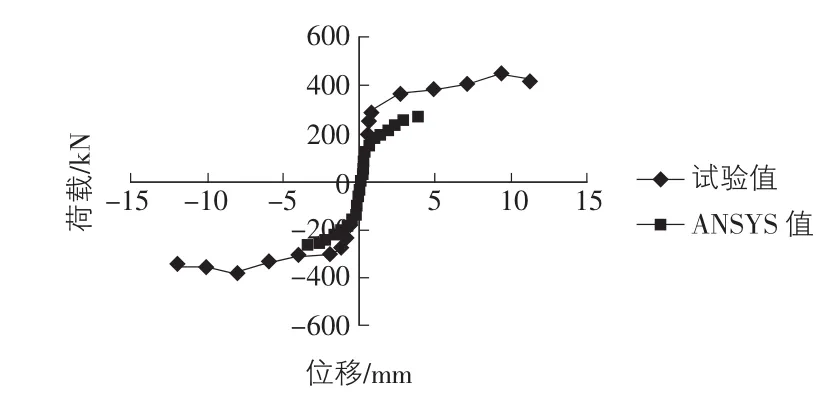
图6 SW-3荷载—位移曲线
从图6中可以看出,相比于对比模型W-1,模型SW-3极限荷载和极限位移也有一定程度的提高,分别为达到276 kN和3.78 mm,但与试件W-1类似,ANSYS有限元计算的极限承载力和极限位移均小于试验值。当荷载小于165 kN时,墙体尚未开裂,此时模型处于弹性阶段,荷载—位移曲线接近于直线,当荷载达到约165 kN时,由于墙体出现裂缝,模型整体刚度出现退化。
3.4 模型 SW-4
ANSYS计算和试验实测得到的模型SW-4的荷载—位移曲线如图7所示。
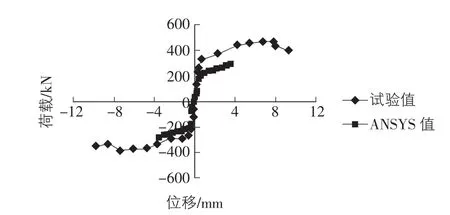
图7 SW-4荷载—位移曲线
相比于对比模型W-1,由ANSYS有限元计算得的SW-4的极限荷载和极限位移也有一定程度的提高,分别为达到293 kN和3.49 mm。相比于模型SW-3,承载力有所增大而变形能力却降低了,这与试验结果是一致的,较短的玻璃纤维长度能更有效提高结构的承载能力,但玻璃纤维越长对提高结构的变形能力越有效。
4 结语
1)有限元分析结果表明,喷射GFRP加固能显著提高模型的极限荷载和极限位移,较短的玻璃纤维长度能更有效提高结构的承载能力,但玻璃纤维越长对提高结构的变形能力越有效。这与试验结果是一致的。2)试验时,当出现局部破坏时,由于结构的整体作用,试件并不会马上丧失承载能力,能在一个较大的范围内继续承担不断增大的荷载;而在ANSYS数值计算时,当出现了局部应力和变形过大,单元就有可能出现畸变而无法收敛,计算无法继续进行,因此有限元计算得出的极限荷载均小于试验值。3)由于未考虑砂浆与砖块、加固层与墙体之间的粘结滑移,有限元模拟计算得出的变形远小于墙体的实际变形。4)有限元分析时仅在顶梁上表面施加0.4 MPa的均布竖向荷载,并未施加约束,但在试验时,施加竖向荷载的反力横梁和反力架实际上对墙体在Z方向起到了一定的约束作用,对提高墙体的抗剪承载力也起到一定的效果。
[1] 张 智,谷 倩,霍凯成.喷射玻璃纤维聚合物加固砖墙试验研究[J].武汉理工大学学报(自然科学版),2010,32(13):58-61.
[2] A.J.Boyd.Rehabilitation of Reinforced Concrete Beams with Sprayed Glass Fiber Reinforced Polymers[D].Vancouver,BC:The University of British Columbia,2000.
[3] JG 101-96,建筑抗震试验方法规程[S].
[4] 郝文化.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2005.

