基于内核的低秩逼近算法的改进

高 超

(哈尔滨工程大学信息与通信工程学院，哈尔滨150001)

分析、提取和处理数据集的几何结构在数据挖掘中占有重要的地位[1].多数情况下，数据集(如文本数据集)的结构是非线性的，或者数据集的运算可能不具有线性运算的特点.此时，非线性特征更能反映数据集的特性[2].低秩逼近技术是解决非线性模式分析问题的有效途径之一.文献[3]提出了一种较有代表性的方法，基于低秩逼近技术的内核算法(KBLA).它从原数据矩阵中非均匀地抽取一个小的样本矩阵，再用与原数据矩阵相关的概率分布函数处理该样本矩阵，接下来构建一个可用于逼近原数据矩阵的秩为k的小块矩阵，最后用此小块矩阵逼近原数据矩阵.

虽然该算法在一定程度上可以较好的逼近原数据矩阵，但是该算法的逼近精度还有待提高.本文通过对原始矩阵的每一列赋予一个概率，并抽取概率最大的前c列构成样本矩阵，接下来用此样本矩阵生成小块逼近矩阵，以提高逼近精度.

1 改进的基于内核的低秩逼近算法

定义1 假设W∈ℝn×n是对称半正定矩阵，W(i)表示矩阵W的第i列，与W的列相关的概率分布函数 pi用下式表示，

定义2 权值矩阵D:D∈ℝc×c，是一个对角矩阵，对角线上的元素服从与矩阵列相关的非均匀分布，且其值依次递减，

其中:pt表示在第t次独立随机试验中第 t次的概率.

定义3 采样矩阵S:S∈ℝc×c，是一个由数字0和1组成的矩阵，且它的每列只有一个元素是1，其余元素是0.它的前c行也具有相同的特征.后n-c行构成全零矩阵.在对矩阵A的列向量进行c次独立随机抽样试验时，如果在第j次抽样试验中，

记，n×c矩阵C=WSD为经过赋权值后的，从矩阵W中按非均匀概率分布函数抽取的列向量构成的矩阵.再记，c×c方阵=(SD)TWSD为经过赋权值后的，从矩阵W中抽取的列标签和行标签相交的元素构成的矩阵.

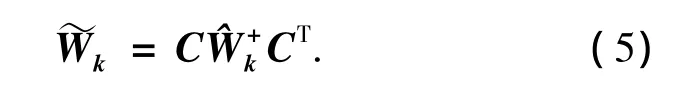
具体的算法实现步骤如下.

输入:数据 A∈ℝn×p，采样点数 c，尺度因子 t.

1)根据数据集A建立相似度矩阵W;

2)分别利用式(1)，(2)和(3)计算概率分布函数pi、对角矩阵D和抽样矩阵S;

2 误差分析

定理1[4](标准 Nyström 方法)在上述假设条件下，对任意的c，δ＞0，以下不等式成立的概率至少是1-δ，

定理2[3](KBLA)在上述假设条件下，如果存在概率分布函数pi，使得

那么，当 c≥64kη2/ε4，η =1+(8log(1/δ))1/2，时，对任意的ε＞0，不等式以至少1-δ的概率成立，

IKBLA算法的逼近误差的上界与KBLA的相同，其推导过程与定理2的相同，在此，不再给出(参见文献[3]的定理3).从上述2个定理可知，基于低秩逼近技术的KBLA和IKBLA算法的逼近误差的上界比标准Nyström方法的逼近误差的上界小得多.

3 实验设计与结果分析

为了验证IKBLA的有效性，本文将之与三种逼近算法进行了比较.在UCI数据库中部分数据集上的实验结果验证了算法的有效性.

实验环境:硬件环境，CPU Intel Core 2 Quad Q6600 2.4G，Internal memory 4G，Hard disk Hitachi HDP 725050GLA360 500G.软件环境，Windows 2003+Matlab2007b.

3.1 实验数据集描述

在表1的描述中，Sonar，H.S，L.D，L.M，P.I.D，C.M.C，I.S，W.D.G 分别是如下数据集的缩 写，ConnectionistBench (Sonar， Minesvs.Rocks)，Haberman’s Survival，Liver Disorders，Libras Movement，Pima Indians Diabetes，Contraceptive Method Choice，Image Segmentation，Waveform Database Generator(Version 1).

表1 实验数据集描述

3.2 实验方法的参数设置及评价指标

以下是实验中用到的几种方法及其参数设置.

利用Nyström方法的谱聚类(NS):是文献[5]提出的方法.只执行NS的逼近程序不执行聚类程序.高斯核的尺度因子 t为0.5，采样点数 c为50个.

基于Nyström的核方法(NBKM):是文献[6-7]提出的逼近方法.采用服从均匀分布的概率分布函数计算矩阵D.参数设置同上.

KBLA:是文献[3]提出的逼近算法.与NBKM算法的惟一区别是采用式(7)计算矩阵D.参数设置同上.

IKBLA:本文提出的算法.与KBLA算法的区别是IKBLA采用式(1)和(2)计算矩阵D.参数设置同上.

误差E的计算方法为，

3.3 实验结果与分析

本文将上述四种算法在表1描述的数据集上进行了测试.所得的逼近误差E如表2所示.每次实验产生的最小逼近误差E用“粗体+下划线”标出.

表2 四种算法的逼近误差E

表2指出，NS的逼近误差最大，其值大致分布在104～106之间.这一点与定理1的结论吻合.IKBLA，NBKM和KBLA的逼近误差均比NS的小得多，值大致分布在102～103之间.这表明在用小块采样矩阵恢复大块原数据矩阵的过程中，不宜用基于Nyström采样技术的 NS.比较 KBLA和 NBKM的逼近误差.数据显示两者的逼近误差不相上下.这说明在声呐、图像和波浪等数据集上，与原数据矩阵所有列向量相关的，在数值上无规律可循的，服从非均匀分布的，概率分布函数的引入几乎没有改善低秩逼近算法的性能.再分别比较IKBLA和NBKM，IKBLA和KBLA的逼近误差.可以看到IKBLA取得了最低的逼近误差.这是因为所选的c个代表点与剩余点间的关系更密切，更能反映数据集的特性.也表明同样是服从非均匀分布的，但在数值上呈现递减规律的，概率分布函数的引入在一定程度上改善了低秩逼近算法的性能.综上所述，IKBLA可以被有效地应用于UCI中部分数据集的逼近中.

4 结语

针对KBLA的逼近精度还有待提高的问题，本文提出了一种改进的低秩逼近算法.用在数值上呈递减规律的，非均匀概率分布函数取代在数值上无规律可循的非均匀概率分布函数，使低秩逼近技术的逼近精度进一步的提高.算法在UCI数据库中部分数据集上取得的实验结果验证了它的有效性.

[1]TAN P N，STEINBACH M，KUMAR V.Introduction to Data Mining[M].USA:Addison Wesley，2005.

[2]史卫亚.大规模数据集下核方法的技术研究[D].上海:复旦大学，2008:5-9.

[3]DRINEAS P，MAHONEY M W.On the nyström method for approximating a gram matrix for improved kernel-based learning[J].Journal of Machine Learning Research，2005，6:2153-2175.

[4]KUMAR S，MOHRI M，TALWALKAR A.Ensemble nyström method[C]//23rd Conference on Neural Information Processing Systems，Vancouver，BC，Canada:The MIT Press，2009，1060-1068.

[5]FOWLKES C，BELONGIE S，FAN C，et al.Spectral grouping using the nyström method[J].IEEE Trans.Pattern Anal.Mach.Intell.，2004，26(2):214-225.

[6]WILLIAMS C，SEEGER M.Using the nyström method to speed up kernel machines[C]//Proceedings of the 2000 Conference on Advances in Neural Information Processing Systems，Chicago，USA:The MIT Press，2001:682-688.

[7]李万臣，高毓亮，齐 欢.基于LIE-QC结构的速率兼容LDPC码优化构造方法[J].哈尔滨商业大学学报:自然科学版，2012，28(5):546-550.