恶劣天气影响下动态改航策略研究

张晨靓，田 勇

(南京航空航天大学民航学院，南京210016)

近年来，随着我国民航运输业的飞速发展，空中交通流量的迅速增长，现有的空域结构、网络布局、通信导设施等难以适应现代空中交通流量增长的节奏，在机场、终端区及航路交叉点等处飞行冲突和拥挤现象频繁发生，航班延误日益增多.实施空中交通流量管理是减少航班延误成本的重要手段，目前空中交通流量管理采取的主要措施是对未起飞的航班采取地面等待，对已经起飞的航班采取空中等待或者改航.地面等待策略的实质是将昂贵的空中等待“吸收”转化为相对低廉的地面等待，以达到延误成本最优化的目的.改航亦是空中交通流量管理的重要组成部分，在空中交通系统中，空域单元往往受各种实际因素的影响(恶劣天气、军航活动、重大事件等)，造成可用时空资源与服务能力下降，从而对航空运输造成不可估量的损失，改航策略旨在空域受限或管制服务能力下降时，实施改航策略以避让受限单元，从而保证空中交通安全有序畅通的运行.

改航策略的研究始于1993年，经过近20年的探究，国内外学者对改航策略的研究已经取得了很大的成果.其中具有代表性的有:1997年，Sarah Stock Patterson建立了改航的数学模型，并用拉格朗日算法进行了求解[1].2002年宋柯在 Sarah Stock Patterson建立的模型的基础上提出了基于已有网络流的航路点A*搜索算法[2].2004年Jimmy Krozel等人提出了基于自由飞行的改航路径规划方法[3].2007年，叶志坚对静态雷雨天气下的改航路径进行了研究[4].2008年田勇等人以全国范围的航班时刻表数据和天气数据为例对改航进行仿真验证[5].2010年万莉莉等人进行了基于多目标优化的改航策略研究，把地面等待与改航策略相结合，对改航策略进一步优化，减少了成本，提高了改航效率[6－7].

前期学者主要提出了航路改航的基本模型，并着重研究了改航路径的优化方法，其中对改航策略与其他流量管理策略的综合运用也取得了一定的研究成果，但改航模型中改航决策都是静态的，未能根据实时的天气信息做出动态调整.本文提出了一个整数线性规划模型，主要研究恶劣天气影响下航班动态改航方法，当恶劣天气影响原计划进场航路导致航路容量下降时使航空器改航到其他进场航路进场着陆.其中地面等待策略是在航班起飞前做出的，空中等待和改航是根据实时的天气信息而决定的.

1 情景树

情景树是多阶段决策中使用的一种的方法，常用于金融投资决策，它的优点是形象直观.一般“情景树”的图示包括节点和连线，图1为一个二阶段的“情景树”，根节点A0为初始状态，此时所有的信息都是已知的.根节点的三个分支分别代表在 t=1时刻的三种可能的状态，即B1，B2，B3，其概率分别为 p1，p2，p3且满足条件 p1+p2+p2=1.在未来t=2时刻，B1亦有两个后继节点分别表示两种可能的状态C11和C12，发生的概率分别为p11，p12同样满足条件p11+p12=1.在一棵“情景树”中，有一个惟一的父节点(根节点)，众多的子节点，每个子节点可以拥有一个或若干个后继节点，情景树中每一条路径代表一个情景，如图1所示，A0－B1－C11构成的路径表示一个具体的情景Q，其发生的概率为 p1·p11.

在动态最优化模型求解过程中，情景树可以表示航路容量变化的不确定性，改航模型中的改航决策可以在分支处进行调整，因此将情景树运用于动态改航策略之中，其中t=0时刻从各个机场起飞经过相同航路点到达同一目的地机场的航班数量是已知的，这就相当于情景树中的父节点A0.若连接某两个航路点之间的航路受到恶劣天气影响则航班需选择一条合适的飞行路径绕飞以避开恶劣天气的影响，在t=1，2…T时刻，航班到达航路点时恶劣天气可能会消散，若恶劣天气消散航班就可按原计划航路飞行，这就相当于情景树中的各子节点.假设共有n个情景，若恶劣天气在t=1时刻消散则将此情景记为1，若恶劣天气在t=2时刻消散则将此情景记为2，依次类推，用pQ表示各个情景发生的概率，Q∈{1，2，…n}.

图1 情景树示意图

2 动态改航模型

2.1 问题描述

飞机飞行过程一般来说按航路点飞行，飞机脱离航路后必须按照规定的高度进入空中走廊口，空中走廊飞行结束后飞机按标准仪表进场航线飞向起始进近定位点IAF并开始进近飞行，最后着陆滑跑脱离跑道.

假设连接走廊口与目的地机场之间的航路受到恶劣天气影响容量降低为零，设走廊口为改航起始定位点，记为K，目的地机场为改航结束定位点，对于改航定位点K存在一条的最短的备选航路飞往目的地机场，一旦某架航班f通过改航定位点K选择备选航路飞往目的地机场，则此后这架航班f不允许再进行航路的更改.用r1表示航班按原计划航路飞往目的地机场，r2表示航班选择备选航路飞往目的地机场.Km(t)表示从不同机场起飞在时间片t∈Γ之前计划到达改航定位点K的累积航班数量，Γ={1，…，T}表示相等的时间间隔l的集合，Km(t)的取值可以从相应的航班计划时刻表中获得.将目的地机场在t时间片内的航班进场容量表示为Ck(t)，其进场容量为考虑从其他方向进场的航班在相同的时间片t内进近着陆后剩余的容量值.λ1表示航班f从改航点K按原计划航路飞往目的机场所用的时间，λ2表示航班f从改航点K选择备选航路飞往目的机场所用的时间，λ2－λ1表示航班选择备选航路飞行的额外飞行时间.值得注意的是:上述额外飞行时间λ2－λ1须能整除时间间隔l，整除的倍数记为n.

本文主要考虑目的地机场进场容量的限制，不考虑连接改航定位点和目的地机场之间的其他航路点容量限制，即所有通过改航点K的航班都能顺畅进近着陆，航班可以在改航点处进行空中等待，等待的原因可能是由于进场容量限制，也可能是在改航决策之前等待关于天气情况的进一步信息.

2.2 决策变量

用Xm(t)表示在时间片t之前到达改航点K累积航班数量;YmQ(t)表示在情景Q下，时间片t之前通过改航点K的累积航班数量;ZmQri(t)，i=1，2表示在情景Q下，时间片t之前选择航路ri飞往目的地机场的累积航班数量;SmQri(t+λi)表示在情景Q下，时间片t+λi之前到达目的地机场的累积航班数量;

由上述决策变量可得在时间段内各个起飞机场航班的地面等待“累积总量”为:

航班通过改航点K之前可能会进行空中等待，在情景Q下时间片t内在改航点K空中等待量可由如下公式计算得到:

在情景Q下时间段内，航班因改航而增加的额外飞行时间Δt为:

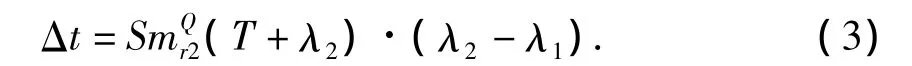
2.3 目标函数及约束条件

目标函数是使总延误成本最小，表达式如下:

上式中右边第1项为在时间片T之前所有航班因采用地面等待所产生的延误总成本，第2项为在时间片T之前所有航班进行空中等待所产生的延误总成本，第3项为时间片T之前所有航班因改航而增加的额外飞行总成本，其中gc和ac分别为航班在地面和空中等待单位时间所消耗的成本，l为航班平均地面等待和空中等待时间，若某架航班没有在相应的时间片内到达或通过改航点，则认为这架航班在地面、空中等待了一个时间间隔l，考虑我国是以5 min为一个基本单位计划航班的起飞时刻的，因此本文中时间间隔l取值为5 min.

以下为一系列的约束条件:

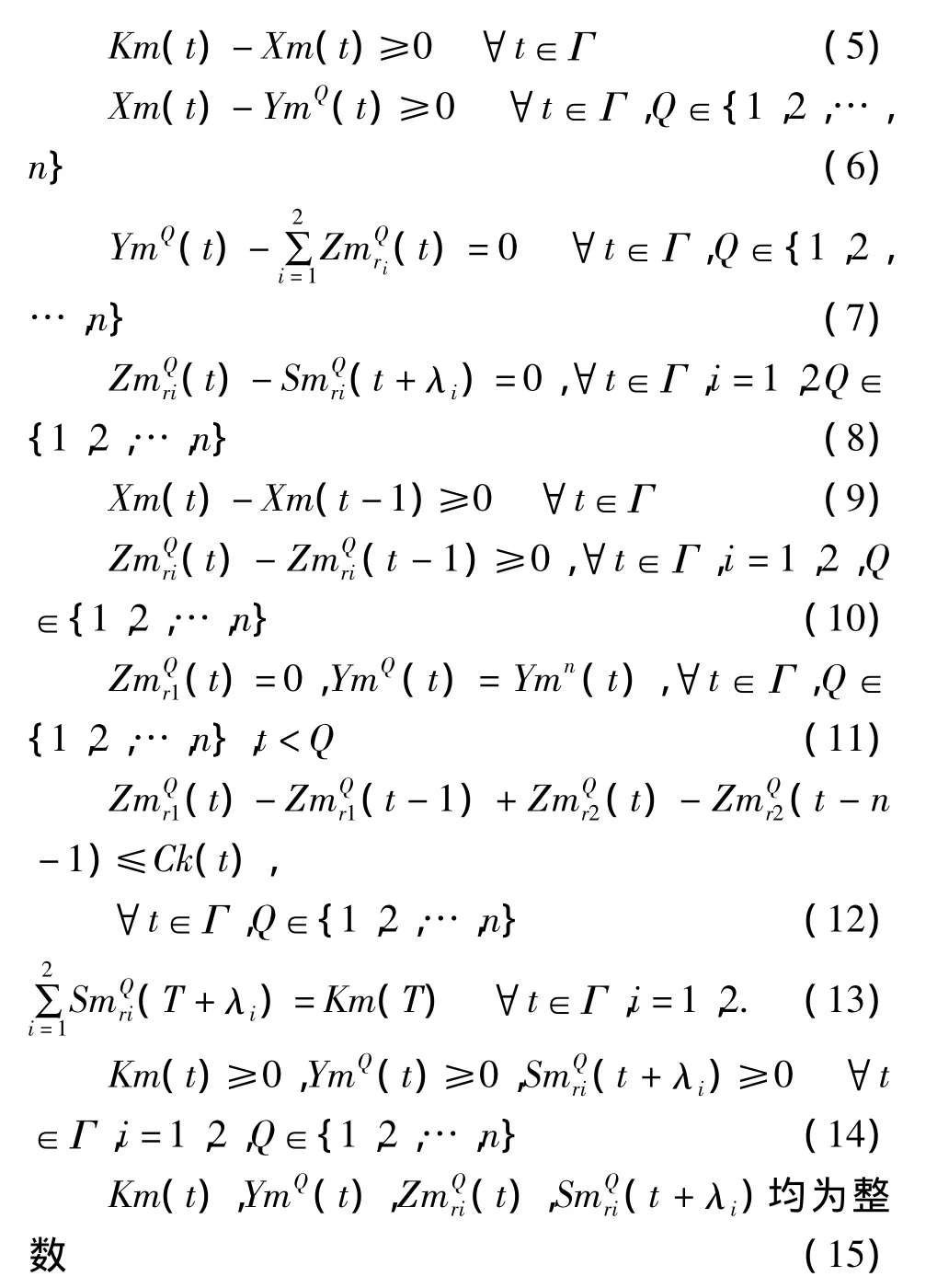
式(5)表示所有航班都不能早于原计划起飞时间提前起飞;式(6)表示在时间片t之前通过改航点K的累积航班数量不能超过到达改航点K的累积航班数量;式(7)表示在时间片t之前选择不同的航路ri飞往目的地机场的累积航班数量之和等于通过改航点K的累积航班数量;式(8)表示在时间片t之前通过改航点并选择航路ri飞行的航班都会在时间片t+λi之前到达目的地机场;式(9)、(10)表示所有决策变量均是递增的，即航班到达改航点、通过改航点选择不同的航路飞行到达目的地机场的航班数量是累加的;式(11)表示若时间片t+1之前航路上恶劣天气没有消散则航班不能选择此航路飞行，且时间片t+1之前通过改航点的累积航班数量是以时间片t之前通过改航点的累积航班数量为基础的;式(12)表示时间片内按原计划航路飞行到达目的地机场的航班数量与时间片(t－n)内改航到达目的地机场的航班数量之和不大于时间片内目的地机场的进场容量;式(13)表示没有航班取消，所有航班都可以在T+λi之前着陆;式(14)、(15)表示所有的决策变量均为正整数.

3 算例分析

将动态改航模型应用于上海虹桥国际机场(ZSSS)，从上海虹桥机场的西南方向例如昆明、长沙、汕头、深圳等城市飞来的航班经常通过庵东(AND)经航路G204飞行到达上海虹桥国际机场.若航路G204受到恶劣天气影响，从庵东进场的航班可以改航从走廊口无锡(VMB)进场到达上海虹桥机场，将庵东作为改航定位点K.标准仪表进场航路如图2所示，图中虚线表示航班按原计划航路飞行达到虹桥机场，实线表示航班选择备选航路飞行达到虹桥机场.根据庵东、南浔(NXD)、无锡定位点的经纬度坐标，由大圆航线计算可得从庵东到南浔、南浔到无锡的距离分别为104、78 km.假设航空器的巡航速度为0.7马赫，考虑到航空器进入无锡走廊口最大飞行速度，可得航班从庵东飞行到达无锡的时间为15 min.同理可知航班从无锡进场飞行到达上海虹桥机场的时间为20 min，从庵东进场飞行到达上海虹桥机场的时间为15 min.因此航班从无锡走廊口改航进近的额外飞行时间为20 min.假设在良好天气条件下每小时上海虹桥国际机场进场最大容量为48架，则5 min内虹桥机场最大进场容量为4架.

图2 上海虹桥国际机场进场示意图

如图2所示，航路G204上午7:00～9:00受到恶劣天气影响容量降低为0，由卫星云图分析可知航路G204会在上午9:00～10:00内放晴，同时考虑到10:00～10:20这一时间段，以5 min为1个基本单位将时间段9:00～10:20划分为16个时间片、13个情景，假设每个情景发生的概率都相等.结合实际情况，选取上海虹桥机场2012年某日9:15～10:35的实际数据，时间段9:15～10:35内从庵东方向和从其它方向进场(无锡方向)的进场的航班计划时刻表分别如表1、2所示.空中等待成本等于地面等待成本和燃油成本之和[8－9]，本实验中取空中等待与地面等待的成本比例系数为3，设gc=b元/min，则 ac=3b元/min.

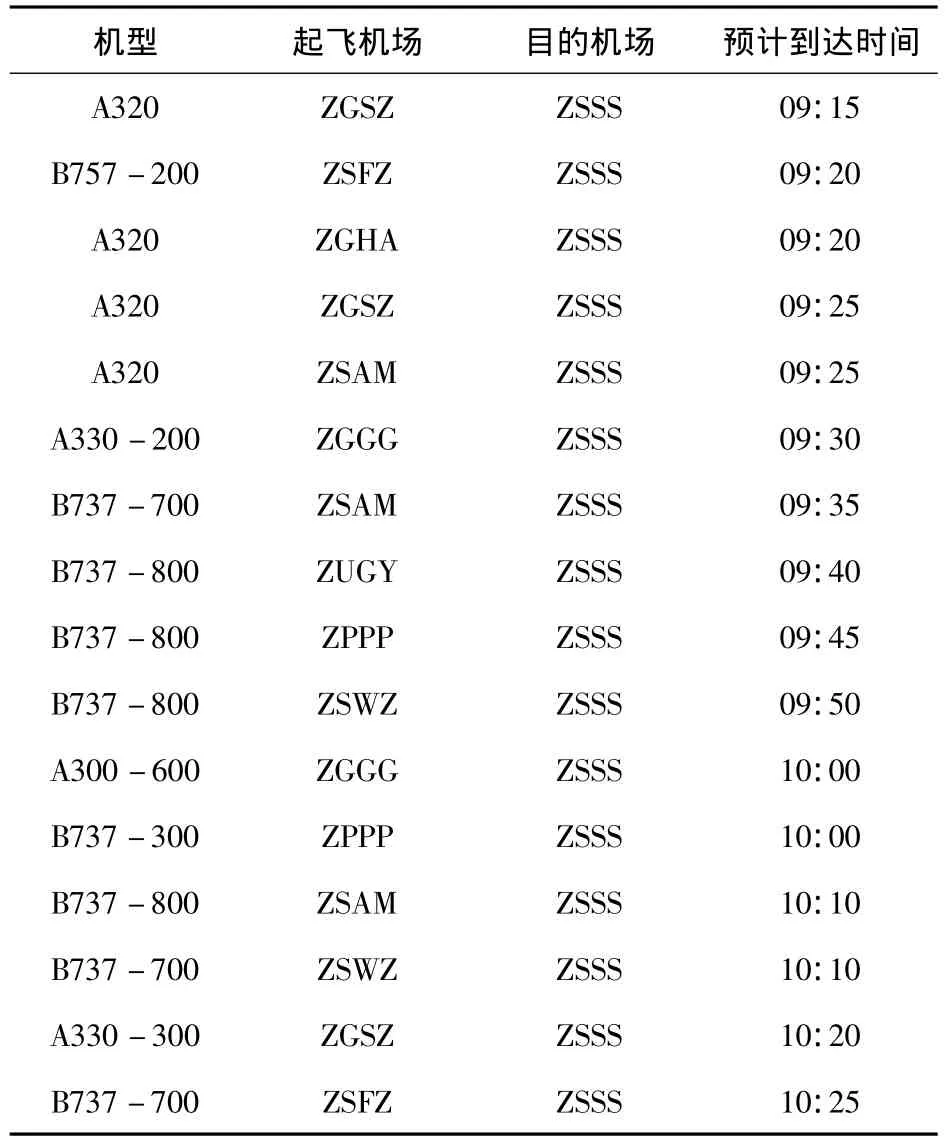
表1 9∶15～10∶35从庵东方向进场的航班计划时刻表

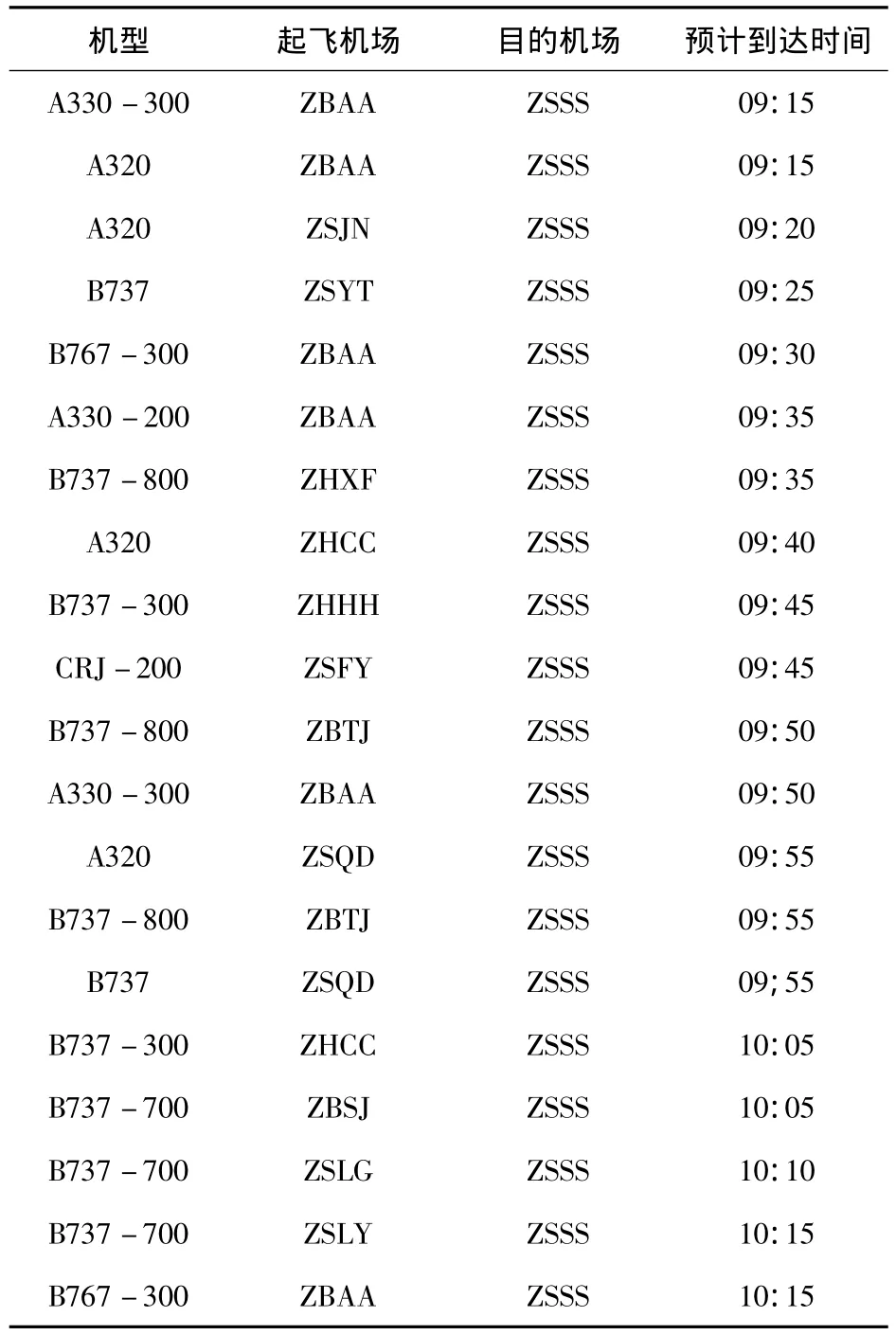
表2 9∶15～10∶35从无锡方向进场的航班计划时刻表

本文所建立的动态改航模型为整数线性模型，当问题的规模比较大时，枚举法的计算量就难以接受，Lingo是在整数线性规划中常用的方法和程序.Lingo中建立的优化模型由五个部分组成:集合段(SETS)、目标与约束段、数据段(DATA)、初始段(INIT)、计算段(CALC).其中计算段可以对一些原始数据进行计算处理，在实际问题中，输入的数据通常是原始数据，不一定能在模型中直接使用，因此在这个段对这些原始数据进行一定的“预处理”，就可以得到模型中真正需要的数据.在本算例中对从无锡方向进场的航班进行预处理就可以得到各个时间片虹桥机场的进场容量Ck(t)，对G204航路的容量进行预处理就可以模拟情景树中各情景下航路容量随时间的变化.

根据上述数据采用Lingo11软件对动态改航模型进行编程求解，变量562个、约束1136个、迭代438次、耗时1 s求得恶劣天气影响下动态改航最小总延误成本为425.4元，同时得到各时间片之前到达庵东的最佳累积航班数量分别为:1、3、4、6、7、8、9、9、9、12、12、14、14、15、16、16 架.

将动态改航策略的总延误成本分别与静态改航策略和地面等待策略的总延误成本进行对比，相比静态改航策略减少了延误成本189.6元，约为静态改航策略总延误成本的30.83%，相比于单一的采用地面等待策略减少了延误成本269.6元，约为地面等待策略总延误成本的38.79%.

4 结语

本文提出了一个整数线性规划模型，对恶劣天气影响下的动态改航方法进行了深入研究，该模型以总延误成本最小为目标，综合考虑了地面等待、空中等待和改航策略.通过对上海虹桥国际机场上午9∶15～10∶35时间段内从庵东进场的航班进行分析得出了各各时间片之前到达改航点最佳累积航班数量.结果表明:在航路受到恶劣天气影响时，采用动态改航策略可以更加有效的利用空域资源，减少航班延误成本.

动态改航还可以进行更深一步研究，动态改航模型的决策变量是计划到达各航路点的航班数量而不是直接给每个航空器分配到达时间，动态改航求得的结果可以运用类似RBS的资源分配算法给每个航班分配放行和到达时间.

[1]PATTERSON S S.Dynamic Flow Management Problems in Air Transportation[D].US:Massachusetts Institute of Technology，1997:55－76.

[2]宋 柯.空中交通流量管理改航策略初步研究[D].南京:南京航空航天大学，2002.

[3]KROZEL J，STEVE P，JOSEPH P，et al.Comparison of algorithm s for synthesizing weather avoidance routes in transition airspace[C]//In Proceedings of the AIAA Guidance，Navigation，and Control Conference，Providence，RI，2004，:1 －16.

[4]叶志坚，戴福青，杨新湦.避免雷雨天气的航路选择方法[C]//第七届全国交通运输领域青年学术会议，天津，2007:1126－1134.

[5]田 勇，宋 柯，顾英豪.空中交通流量管理中的改航策略研究[J].数学的实践与认识，2008，38(10):70 －76.

[6]万莉莉，田 勇，叶博嘉.基于多目标优化的改航策略研究[J].数学的实践与认识，2010，40(22):99 －106.

[7]朱金福.航空运输规划[M].西安:西北工业大学出版社，2009.

[8]李 雄.飞行危险天气下的航班改行路径规划研究[D].南京:南京航空航天大学，2009.

[9]张 慧，韩松臣.基于灰色重力模型的终端区空域流量分布预测[J].哈尔滨商业大学学报:自然科学版，2010，26(1):38－41.