一种基于超立方体图的Hadamard矩阵构造法

王 岚 王敏峯

（1.福建广播电视大学 计算机系，福建 福州350003；2.中国人民大学 信息学院，北京 100872）

1引言

1867年，英国数学家詹姆斯·约瑟夫·西尔维斯特从正交性思想出发，提出了Hadamard矩阵[1]，至今已经有一百多年的历史。由于Hadamard矩阵具有优良的正交特性，使得它在区组设计[2]、数据压缩[3]、数字图象处理[4]、数据挖掘[5]、信息安全[6]、通信理论[7]、量子计算[8]、编码理论[9]等诸多领域有着重要的应用。

2 Hadamard矩阵的构造问题

首先给出Hadamard矩阵的定义[10][11]：

定义1 设Hn为一个完全以+1与-1为元素的n×n方阵，如果H满足：

则称Hn为一个n阶Hadamard矩阵。

对于给定的阶数n，若要判断n阶Hadamard矩阵是否存在，可根据如下定理[11]：

定理1 n阶Hadamard矩阵存在的必要条件为：n为自然数，并且满足：

或者

所谓的Hadamard矩阵构造问题即要求寻找到符合上述必要条件的任意阶Hadamard矩阵的构造方法。针对这一问题，几十年来许多学者提出各种各样的解决办法，其中较为著名的有Sylvester构造法[1]、Paley 第一构造法[12]、Paley 第二构造法[12]、Williamson构造法[13]、Turyn 构造法[14]、强直积构造法[14]等等。

尽管已经提出了许多种Hadamard矩阵构造方法，但是，Hadamard矩阵的构造问题仍未完全解决，有许多指定阶数的Hadamard矩阵至今找不到构造方法。其根本原因在于目前所有的矩阵构造方法都只能在某些特定阶数下有效。例如；Sylvester构造法要求阶数n为2的k次幂；Paley第一构造法要求阶数n满足n为素数幂且n+1是4的倍数；Paley第二构造法则局限于阶数n满足（n/2-1）为素数幂且（n/2-2）是4的倍数等等。因此，为了彻底解决Hadamard矩阵的构造难题，一个仍有待继续努力的研究方向是寻找到一些更为新颖的、巧妙的矩阵设计思路。

3 基于超立方体图的Hadamard矩阵构造法

针对Hadamard矩阵构造问题，本节提出一种新的方法。与之前许多从数论知识出发的构造法不同，本节所提出的构造法则是基于图论的。由于该方法借助了超立方体图的概念，因此，首先介绍超立方体图的定义[15]如下：

定义2 在n维实空间中，取坐标如公式（4）所示的 2n个点{x0，x1，x2，… ，x2n-1}作为顶点集合，对满足公式（5）的顶点对xi和xj之间连一条边，所得到的无向图即为n阶超立方体图。

下图展示了一个四维的超立方体图：

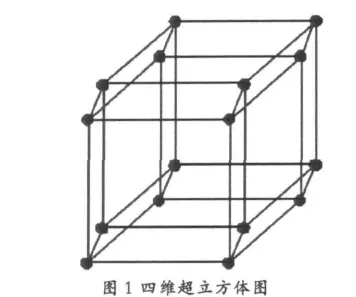
以下详细介绍一种基于图论的n阶Hadamard矩阵构造法。构造法的共分为以下三个步骤：

第一步，构造一个具有n个顶点的超立方体图G。

第二步，对超立方体图G上任意两个点xi和xj，计算它们之间的图上最短路径距离dij。（不失一般性，本文规定超立方体图上的每条边长度均为1。）

第三步，根据第二步的计算结果，按照公式（6）设置矩阵H中的每一个元素的值。

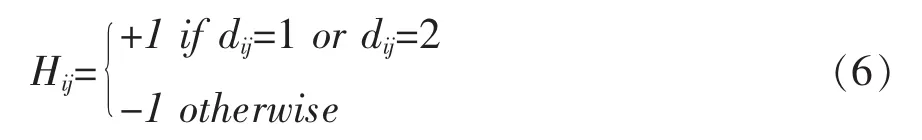
至此，矩阵H即为所要构造的Hadamard矩阵。

4 构造举例

本节以二维超立方体图为例，展示如何构造出四阶Hadamard矩阵。

首先，按照定义2构造出一个二维的超立方体图如下：

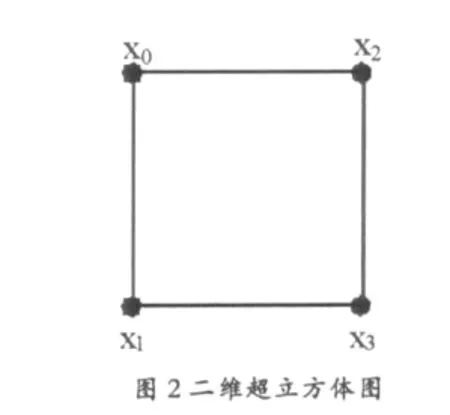
接着，可按照图论方法计算得到如下的最短距离矩阵d：

最后，按照公式（6）最终得到如下的四阶矩阵H：

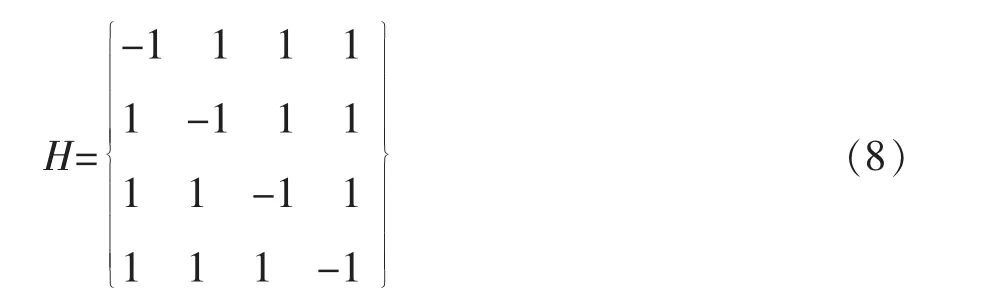
通过计算HHT，不难验证该矩阵确为四阶Hadamard矩阵。

与此类似地，我们可以根据图1构造出十六阶的Hadamard矩阵如下（为了节省篇幅，+1缩写为“+”号，-1 缩写为“-”号）：

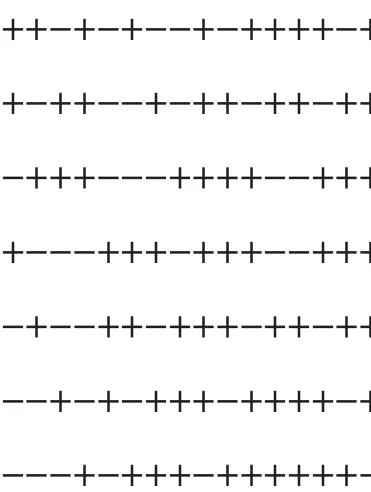
5 结束语

本文针对Hadamard矩阵的构造问题提出了一种新的基于图论的构造方法，并通过实例展示了这种构造方法的可行性。不可避免地，与之前提出的所有构造方法一样，本文所提出构造方法也只能在某些特定阶数下有效。因此，本文的下一步工作是考虑将该方法尝试在阶数上进行推广或者是考虑采用其他图结构来派生出相应的Hadamard矩阵。

[1] J.J.Sylvester.Thoughts on inverse orthogonal matrices,simultaneous sign successions,and tesselated pavements in two or more colours,with applications to Newton's rule,ornamental tile-work,and the theory of numbers[J].Philosophical Magazine,1867,34：461-475.

[2] Douglas R.Stinson.Combinatorial Designs：Constructions and Analysis[M].Berlin：Springer-Verlag,2004.

[3] Bowyer,D.E,Walsh Functions.Hadamard Matrices and Data Compression[J].IEEE Transactions on Electromagnetic Compatibility,1971,EMC-13(3)：33-37.

[4] 乔阳，潘志斌，乔瑞萍，李东平，蔡骋.基于Hadamard变换和矢量分割的快速搜索算法[J].2009,14(11)：2269-2275.

[5] 尹安容,谢湘,匡镜明.Hadamard纠错码结合支持向量机在多分类问题中的应用[J].电子学报,2008,36(1)：122-126.

[6] 夏戈明,黄遵国,王志英.基于对称平衡不完全区组设计的无线传感器网络密钥预分配方案 [J].计算机研究与发展,2008,45(1)：154-164.

[7]Steele,R.Introduction to digital cellular radio.In：Mobile radio communications[M],2nd ed.,IEEE Press,New York,1999.

[8] Michael A.Nielsen.Cluster-state quantum computation[J].Reports on Mathematical Physics,2006,57(1)：147-161.

[9] Michio Ozeki.Hadamard Matrices and Doubly Even Self-Dual Error-Correcting Codes[J].Journal of Combinatorial Theory,Series A,1987,44(2)：274-287.

[10] Marshall Hall.Combinatorial theory[M].2nd Edition.New York：A Wiley InterScience Publication,1998

[11] 沈灏.组合设计理论 (第一版)[M].上海：上海交通大学出版社,1996.

[12] R.E.A.C.Paley.On Orthogonal Matrices[J],Mathematical Physics,1933,(12)：311-320.

[13] JWilliamson.Hadamard's determinant theorem and the sum of four squares[J].Duke Mathematical Journal,1944,11：65-81.

[14]Jennifer Seberry,Mieko Yamada.Hadamard matrices,Sequences,and block designs[M]//Jeffery H.Dinitz and Douglas R.Stinson.Contemporary Design Theory：A Collection of surveys,1992：431-560.

[15] Youcef Saad,Martin H.Schultz.Topological Properties of Hypercubes[J].IEEE TRANSACTIONSON COMPUTERS,1988，37(7)：867-872.