基于椭圆方向窗的非下采样Contourlet域图像去噪算法

金彩虹

(南京晓庄学院物理与电子工程学院，江苏 南京 211171)

图像阈值去噪因其算法简单而成为图像去噪的主流方向，其中，Chen等［1-2］提出的NeighShrink算法，将邻域的概念用于图像去噪，通过计算邻域窗内所有小波系数的平方和来设定阈值，考虑了子带系数的层内相关性，较Donoho［3］的全局阈值能更好地适应图像的细节特征，降低了全局阈值因过度扼杀分解系数造成的图像细节的损失。但是，NeighShrink算法采用各向同性的正方形邻域窗对系数进行阈值处理，没有考虑子带能量聚集的方向特性，在信号的能量聚集处不能获得最优的去噪效果。另外，由于二维小波基函数的支撑区间是正方形，当尺度变细时，二维小波只能用点来逼近图像中具有线奇异特征的边缘细节，不能实现对图像的最优稀疏逼近。2006年，Cunha等［4］提出非下采样Contourlet变换的概念。该变换基函数支撑区间不是正方形，而是长度的平方与宽度成正比，当尺度变细时，Contourlet基函数用类似于线段的长条形结构来逼近图像，实现了图像的最优稀疏逼近。而且，该变换没有下采样过程，变换具有平移不变性，能有效抑制小波变换由于不具有平移不变性特征而造成的恢复图像的伪吉布斯失真。

本文根据图像经多尺度多方向非下采样Contourlet分解后，各方向子带不同的能量聚集特性，用主轴方向与子带频率分解方向正交(也就是图像能量聚集方向)、长轴与短轴的比例与非下采样Contourlet基函数支撑区间相匹配的椭圆方向窗作为邻域窗，通过最小化Stein的无偏风险估计，确定该邻域窗的最佳大小和最佳阈值。然后在该最佳椭圆方向窗内，用最佳阈值对窗中心系数进行基于NeighShrink算法的阈值去噪处理，实现信号与噪声的有效分离。

1 非下采样Contourlet变换

Cunha等［4］提出由非下采样塔状滤波器组(nonsubsampled pyramid，NSP)将图像分解为低频部分和高频部分，再由非下采样方向滤波器组(nonsubsampled directional filter banks，NSDFB)将高频部分分解为若干个方向，实现对图像的非下采样Contourlet变换。非下采样塔状滤波器组(图1)采用àtrous算法［5］设计满足Bezout恒等式［6］的双通道滤波器结构。能实现完全重构的滤波器组满足:

式中:H0(z)——低通分解滤波器;H1(z)——高通分解滤波器;G0(z)——低通重构滤波器;G1(z)——高通重构滤波器。

图1 非下采样塔状滤波器组Fig.1 Non-subsampled pyramid filters

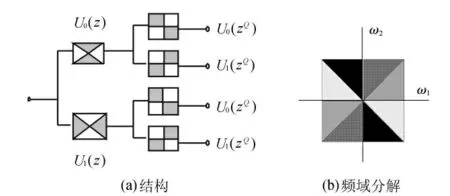
图2 非下采样方向滤波器组Fig.2 Non-subsampled directional filter banks

大小为N×N的图像f(x，y)经非下采样Contourlet变换，可表示为

式中:bJ——低频子带系数;cj，k(m，n)——高频子带系数;j——系数所在尺度;k——系数所在方向;2lj——j层总的分解方向数;m，n——系数所在位置。

2 基于椭圆方向窗的邻域图像去噪算法

设二维含噪图像Y(x，y)=f(x，y)+N(x，y)，f(x，y)是期望图像，N(x，y)是方差为的高斯白噪声。NeighShrink图像去噪算法，根据邻域窗rx，y内所有高频子带系数平方和的大小决定窗中心系数cj，k(m，n)是置零还是收缩，即邻域窗中心系数cj，k(m，n)的估计值(m，n)为

式中λ为阈值。

cj，k(m，n)估计的准确度由阈值和邻域窗的大小及形状决定。传统阈值采用universal全局阈值，邻域窗选择固定大小的方形窗［8-10］(如3×3，5×5等)或有一定自适应能力的方形窗［11-12］。然而，图像经多级非下采样Contourlet分解后，各方向子带能量分布与分解尺度成反比，且方向子带能量呈现出各向异性的聚类特性。而高斯噪声的能量是近似均匀地分布在各子带上的，所以，采用universal全局阈值和固定大小的方形窗来估计高频子带系数cj，k(m，n)会引入过多的噪声，降低信号水平。为保护图像的边缘方向信息，采用主轴方向与图像能量聚集方向一致，长、短轴之比与非下采样Contourlet基函数支撑区间相匹配的椭圆方向窗，并通过最小化Stein的无偏风险估计确定椭圆方向窗的最佳大小和该窗内的最佳阈值，在此椭圆方向窗内估计高频子带系数cj，k(m，n)将能获得比在正方形方向窗内更优的性能。

j尺度k方向子带上的椭圆方向窗［13］W(r，a，φj，k)定义为

椭圆方向窗的形状，即椭圆长、短轴之比a2为

式中C为常数，C的大小会改变椭圆方向窗的面积，但不影响椭圆方向窗的长、短轴之比。由式(6)可见，第j层的分解方向数2lj越多，基函数支撑区间长、宽比越大，椭圆方向窗相应越狭长。

椭圆方向窗的主轴方向φj，k为

由式(7)可见，第j层上不同方向子带的椭圆方向窗的主轴方向与子带频率分解方向正交。

椭圆方向窗的大小r通过最小化Stein的无偏风险估计来确定。在均方误差(MSE)准则下，根据j尺度、k方向子带上r邻域窗内有噪图像系数cr(为方便表达式的书写，省略了系数的尺度、方向和位置的标注)确定无噪图像的估计值^θr，就是使无噪图像的真实值θr与^θr的均方误差最小。θr与^θr的均方误差为

式中Nr为j尺度、k方向子带上r邻域内系数个数。由于无噪图像的θr不可能得到，所以，在大小为r、阈值为λ的邻域窗内，采用Stein无偏风险估计，则均方误差变为

根据(3)式有

最优阈值λt和最佳大小的椭圆方向窗rt，就是使SURE(cr，λ，r)最小，即

非下采样Contourlet域内，基于椭圆方向窗的邻域图像去噪算法步骤为:(a)对含噪图像进行多尺度、多方向非下采样Contourlet变换，得到bJ和各尺度不同方向的cj，k(m，n)。(b)对最高尺度bJ给予完全保留，不作任何处理。bJ反映的是整个图像的概要，几乎不包含高频成分，当然也就没有噪声信息。(c)对j尺度、k方向的cj，k(m，n)按式(3)进行邻域收缩。式(3)中的阈值和子带大小用式(16)的计算结果，邻域窗的形状由式(6)给出，邻域窗的主轴方向由式(7)给出。(d)将收缩处理后的cj，k(m，n)和没有处理的bJ一起进行非下采样Contourlet逆变换，得到去噪后的恢复图像。

3 试验结果与分析

为验证本文算法的有效性，在MATLAB7.0中选择叠加均值为零，标准差σ分别为15，20，25，30的白噪声的Lena和Barbara标准测试图像进行试验。试验对文献［1］中的NeighShrink算法、文献［11］中的邻域小波系数自适应降噪算法、文献［12］中的先优化后分类改进的小波域去噪算法和本文算法进行了比较。试验中前3个算法中的小波变换选择db8小波，图像进行4层小波分解，本文算法中的非下采样Contourlet变换选择“9-7”塔式分解和方向滤波器组，图像进行4层分解，各层方向数为4，4，8，16，各层椭圆方向窗长、短轴之比a2分别为1，1，2，4。NeighShrink算法采用Chen等［1-2］推荐的universal全局阈值和3×3的固定邻域窗，其他两种算法采用原作者建议的自适应窗和阈值。去噪结果的客观评价指标用峰值信噪比(PSNR)衡量。表1比较了不同噪声等级下各种算法的PSNR，图3为噪声标准差为20时各种算法对Barbara含噪图像的去噪结果。

由表1可见，采用本文算法得到的恢复图像的PSNR值比采用文献［1］算法得到的恢复图像的PSNR值高2.70～3.15 dB，比采用文献［11］算法得到的恢复图像的PSNR值高2.54～2.96 dB，比采用文献［12］算法得到的恢复图像的PSNR值高2.33～2.62dB。采用本文算法得到的恢复图像的PSNR值高于采用其他3种算法得到的恢复图像的PSNR值，尤其优于文献［1］算法。

表1 几种算法的去噪图像峰值信噪比Table 1 Comparison of PSNRs(dB)of de-noised images obtained with different algorithms

图3 噪声标准差σ=20的Barbara测试图像的去噪结果比较Fig.3 De-noising results of different algorithms for Barbara pictures at noise levelσ=20

从图3的视觉效果图中可以看出，文献［1］算法由于去噪时采用的universal全局阈值和3×3的固定方形邻域窗，导致去噪后的恢复图像有比较明显的方块效应。文献［11］和［12］中采用了自适应窗和阈值，恢复图像的视觉效果明显好于采用文献［1］算法得到的恢复图像，没有明显的方块效应，但图像的纹理细节在去噪的同时有所模糊。本文利用子带能量的聚类各异性，采用长、短轴之比与该尺度下非下采样Contourlet基函数的支撑区间相匹配，邻域窗的主轴方向与图像能量聚集方向一致的椭圆方向窗，并通过最小化Stein的无偏风险估计获得椭圆方向窗的最佳大小和该窗内的最佳阈值后对窗中心的系数估计，去噪后的恢复图像较其他3种算法保留了更多的细节信息，图像中大多数纹理特征的结构都能被清晰地还原出来，甚至是Barabara围巾边缘上的细小纹理也得到了较好的恢复。

4 结 语

非下采样Contourlet变换用类似于线段的基结构来逼近图像，图像经多尺度、多方向非下采样Contourlet分解后，能量主要聚集在低频子带，高频子带上图像的能量很少，而且子带频率越高其上的能量越少，各方向子带信号能量是沿着与子带频率分解方向正交的方向聚集的。基于子带能量的这种聚类特性，采用本文定义的椭圆形方向窗对窗内的系数进行去噪处理，可以去掉正方形方向窗中不在能量聚集方向上的点，保证剩下点的方差更接近于待估计点的方差，实现了在能量聚集处对高频子带系数的最佳估计。试验结果表明，该算法克服了恢复图像中的伪吉布斯失真，在去除噪声的同时尽可能多地保留了图像的边缘和纹理细节，提高了去噪后恢复图像的信噪比，获得了视觉效果良好的恢复图像。

［1］CHEN G Y，BUI T D，KRZYZAK A.Image denoising using neighbouring wavelet coefficients［J］.Integrated Computer-Aided Engineering，2005，12(1):99-107.

［2］CHEN G Y，BUI T D，KRZYZAK A.Image denoising with neighbour dependency and customized wavelet and threshold［J］.Pattern Recognition，2005，38(1):115-124.

［3］DONOHO D L.De-noising by soft-thresholding［J］.IEEE Trans on Information Theory，1995，41(3):613-627.

［4］CUNHA A L，ZHOU Jianping，DO M N.The nonsubsampled contourlet transform:theory，design，and applications［J］.IEEE Trans on Image Processing，2006，15(10):3089-3101.

［5］SHENSA M J.The discrete wavelet transform:wedding theàtrous and mallat algorithms［J］.IEEE Trans on Signal Processing，1992，40(10):2464-2482.

［6］杨福生.小波变换的工程分析与应用［M］.北京:科学出版社，2001:77-85.

［7］金彩虹.基于非下采样Contourlet变换的图像自适应阈值去噪算法［J］.华中师范大学学报，2011，45(1):37-42.(JIN Caihong.Adaptive thresholding for image denoising via nonsubsampled contourlet transform［J］.Journal of Huazhong Normal University，2011，45(1):37-42.(in Chinese))

［8］SHYAM A C，JYOTINDER S.Wavelet domain non-linear filtering for MRI denoising［J］.Magnetic Resonance Imaging，2010，28(6):842-861.

［9］CAO X，SHEN W.Illumination invariant extraction for face recognition using neighboring wavelet coefficients［J］.Pattern Recognition，2012，45(4):1299-1305.

［10］李恒超，洪文，吴一戎.基于尺度空间相关的SAR图像NeighShrink滤波算法［J］.电子与信息学报，2008，30(8):1940-1943.(LI Hengchao，HONG Wen，WU Yirong.NeighShrink despeckling for SAR images based on scale space correlation［J］.Journal of Electronics＆Information Technology，2008，30(8):1940-1943.(in Chinese))

［11］周登文，申晓留.邻域小波系数自适应的图像降噪［J］.中国图形图像学报，2008，13(11):2112-2116.(ZHOU Dengwen，SHEN Xiaoliu.Adaptive image denoising using neighbouring wavelet coefficients［J］.Journal of Image and Graphics，2008，13(11):2112-2116.(in Chinese))

［12］李柯材，张曦煌.先优化后分类改进的小波域图像去噪方法［J］.计算机工程与应用，2011，47(8):186-189.(LI Kecai，ZHANG Xihuang.Improved image denoising method of first optimization and last classification in wavelet domain［J］.Computer Engineering and Applications，2011，47(8):186-189.(in Chinese))

［13］SHUI P L.Image denoising algorithm via doubly local wiener filtering with directional windows in wavelet domain［J］.IEEE Signal Processing Letters，2005，12(10):681-684.