一种改进的小波阈值裂纹图像去噪法

夏 欣，李海标，沈兰兰，秦泽熙

（桂林电子科技大学 广西 桂林 541004）

随着大规模、超大规模集成芯片的制造，芯片的裂纹已逐渐成为最大的隐患。然而芯片表面的边缘错综复杂，因此，迫切需要一个更有效的方式来获得更清晰的边缘图像，进行表面的裂纹检测。图像噪声严重影响了图像质量，对图像处理非常不利，需要进行图像去噪。直接对图像空间域进行分析是非常困难，但是通过将空间域转换成频率域后，就可以很好地克服空间域难处理的弱点，并得到一个更方便的解决问题的办法。一般可以通过傅立叶变换，将时间信号转换成频率信号，并确定了信号在整个时间域上的频率特性。但事实上，需要知道信号在某一时刻附近的频谱特性，傅立叶变换是无法做到的[1-2]。

基于以上原因，有必要使用一种前沿图像处理理论进行图像分析，这种理论就是小波阈值去噪理论。它是将空间图像通过小波变换到频域图像后进行处理，从而将噪声和图像原始信息分离，以获得一种更接近理想图像去噪理论。小波变换是因为傅立叶变换发展的局限性而诞生，二者有着很多本质上的相同之处。从20世纪后半页，1981年小波变换由法国地质物理学家J.Morlet提出，从而拉开了小波变换迅猛发展的序幕[3]。这种空间-频率分析的方法得到了全世界的认可，这也带动了小波变换的迅猛发展。小波变换具有多分辨率的特点，使得小波分析能从含有噪声的图像中提取原始信息，从而达到去噪的效果。小波变换中，最常用的去噪方法就是小波阈值去噪法。小波阈值去噪理论是图像去噪的一个非常重要的应用领域。小波变换成功地应用在许多科学领域，例如图像压缩、图像去噪、信号处理、电脑绘图、模式识别。

1 理论基础

随着数字图像处理的迅猛发展，诞生了许多图像去噪方法。传统的图像去噪方法大致分两大类：一类是空间域方法。这种方法主要利用图像平滑模板对图像进行卷积处理，以抑制或消除噪声为目的。常用方法包括：线性滤波法、中值滤波法等。线性滤波法中最典型的是均值滤波器。1991年Coyle采用这种方法，可以很好地滤除高斯噪声。由于线性滤波法无法处理非线性问题，因此，1971年Turky提出了中值滤波法，中值滤波法是一种典型的非线性滤波[4]。这种方法可以快速和有效地滤除噪声，但它不能理想地保护图像的边缘，导致图像的细节变得模糊，因此，出现了许多基于中值滤波器的改进方法；另一类是频率域方法，主要是将空间域图像变换成频率域图像，然后选用适当的频率带通滤波器进行滤波处理。常用的有如下几种方法：傅里叶变换和小波变换等。小波变换是将含有噪声的采样值在某一尺度下分解到不同的频带内，然后再将噪声所处的频带置零，再利用相应的重构公式进行小波重构，从而达到去除噪声的目的。

相对于传统去噪方法，小波变换具有多分辨率的特点，在时域和频域都有表征信号局部信息的能力，能有效地从正常信号中提取瞬态成分，可以应用于图像去噪。小波去噪方法大体分成小波阈值法、投影方法和相关方法。小波阈值法是目前研究最为广泛的方法。阈值化方法的基本依据是同一区域内，各像素的灰度特性具有一致性。该方法的基本思想是利用图像的特性，得到一个灰度阈值，然后将图像中所有像素的灰度与这个阈值相比较，将像素灰度大于这个阈值的所有像素组合成一类，而像素灰度小于这个阈值的所有像素组合成另一类。通过调整阈值大小，从而更好地实现图像原始信息与图像扰乱信息的分离[5]。

小波阈值去噪的理论基础：在小波域中，图像能量集中在有限数量的小波系数，而噪声分布在整合小波域中。因此，在小波分解中，图像的小波变换系数大于噪声的小波变换系数，从而获得一个分离图像和噪声的方法。假设图像中混有高斯白噪声，可以把正副图像表示成：

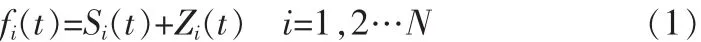
在这个方程中，Si（t）表示图像的原始信息，Zi（t）表示标准高斯白噪声。如果想从含有噪声图像中提取原始图像Si（t），需要以下几步执行：

1）选择适当的小波分解 fi（t）图像及小波分解深度 j，得到相应的小波分解系数。

2）处理小波分解系数得到阈值系数 ωj，k，估计原始图像的阈值系数。

3）对阈值处理后的系数通过小波逆变换重建原始图像。

2 改进小波阈值图像去噪法

为了获得高品质的图像，需要对小波阈值进行评估，常用的小波阈值是由Donoho等提出的通用阈值公式：

其中，σ是噪声的标准方差，n是信号的采样长度。然而，直接估计的小波阈值的阈值公式会出现“过扼杀”现象，导致图像边缘细节出现丢失现象。为了保护图像的边缘细节，需要阈值公式进行优化。文中采用引入收缩因子的方法，通过改变阈值大小，从而更多地保留图像边缘信息。如果引入收缩因子的值过小，会导致获得的阈值太小，施加阈值后的小波系数中将包含过多的噪声分量，达不到有效去噪的目的。相反，如果引入一个收缩因子的值过大，图像的原始信息就会丢失得更多，导致图像模糊。为了保证图像边缘完整和消除噪声的效果，因此，需要引入一个适中的收缩因子，可以自适应地选择最佳的小波变换的分解层数，以达到去噪及边缘保护的要求。其数学表达式为：

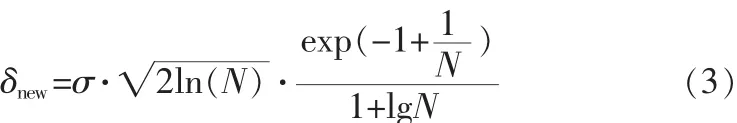
其中δnew表示新的阈值公式，N表示总层数。

小波阈值去噪过程中需要对小波系数进行阈值处理，目前两种常用的阈值方法是硬阈值法和软阈值法。由Donoho提出的小波硬阈值法和小波软阈值法进行小波系数的估计[6]。其定义分别为：

1）硬阈值函数定义为:

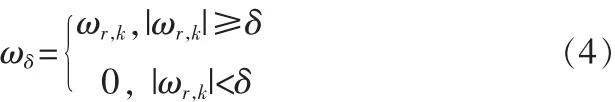
其中ωr，k是小波系数，δ是阈值。把绝对值小于阈值δ的系数置0，并且使保留下来的小波系数与原始系数更接近。

2）软阈值函数定义为:

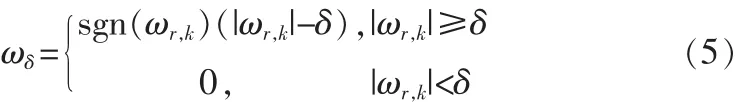
将绝对值小于阈值δ的小波系数置0，sgn（·）是符号函数，而对大于阈值δ的小波系数用δ来进行缩减处理。

虽然硬阈值是自然的选择，能够很好地保留图像边缘细节，但由于硬阈值函数不连续，会引起去噪图像中出现振铃、伪吉布斯效应；虽然软阈值处理相对平滑，会减少振铃、伪吉布斯效应，但由于存在固有的偏差，会造成图像模糊。针对硬阈值函数和软阈值函数的缺陷，提出了对软阈值与硬阈值折中的处理方法，给出了半阈值函数为：

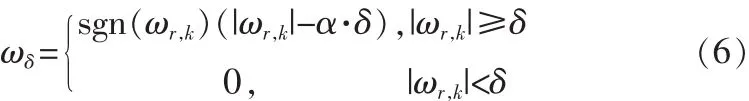
其中，α的取值范围是0～1，该方法估计出来的小波系数ωδ介于软、硬阈值方法之间，能够改善振铃、伪吉布斯效应等视觉失真和边缘模糊现象，但是由于参数在实际操作中的经常取值为某一常数，不具有自适应性，因此仍然会存在固有偏差和不连续。

针对硬阈值函数、软阈值函数以及半阈值函数存在的缺陷，为了寻找更好的阈值函数，发现比较合理的阈值函数需满足一下几点：

1）表示信号的小波系数基本保持不变，较好地保留图像边缘细节。

2）较小的振铃、伪吉布斯效应。

3）阈值函数具有自适应性。

自适应是通过|ωr，k|与阈值δ比较实现的。为此笔者提出具有自适应特点的新阈值函数：

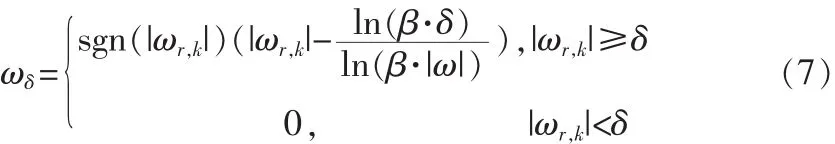
基于改进阈值的小波图像去噪的具体步骤如下：

1）小波分解：对图像进行N层离散小波分解；

2）阈值处理：采用阈值修正方案确定阈值大小，用新阈值函数对小波系数进行处理；

3）图像重构：通过小波逆变换重建图像。

3 实验结果与分析

利用Matlab7.0进行仿真，实验中图像去噪算法所采用的小波函数与分解层数都相同，小波函数为Daubechies系列的db5，分解层数N取值为5。α取值0.5，新阈值函数中的β取一个适中的值5。

采用通用阈值方案、硬阈值函数进行去噪的方法称为硬阈值函数去噪法；采用通用阈值方案、软阈值函数进行去噪的方法称为软阈值函数去噪法；采用通用阈值方案、新阈值函数进行去噪的方法称为新阈值函数去噪法。

图1是通过CCD获取的原始图像，图像完整清晰。图2是加入高斯噪声的含噪声图像，图像整体出现斑点且模糊；图3是硬阈值函数去噪法去噪结果图像；图4是软阈值函数去噪法去噪结果图像；图5改进阈值去噪法去噪结果图像。图3与图4由于是采用通用阈值方案确定阈值，在去噪过程中边缘轮廓部分丢失，较小孤立细节图像丢失严重；而图5是采用阈值修正方案进行阈值估计，减少了图像边缘轮廓和图像弱细节的丢失.说明阈值修正方案有利于保护图像边缘细节。图3是采用硬阈值函数进行阈值处理，图像较为清晰，但出现了较严重的振铃和伪吉布斯效应；图4是采用软阈值函数进行阈值处理，出现图像模糊，部分边缘轮廓甚至无法辨认；图5是说明新阈值函数改善了图像的视觉效果，去噪后图像更接近原始图像。

图1 原始图像Fig.1 Original image

图2 含高斯噪声图像Fig.2 Noisy image

图3 硬阈值去噪Fig.3 Hard-TF denoising

图4 软阈值去噪Fig.4 Soft-TF denoising

图5 新的阈值方法Fig.5 Improved method

4 结 论

文中提出了一种改进的小波阈值方法，保证图像处理时获得一个清晰的图像，为后续的目标跟踪、检测和识别提供一个可靠的依据。阈值去噪方法的两个基本要素阈值和阈值函数都得到了改进。第一步，引入的收缩因子能有效地优化阈值自适应能力；第二步，该改进的小波阈值方法相比其他阈值函数能更有效去除数字图像噪声；第三步，采用仿真实验进行实验对比。结果表明，改进的小波阈值方法可以有效地去除数字图像噪声、达到更好的边缘保持指数、视觉效果和更高的峰值信噪比。然而，去噪图像仍然存在一些缺陷。因此，需要作进一步的优化小波阈值去噪法。

[1]胡家顺，冯新，李昕，等.裂纹梁振动分析和裂纹识别方法研究进展[J].振动与冲击，2007，26（11）:146-150.

HU Jia-shun，FENG Xin，LI Xin，et al.State-of-art of vibration analysis and crack identification of cracked beams[J].Journal of Vibration and Shock，2007，26（11）:146-150.

[2]范永法，郑长宏，等.用于表面裂纹自动检测的图像识别算法[J].机械设计与制造，2002（4）:80-82.

FAN Yong-fa，ZHENG Chang-hong，et al.Image identification algorithm used in automatic inspection of surface cracks[J].Machinery Design&Manufacture，2002（4）:80-82

[3]韦力强.基于小波变换的信号去噪研究[D].长沙:湖南大学，2007.

[4]Coyle E J，Gabbouj M，Lin J H.From median filters to optimalstackfiltering[J].IEEEInternat.Symp.CircuitsSystems，1991（1）:9-12.

[5]崔华，宋国乡.基于小波阈值去噪方法的一种改进方案[J].现代电子技术，2005（1）:8-10.

CUI Hua，SONG Guo-xiang.A kind of modified project based on the wavelet treshold denoising method[J].Modern Electronic Technique，2005（1）:8-10.

[6]Donoho D L.De-noising by soft-thresholding [J].IEEE Transactions on Information Theory，1995，41（3）:613-627.