低功耗低温漂高PSR带隙基准电压源的设计

万志荔，赖史胜，章珍珍，马连川

（1.赣南医学院第一附属医院 江西 赣州 341000；2.北京交通大学 电子信息工程学院，北京 100044）

生物医学信号属于强噪声背景下的低频微弱信号，它是由复杂的生命体发出的不稳定的自然信号。

若是要处理和分析非常微弱的生物医学信号，需要先对该信号放大、采样，进而进行相应的数字处理。而放大器、AD（Analog-Digital）转换电路都需要精准的基准电压源。

同样在模拟电路中，电压源是至关重要的单元。而带隙基准电压源因为其独特的优点，如结构简单、低压、低功耗、低噪声、高PSR、适用于 CMOS工艺等，得到了广泛的应用。因此，获得高精度、低功耗、低噪声、低成本的带隙基准源以满足微弱医学信号放大的目的，将是模拟电路设计者不断努力的方向。

基于该目的，本文设计实现了一种适用于微弱医学信号放大电路的带隙基准电压源：采用一种新型的高阶温度补偿方式，获得极低温度系数（TC）；同时提出一种预稳压技术，提高了带隙基准电压源的电源抑制比（PSR）。

1 带隙基准电压源的工作原理

带隙基准电压源可以简化为如图1所示的基本框图。在图1中，寄生pnp双极性晶体管的基极-射极两端电压VBE是负温度系数电压，为了补偿Vbe使输出电压VREF为零温度系数，就必须加入正温度系数（PTAT）电压。而热电压VT=kT/q（k为波尔兹曼常数，T为绝对温度，q为电子电荷量）就是这样一种PTAT电压。且在CMOS工艺中kT/q可以由工作在不同集电极电流密度的寄生pnp管产生。这样，通过调节VT的放大系数Kp，可以使VREF=Vbe+Kp×VT获得零温度系数。

首先，考虑负温度系数电压VBE。

1980年Tsividis在文献[1]中对VBE的温度模型进行了详细推导，得到了如式（1）的VBE关于温度T的精确模型。

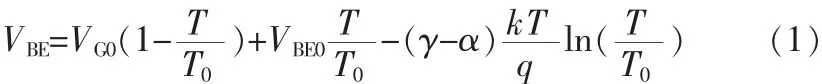
其中，VG0为绝对零度下基极-射极电压，VBE0为参考温度T0下的基极-射极电压，γ为迁移率的温度因子，且有γ≈4，α为集电极电流的温度因子。由（1）式可知，VBE随温度变化呈非线性关系。且因为VG0＞VBE0，其一阶斜率为负数，这使得VBE为负温度系数电压。

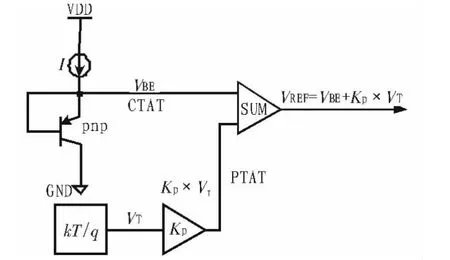
图1 带隙基准电路的基本原理Fig.1 Basic structure of bandgap reference

图2 正温度系数电压产生电路Fig.2 Generation of PTAT voltage

接着，考虑PTAT电压。

根据式（1），对于2个工作在不相等的电流密度下（电流密度之比为N）且面积比为M的双极晶体管，如图2，如果它们的工艺参数都一样，那么可以得到它们的基极－发射极电压的差值ΔVBE的表达式为：

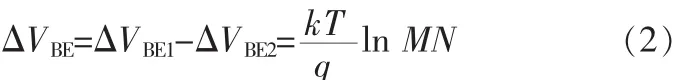
在式（2）中，ΔVBE随绝对温度T线性变化，且斜率为正。因此，ΔVBE可以作为PTAT电压。

通常，一阶温度补偿方式就是简单地叠加VBE、ΔVBE，使它们的正负一阶温度斜率相抵消。但是经过一阶补偿后的带隙基准电压最好也只能获得20 ppm/℃的温度系数。

造成这种现象的原因是式（1）中VBE存在非线性温度项TlnT，它限制了VREF的温度系数。而怎样补偿该非线性温度项也就成为设计带隙基准电路的关键。

为了补偿非线性温度项TlnT，许多论文提出了带隙基准电压源的高阶温度补偿技术：1）利用2个偏置在具有不同温度系数的集电极电流的双极型晶体管的ΔVBE具有温度高阶项的高阶补偿技术[2]。2）利用ΔVGS的温度高阶项的高阶补偿技术[3]。3）利用与温度成非线性关系的电阻的高阶补偿技术[4]。4）利用双极型晶体管的电流增益因子β与温度成指数关系的特性的指数补偿技术[5]。5）利用具有温度系数的电阻的串并联得到温度高阶项的高阶补偿技术[6]。

2 新型高阶温度补偿方式

与传统补偿方式不同，本文在文献[7]的基础做出改进，并提出了一种新型的高阶温度补偿方式，如图3所示。其基本原理有两点：将PTAT电流和TlnT项电流流经电阻以产生一阶温度电压和TlnT电压，补偿低温范围内VBE；利用pn结反向电流随温度升高而增大特性补偿高温范围内的温度系数。

图3 本文提出的带隙基准电压源核电路Fig.3 Core circuit of proposed bandgap reference

2.1 低温范围内温度补偿方式

在图3中，各支路电流都为IP。首先根据式（1），得到Q1、Q2、Q3、Q4的基极－射极电压为：

式中 x 对应 1、2、3、4，且有 α1=α2=α4。

由于运算放大器OP1工作在深度负反馈状态，钳制A点电压等于B点电压，使得流经电阻R2的电流为：

将式（3）代入式（4）得：

式中，k1为Q3与Q1面积之比，k2为 Q4与Q2面积之比。

再将 IP流入R1后和VBE叠加构成VREF：

将上述表达式简化为：

其中：

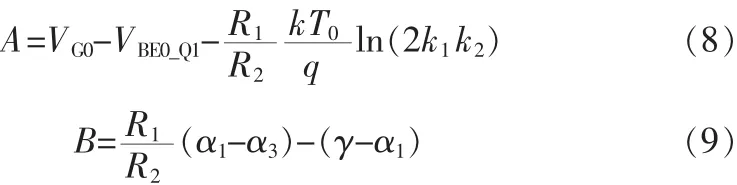
为了使VREF与温度无关，A，B必须都为0。在式（8）中，在工艺、k1k2都确定的情况下，由A=0可得到R1与R2的比值为：

在实际设计中，可以调节R1/R2的大小，来满足式（10）。

同理，在式（9）中，由于 R1/R2已经由式（10）确定，根据B=0可以确定α3的值：

由于α为集电极电流的温度因子，即有：

其中IP0为T0温度下集电极电流。

而式（5）显示在低温情况下，近似有 Ip∝T，即 α1≈1。 而γ≈4，则满足（γ－α1）R2/R1＞0，因此有 α3＜α1。 这就意味着流入Q3的电流I3并不只是IP，还必须加入负温度系数的电流IC。

为了得到电流IC，在图3中，运算放大器OP2钳制C、D点电压相同，使得流经R3的电流为：

由于VBE_Q1为CTAT（互补温度系数）电压，其温度系数为负，IC也为CTAT电流。该电流经过电流镜偏至Q3射极中，即I3=IC+IP，这样就可以得到温度系数小于α1的电流。同时由于α3与α1呈一一对应关系，IC也与IP一一对应。

在实际设计中，在R2已经确定的情况下，为了满足式（11），可以改变流入Q3射极的负温度系数电流IC大小，也即调节R3/R2的大小，来获得合适的α3。

综上所述，通过调节R1/R2，R3/R2的值，就可以在低温范围内获得零温度系数的基准电压。

2.2 高温范围内温度补偿方式

由于IP并是温度的高阶多次函数，这使得α1随着温度改变而改变。这也就意味着式（11）只是在一定温度范围内近似成立。因此，上述温度补偿方式并不完美。

为了更好的理解这个问题，我们再回到式（5）：由于α1＞α3，kT/q×ln（T/T0）的系数为正，这使得温度越高，T 的更高次项所占的比重越大，IP的温度因子α1也越大。同时，VBE_Q1的温度系数随温度升高而减小，这使得α3的增量小于α1的增量，即 α1－α3也随温度升高而增大。 在 R1、R2、R3都不变的情况下，由式（9）可知，随着温度升高，B随之增大，最终使VREF也跟着增大。

因此，可以得出结论：上述温度补偿方式不适合高温范围的温度系数补偿。

为了进一步对VREF进行高阶温度补偿，本文利用pn结反向电流随温度增大而增大的特性，在输出端连接一个由nmos构成的反向pn结。如图3所示，晶体管的栅源漏极都连接在输出端上，衬底接地。随着温度升高，pn结反向电流增大，晶体管从IP中的分流也越大，使得电阻R1两端的压降减小，最终补偿了VREF使其不随温度变化。

需要指出的是，由nmos管构成的反向pn结只在高温范围内（T＞100℃）才有显著的电流，它在低温范围内对VREF没有影响，不会干扰低温温度补偿，其反向漏电特性如图4所示。

3 预稳压技术提升PSR

带隙基准电压源的另一个重要指标就是电源抑制（PSR）特性，它反映了输出电压随电源电压变化的程度，PSR越高，输出基准电压受电源电压波动的影响越小，反之，则越大。

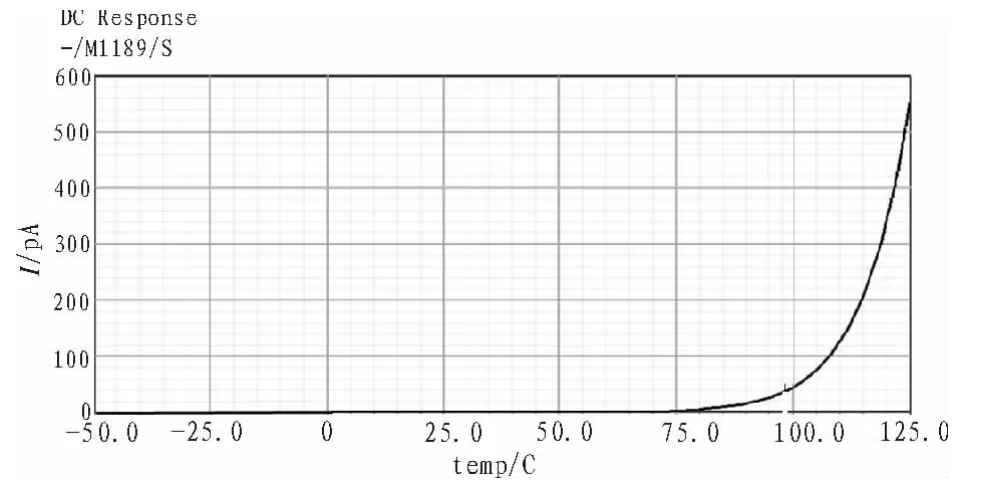
图4 NMOS 管反向漏电（W=5u，L=5u）Fig.4 Reverse leakage current of NMOS（W=5u，L=5u）

为了提高电路的PSR，本文首先在核电路的基础上采用了cascode共源共栅结构，使电路的低频PSR提高到了－80 dB左右。 同时，还引入了预稳压器（Pre－Regulator）[8]，通过预稳压技术使低频PSR从－80 dB提高到了－127 dB。

如图5，预稳压器的原理是通过负反馈，产生一个与电源电压无关的电压VREG，给带隙核电路供电。具体过程是：当VREG有一个小信号变化vreg时，由于M1栅极电压VA连接的是运放OP1的输入端，运放的负反馈作用使它的电压基本不变，在理想情况下保持在VA=VBE_Q1+VBE_Q2，这样M1的漏极电流增大 gm1vreg，M5的栅极电压也增大 gm1vregr3（r3为 M1、M2、M3、M4构成共源共栅结构在M3漏端的输出电阻），最终通过M5的共源极负反馈作用使VREG减小gm1vregr3gm5rreg（rreg为在VREG端看到的总电阻）。因此，Pre－Regulator可以看成一个具有高环路增益的负反馈环，其环路增益为：

其中β为运算放大器OP1的非线性因子，它与放大器的增益、带宽、电源抑制比等特性有关，对于理想运算放大器，β=1。

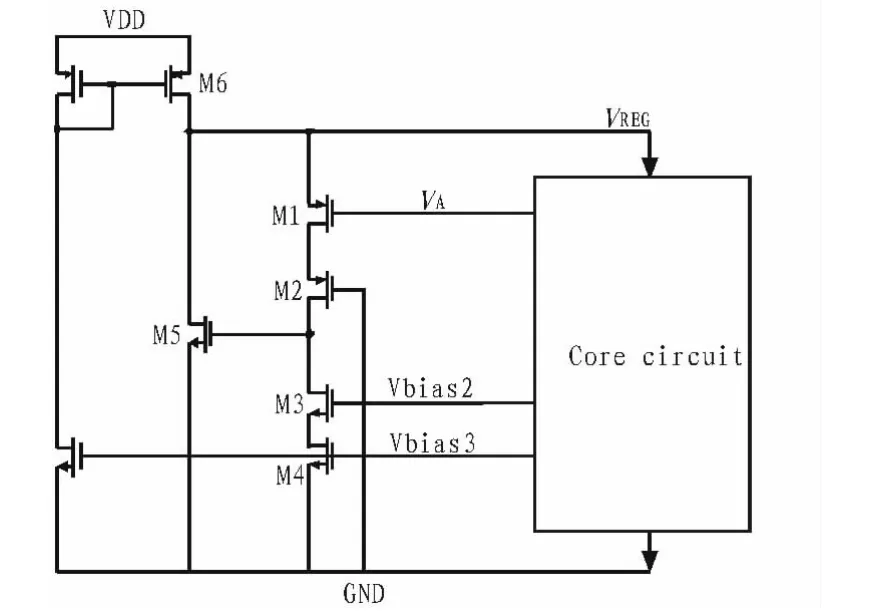
图5 Pre－Regulator原理图Fig.5 Pre－Regulator schematic

我们定义VREG到VDD的电源抑制为：

由式（14）可知，VREG到VDD的电源抑制为：

上式中假设β=1。

为了计算整个电路的低频PSR，我们将带隙核电路和预稳压电路结合得到整个带隙电路，如图6。首先计算VREF到VREG的电源抑制PSRcore：假设VREG有一个小信号增量vreg，然后计算输出端的小信号增量vref。画出输出端VREF的小信号模型如图7。

图6 本文提出的带隙基准电路Fig.6 Proposed bandgap reference circuit

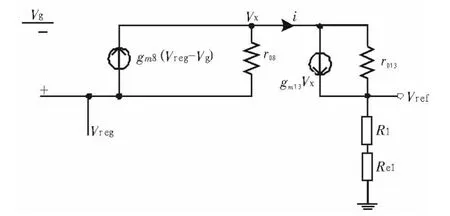
图7 输出端小信号模型Fig.7 Small signal model of output port

在图7中，vg为OP1输出端电压，且有vg=iA1（R2+Re4-Re2）。由上述小信号模型可解得PSRcore为：

其中，Re1、Re2、Re4分别为 Q1、Q2、Q4射极到地的电阻。

而整个电路的PSR可以看做是VREG到VDD的电源抑制与VREF到VREG的电源抑制之和，即：

4 Spectre仿真结果

本电路基于 tsmc0.35 μm CMOS工艺设计实现，在Cadence环境下采用spectre对所设计电路进行仿真验证。图8-图11描绘的是各个corner下，VREF随直流电源电压、温度、工艺变化以及PSR的仿真曲线。从图中可以看出，该带隙基准电路工作电压可以低至2 V；电路的PSR在10 Hz时最好可达-127.5 dB（tt），最差也能达到-110 dB（ss），而 100 kHz时，PSR仍可以达到-63 dB；不同工艺、温度下，输出电压VREF最大变化量小于110 μV，而同一温度，不同corner下VREF的差值最大也仅为61.5 μV；温度在-40~125℃范围内变化时， 输出电压 VREF的温度系数在 0.445 ppm/℃（sf）~0.604 ppm/℃（ss）之间。详细仿真参数如表1所示。

表1 本文提出的带隙基准电路仿真结果Tab.1 Simulation results of theproposed bangap referencecircuit

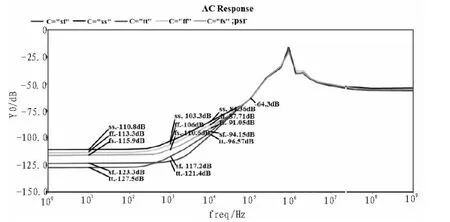
图9 不同corner下，PSR随频率变化曲线Fig.9 PSR at different corners

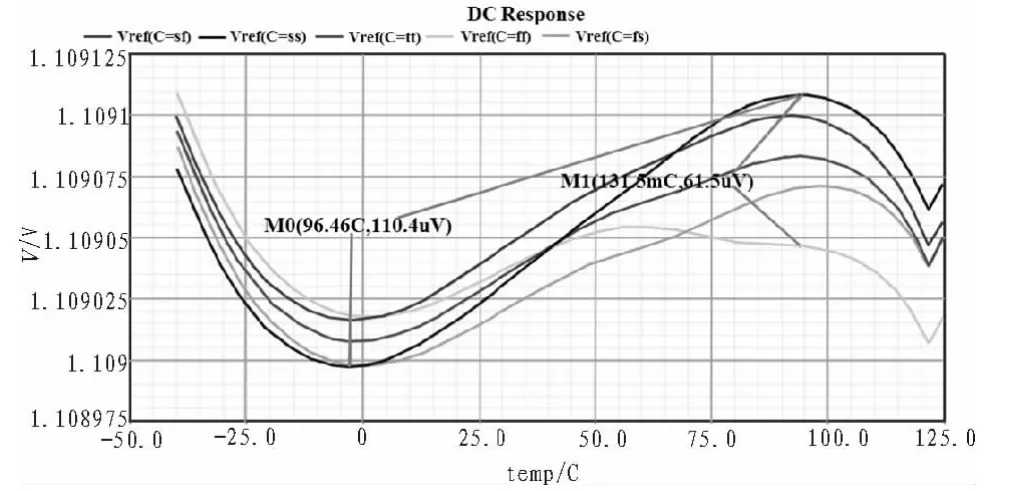
图10 不同corner下，VREF随温度变化曲线Fig.10 VREF vs Temperature at different corners

5 结 论

本文设计实现了一种适用于微弱医学心电信号放大电路的带隙基准电压源。为了获得良好的温度特性，在低温范围内，利用两个工作在不同电流密度下的pnp管之间ΔVBE含有TlnT项，来补偿VBE的温度高阶项。而在高温范围内，由于低温范围温度补偿方式存在一定的误差，本文提出了一种新型的高温温度补偿方式来修正该误差，即利用pn结反向电流随温度升高而变大的特性，在高温范围内吸取输出端的电流，从而减小输出电压。仿真结果证明，这两种补偿方式的结合能够很好的对温度系数进行补偿，在-40~125℃范围内，获得了0.445~0.604 ppm/℃的温度系数。同时本文采用了预稳压器来提高电路的PSR，使得PSR在10 Hz时为-127.5 dB，在100 kHz时达到-63 dB。在3.6 V电源电压时，带隙电路消耗的功耗在36 μW左右。本文设计的带隙基准电路还有对工艺免疫的特点，工艺差别最大使输出电压产生61.5 μV的变化。

图11 不同corner下，VREF随温度变化的温度系数Fig.11 TC vs Temp at different corners

[1]Tsividis Y P.Accurate analysis of tempera-ture effects in ICVBE characteristics with application to bandgap reference sources[J].IEEE J.Solid-State Circuits，1980（SC-15）:1076-1084.

[2]Meijer G，Schmale P C，Zalinge K V.A new curvaturecorrected bandgap reference[J].IEEE J.Solid-State Circuits，1982（SC-17）:1139-1143.

[3]Shu Yuan Chin，Chung Yu Wu.A new type of curvaturecompensated CMOS bandgap voltage references[C]//Proceedings of Technical Papers of International Symposium OnVLSITechnology， System， andApplications，1991:395-402.

[4]Salminen O，Halonan K.The higher order temperature compensation of bandgap voltage references[J]. IEEE International Symposium on Circuits and Systems，1992（3）:1388-1391.

[5]J P C Cajueiro，C A dos Reis Fjlho.CMOS bandgap with base-current thermal compensation[C]//Integrated Circuits and Systems Design，2002:345-349.

[6]Leung K N，Mok P K T，Leung C Y.A 2-V 23-uA 5.3-ppm/℃curvature-compensated CMOS bandgap voltage reference[J].IEEE J.Solid-State Circuits，2003，38（3）:561-564.

[7]Stefan Marinca，Tom O'Dwyer.Curvature Correction Method for a Bandgap Voltage Reference[C]//Signals and Systems Conference， 208.（ISSC 2008）.IET Irish，2008:134-137.

[8]Yumu Hu.A 900 mV 25 μW high PSRR CMOS voltage reference dedicated to implantable micro-devices[J].IEEE J.2003:373-376.