基于稠密子团和边聚类系数的局部社团挖掘算法

罗 浪，张绍武，陈 韬

（西北工业大学 自动化学院，陕西 西安 710072）

近年来，复杂网络已在计算机科学、生物学、统计物理学、社会学和经济学等领域在内的广泛关注，并且逐步体现出了一定的应用价值。复杂网络最重要、最普遍的拓扑结构属性之一是社团结构，社团结构是指在复杂网络中那些节点之间连接非常紧密的小团体。团体内节点连接紧密，团间连接稀疏。网络社团结构的发现与分析对于了解整个网络结构、特征及功能有其重要意义，且在生物学、物理学、计算机、社会学和经济学等领域发挥的重要作用[1-3]。

目前已经提出了较多社团挖掘算法，根据删除/添加边、点准则，复杂网络社团挖掘算法一般可分分裂和凝聚二类算法，其代表性经典算法分别为GN算法[4]，FN算法[5]。GN算法通过不断删除网络中边介数最大的边对网络进行划分，时间复杂度较高；FN算法则通过模块度值变化合并网络对网络实施划分。 Wang等人[6]不断寻找最大程度改进节点局部模块度的点，将其加入社团，对网络进行社团划分。Hu等人[7]用边聚类系数替换GN算法中的边介数，提出一种基于边聚类系数的分裂算法，但该算法仍有GN算法一些缺点。Zhang等人[8]利用邻居节点与社团的连接紧密程度，不断寻找满足它要求的条件的节点，将这些节点加入社团，从而发现社团结构，该算法速度较快，但准确度不高。2011年，Liu等人[9]改进了Wang和Zhang算法，通过不断寻找与社团共享邻居数最多的邻居节点，基于局部模块度[10]划分社团。由于该算法每次仅选取一个节点加入社团，导致最后剩下的孤立节点较多，因而算法准确度不高、运算时间较长。针对文献[9]产生的孤立节点较多问题，本文提出一种基于稠密子图和边聚类系数的局部社团挖掘算法，并计算机生成网络、Zachary网络、三社团网络和美国足球俱乐部网络上进行了仿真实验验证。

1 基本概念

1.1 共有邻居数

在社团的邻居节点中，若某节点与社团C的共有邻居节点数目越多，则此节点与社团C的连接就越紧密，也就是说该点属于社团C的可能性就越大。给定一个无权无向网络G（V，E），其邻接矩阵为 A（aij），若节点 vi和 vj有边相连则 aij=1，否则aij=0。 设Ni，Nj分别为节点 vi和 vj的所有邻居节点集合。则任意两个节点的共有邻居数定义为：|Nij|=|Ni∩Nj|。如图1 所示，节点 v4的邻居节点为{v1，v2，v3，v5，v6，v7，v8}，节点 v7的邻居节点为{v4，v5，v6，v8，v9}，则节点 v4与节点 v7的共有邻 居为{v5，v6，v8}，即|N47|=3，相对于其他节点来说节点 v4与节点 v7的连接是最紧密的。而节点v3与节点v9跟任何节点都不具有共有邻居，则N39为空集，即|N39|=0。

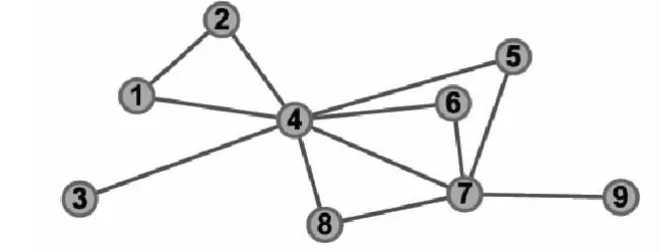
图1 简单连接图Fig.1 Simple connection diagram

1.2 稠密子团

给定一个无权无向的网络G（V，E），设网络中度最大的节点为 va，则 va的邻居节点集合为 N={v1，v2，…，vk}， 集合 N中与节点va的共享邻居数最多的节点集合为 N′={v1，…，vr}，次多的节点集合为N″={v1，…，vo}，则稠密子团定义为Cd={vx=（{va}∪N′∪N″）}。

由于稠密子团是由一个节点和它的某些邻居所组成，且连接的密集程度比较高，所以可以利用这个特性将稠密子团作为一个初始聚类团，并逐渐扩张成社团结构。

1.3 边聚类系数

在网络G=（V，E）中，假设两个节点vi和vj有一条边为eij，节点vi和vj在网络中的共有相邻节点vk，则有相邻边 eik、ejk，与eij形成一个边数为3的闭合路径即一个三角环。则复杂网络中一条边的边聚类系数[7]Cij定义为

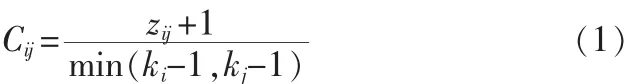
其中 ki、kj分别表示节点vi和vj的度，zij为网络中实际包含该边的三角环总数，分母为网络中包含该边的最大可能存在的三角环总数。边聚类系数Cij反映两个节点在同一个社团的可能性，Cij值越大，则这两个节点在一个社团的可能性就越大。

2 DIDE算法

DIDE算法，首先通过选取一个稠密子团作为初始聚类团，然后通过对边聚类系数和模块度的值不断扩张稠密子团，从而形成社团。实施过程如下：

1）稠密子团选取

Step 1取网络中节点度最大的节点作为初始节点；

Step 2寻找初始节点邻居节点v0；

Step 3计算v0与初始节点的共有邻居数；

Step 4将共有邻居数最多、次多的v0都加入到稠密子团中。

2）稠密子团扩张

Step 1计算稠密子团的局部模块度值 QC=Lin/（Lin+Lout），其中Lin为社团内部连接数目；Lout社团内部节点与社团外部节点连接数目；

Step 2寻找稠密子团邻居节点vi；

Step 3计算vi与稠密子团的连接紧密程度值Ui=|Eic|/di，其中|Eic|表示节点vi与社团的连接数目，di表示节点vi的度；

Step 4 若 Ui＞0.5，将 vi加入稠密子团；

Step 5计算剩余邻居节点vl边聚类系数，若该邻居节vl点与社团C相连的边聚类系数最大，则将vl加入到社团C中，形成新社团C′；

Step 6 计算 C′的局部模块度 Q′值，若 Q′-QC＜0，则将此节点从社团C′中移除；

Step 7当剩余邻居节点vl全部计算完之后C，更新社团C，并计算社团的局部模块度值QC。重复Step 2-6，直到局部模块度值QC不再变化为止；

Step 8返回1），直到找不到稠密子团为止。

3）孤立节点的加入

在所有社团都划分完之后，将孤立节点随机加入到已划分的社团中。

DIDE算法流程图如图2所示。

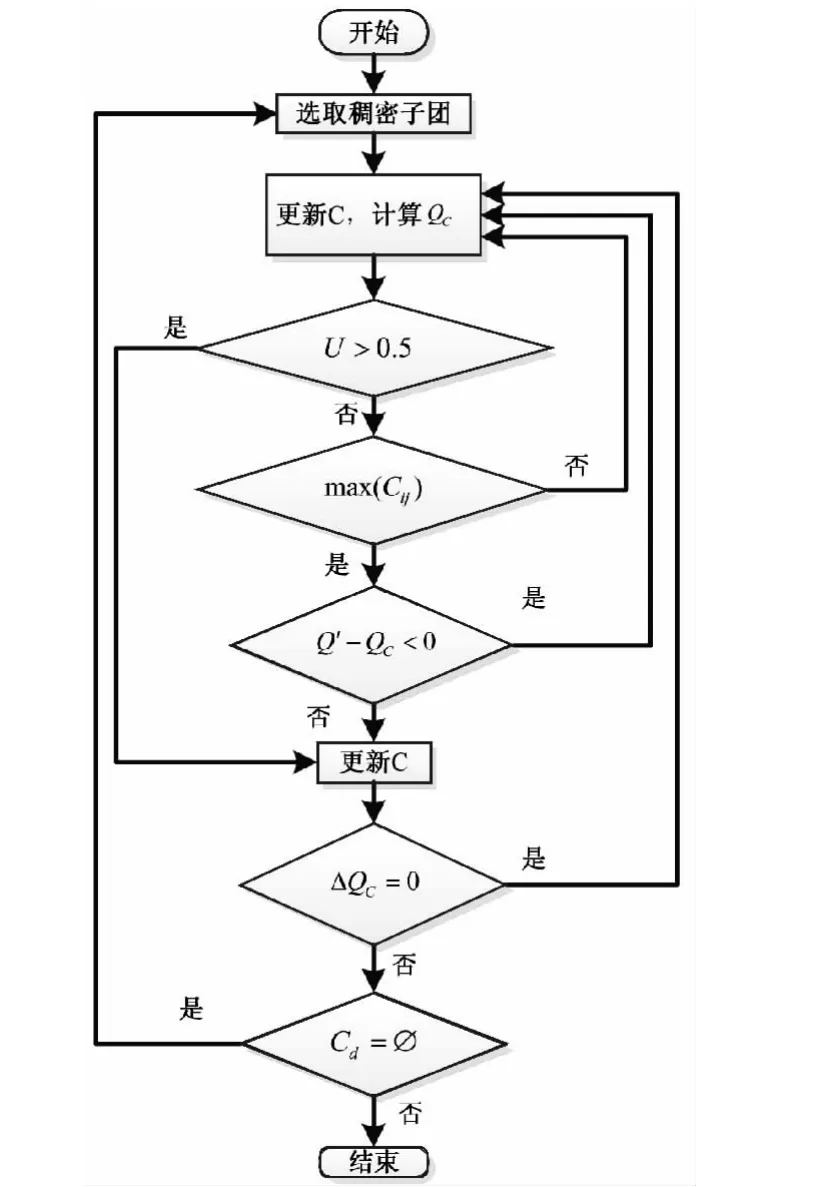
图2 DIDE算法流程图Fig.2 The flowchart of DIDE algorithm

3 实验与分析

1）计算机生成网络

首先我们在计算机生成网络上验证DIDE算法性能。计算机生成网络是由128个节点组成，分为4个社团，每个社团包含32个节点。假设每个节点与社团内部的连接数为zin，与社团外部的连接数为zout，且zin+zout=16。随着zout的不断增加，该网络的社团结构将会变得越来越模糊，当zout＞8时，则认为此时网络不具有社团结构。DIDE算法及其他7种算法（Liu、Zhang、GN、FN、SA、CPM、FEC）对计算机生成网络的划分结果如图3所示。

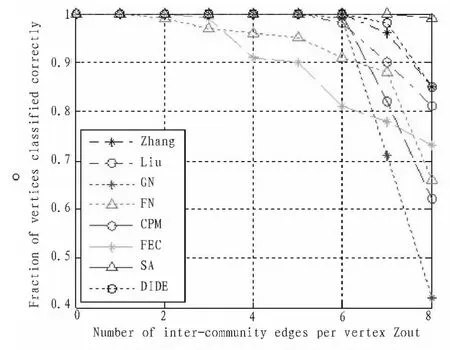
图3 8种算法聚类精度比较Fig.3 Comparison of 8 algorithms relative to the fraction of vertices classified correctly

图3可以看出，DIDE算法社团划分性能优于 Zhang、Liu、GN、FN、SA、FEC、CPM 算法。 虽然 DIDE 算法社团划分性能低于SA算法，但SA算法时间复杂度较高。SA算法的计算速度完全取决于模拟退火算法效率，但模拟退火算法收敛速度很缓慢。文献[11]中利用SA算法对一个有3885节点、7260条边的网络进行社团划分，居然花了3天时间。而DIDE的算法时间复杂度仅为O（n2），n为网络的节点数，也可以达到较高的准确度。

2）三社团网络

三社团网络是由19个节点，37条边构成了一个经典的验证网络，如图4所示。

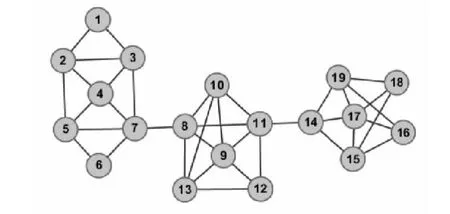
图4 三社团网络结构图Fig.4 The structure of three groups network

DIDE算法对该网络社团划分过程如下：首先从度最大的节点v7、节点v8、节点v9和节点v17中随机选取一个节点作为初始节点。我们取节点 v17，形成的稠密子团 Cd1={v14，v15，v17，v19}，利用边聚类系数以及局部模块度值扩张为社团C1={v14，v15，v16，v17，v18，v19}，它的局部模块度 Q 值为 0.916 7。 然后选择节点形成稠密子团 Cd2={v4，v5，v6，v7}，最后扩张为社团 C2={v1，v2，v3，v4，v5，v6，v7}，它的局部模块度 Q 值为 0.7857。 同理可以得到以节点为初始节点的稠密子团 Cd3={v8，v9，v10，v11，v12，v13}，即 局 部 模 块 度 Q 值 为 0.923 0 的 社 团 C3={v8，v9，v10，v11，v12，v13}。DIDE算法在三社团网络上的划分结果与实际网络结构完全一致。

3）Zachary网络

Zachary网络为美国一所大学空手道俱乐部成员间相互社会关系网，该网络由34个节点和78条边组成，节点代表俱乐部成员，而边代表俱乐部成员之间的关系。Zachary网络上， DIDE、Zhang、GN、Liu、FN 算法社团划分结果如表 1。 表 1结果表明：DIDE和Liu算法的划分效果优于 Zhang、GN和FN算法，与实际网络社团结构完全一致。

图5为DIDE算法对Zachary网络的社团划分结果。图中菱形社团的局部模块度Q值为0.782 5；三角形社团的局部模块度值Q为值0.708 5。

表1 五种算法对Zachary网络的社团划分结果Tab.1 The results of detecting Zachary network community by 5 algorithms

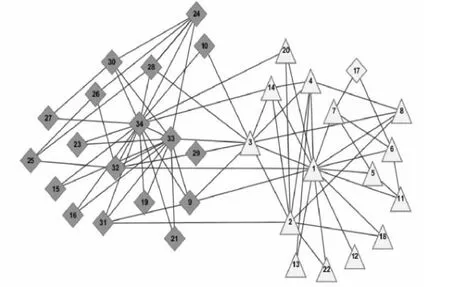
图5 DIDE对Zachary网络划分结果图Fig.5 Tthe result of detecting Zachary network community by DIDE

4）美国足球俱乐部网络

美国足球网络是美国大学生足球联赛得出的一个复杂网络，网络中的节点代表一只足球队，边代表两个球队之间进行过一场比赛，它一共包含115个节点及616条边。联赛中存在若干联盟，每个节点都属于其中一个联盟，联盟内部球队间比赛次数多于联盟间球队进行的比赛次数。这115支球队共存在12个联盟。

表2是DIDE算法与其它算法对美国足球俱乐部网络社团划分结果对比，从表2中结果表明，在分团数方面DIDE与Liu的算法分为12个团要优于Zhang算法以及 GN、FN算法。而在正确率方面，同为12个分团数，由于DIDE算法在循环中同时加入多个节点，从而减少孤立节点，所以要比Liu算法准确度更高。

DIDE算法对美国足球俱乐部网络的社团划分结果如图6所示，表3为12个联盟球队编号以及每个联盟的局部模块度Q值。

表2 五种算法对美国足球俱乐部网络社团划分结果Tab.2 The result of detecting American football club network community by 5 algorithms

在美国足球俱乐部网络中，DIDE算法一共错分了9个节点（43，59，60，64，81，83，91，98，111），由于实际原因，这些节点所代表的球队跟外联盟球队比赛次数要多于联盟内部比赛次数导致了DIDE算法出现了一些错分情况，但是DIDE算法仍能够达到较高的划分正确率。

4 结 论

本文通过定义稠密子团，利用边聚类系数以及局部模块度不断扩张稠密子团，提出一种基于稠密子团和边聚类系数的局部社团挖掘算法（DIDE）。DIDE算法以稠密子团这种连接密集程度比较高的聚类团为种子，在一定程度上减少算法时间复杂度，循环过程中同时加入多个节点以减少孤立节点数目，从而提高了社团划分的准确性。在计算机生成网络及其他几个现实经典网络（三社团网络、Zachary网络、美国足球俱乐部网络）上，通过与Liu、Zhang、GN、FN算法进行对比，实验结果表明 DIDE算法性能优于Liu、Zhang、GN、FN算法，比Liu方法更适合较大规模网络社团划分。

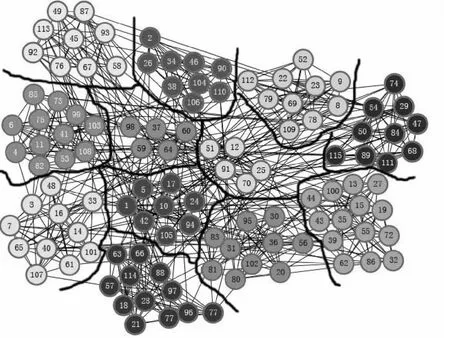
图6 DIDE对美国足球俱乐部网络划分结果图Fig.6 The result of detecting American football club network community by DIDE

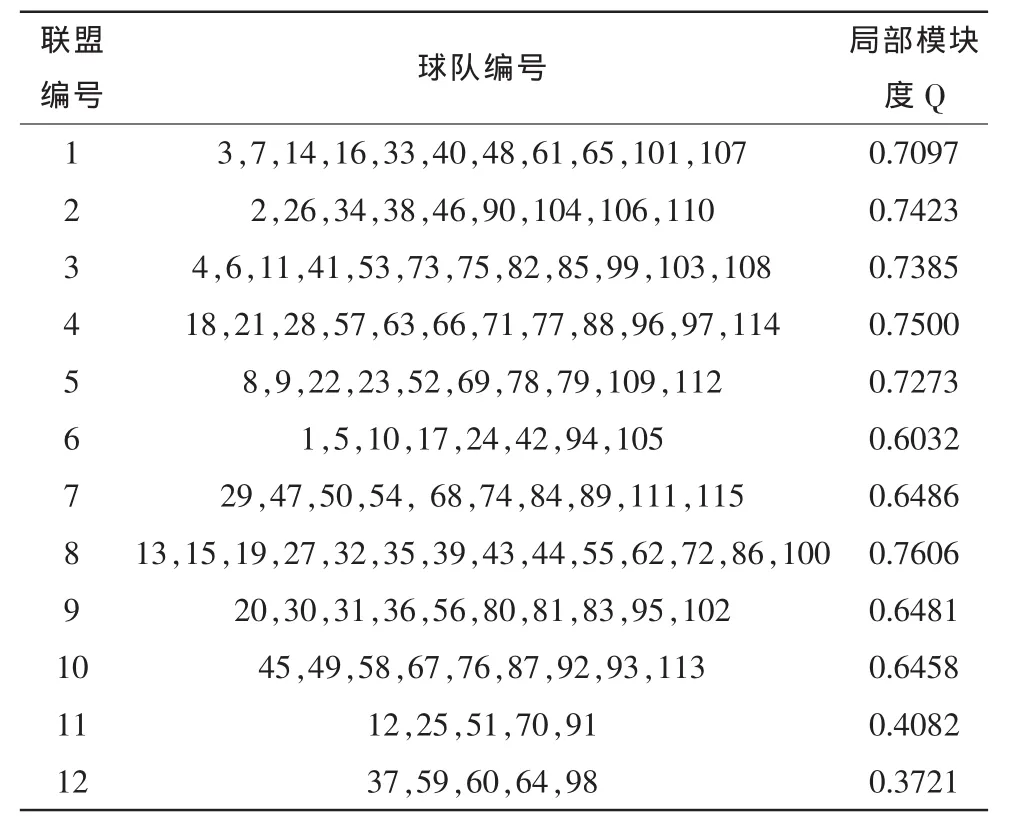
表3 DIDE算法得到的联盟球队编号及局部模块度值Tab.3 Union team numbers and local modularity value by DIDE

[1]ALBERT R，JEONG H，BARABSI A L.The diameter of the World Wide Web[J].Nature，1999（401）:130-131.

[2]SCOOT J P.Social network analysis:a handbook[M].London:Sage Publications，2000.

[3]HOLME P，HUSS M，JEONG H.Subnetwork hierarchies of biochemical pathways[J].Bioinformatics，2003，19（4）:532-538.

[4]NEWMAN M E J，Girvan M.Finding and evaluating community structure in networks.Phys.Rev.E，2004 （69）:02611.

[5]Newman M E J.Fast algorithm for detecting community structure in networks.Phys.Rev.E，2004（69）:066133.

[6]WANG Xu-tao，CHEN Guang-rong，LU Hong-tao.A very fast algorithm for detecting community structures in complex networks[J].Physica A，2007，384（2）:667-664.

[7]胡健，杨炳儒.基于边聚集系数的社区结构发现算法[J].计算机应用研究，2009，26（3）:858-859.

HU Jian，YANG Bing-ru.Community structure discovery algorithm based on edge clustering coefficient[J].Application Research of Computers，2009，26（3）:858-859.

[8]ZHANG Da-wei，XIE Fu-ding，ZHANG Yong，et al.Fuzzy analysis of community detection in complex networks[J].Physica A:Statistical Mechanics and its Applications，2010，389（22）:5319-5327.

[9]刘微，张大为，谢福鼎，等.基于共享邻居数的社团结构发现算法[J].计算机工程，2011，37（6）：172-174.

LIU Wei，ZHANG Da-wei，JI Min，et al.Community structure detection algorithm based on number of shared neighbors[J].Computer Engineering，2011，37（6）:172-174.

[10]Clauset A.Finding local community structure in networks.Phys[J].Rev.E， 2005（72）:026132.

[11]杨博，刘大有，Liu Ji-ming，等.复杂网络聚类算法[J].软件学报，2009，20（1）:54-56.

YANG Bo，LIU Da-you，LIU Ji-ming，et al.Complex network clustering algorithms[J].Journal of Software，2009，20 （1）:54-66.

[12]王立敏，高学东，宫雨，等.基于相对密度的社团结构探测算法[J].计算机工程，2009，35（1）:117-119.

WANG Li-min，GAO Xue-dong，GONG Yu，et al.Community structure detection algorithm based on relative density[J].Computer engineering，2009，35（1）:117-119.

[13]GIRVAN M，NEWMAN M E J.Community structure in social and biological networks[J].Proceedings of the National Academy of Sciences of the United States of America，2002，99（12）:7821-7826.

[14]POTHEN A，SIMON H，LIOU K P.Partitioning sparse matrices with eigenvectors of graphs[J].SIAM Journal on Matrix Analysis and Applications，1990，11（3）:430-452.