蓄热式加热炉的温度智能控制

陈志刚 廖 宁

（华菱涟源钢铁集团有限公司 信息自动化中心，湖南 娄底417009）

0 引言

某棒材厂加热炉为蓄热式加热炉，通过混合煤气和空气的混合燃烧使炉体内的钢坯加热。 炉体分为预热段、加热段、均热段。 三段分段分散自动换向，各段换向控制完全相同且各自独立。 目前在加热炉炉温自动控制中，传统的方法是根据炉温偏差及煤气、空气实际流量采用双闭环PID 控制策略。由于加热炉是一种具有强耦合、纯滞后、大惯性、慢时变和干扰因素很多等特点的典型非线性系统。 很难用数学方法建立精确的数学模型，因此采用传统的温度流量双闭环PID 控制理论和方法导致了炉温波动大、超调严重、升降温速度慢，很难达到良好的控制效果[1]。模糊控制技术不依赖于精确的数学模型，对参数的变化不敏感，适应性强，具有很好的鲁棒性。但是常规的模糊控制器也存在一些不足，存在稳态误差较大，系统的上升特性不理想、超调大、调节时间长、甚至产生振荡等。 产生这些缺点的主要原因是常规的模糊控制器在结构上过于简单，在设计时人的主观因素占的比例较大(模糊控制规则由人的经验确定)，而且一旦模糊规则确定就不再改变等。 为了改善模糊控制器的动态特性和减小稳态误差，本文采用一种基于参数自调整模糊控制器: 即通过在线调整参数改善系统的响应速度，提高精度。同时为了保证煤气燃烧过程中的煤气流量和空气流量达到最佳空燃比，采用改进型双交叉限幅控制的方案，以达到最佳燃烧的要求。组成了蓄热式加热炉温度控制系统的参数自调整模糊控制器和改进型双交叉限幅控制相结合的方法。其中参数自调整模糊控制器作为主调节器，计算出煤气流量的增加或减少值，相当于温度控制器。改进型双交叉限幅控制进行煤气和空气流量控制。各段的温度控制系统控制原理如图1 所示。 图中Tsp 代表炉温设定值，T 代表炉温反馈值。

图1 加热炉温度控制系统原理图Fig.1 The principle scheme of heating furnace temperature control system

加热炉温度控制系统由上位机、下位机和被控对象组成。 上位机装有WINCC 监控软件和Step7 编程软件,完成系统的监控和控制程序设计。 下位机选用西门子S7-400 PLC 作为控制器。 控制算法采用Step7 编程软件的梯形图(LAD)编程语言来实现。

1 改进型双交叉限幅控制

按照热工理论的要求，必须保持适当的空燃比，才能保证混合煤气的充分燃烧。 存在一个热损失最小、热效率最高的低空气过剩燃烧范围，称之为最佳燃烧带。 最佳燃烧带所对应的空气过剩系数u 介于1. 02-1.10 之间。 由于煤气与空气调节回路的响应速度不一致，煤气热值不稳定，以及烧嘴特性等的变化，这种配比关系往往无法保证，通常采用双交叉限幅的方法。图2 示出了双交叉限幅控制的原理[2]。其中a1=0.03,a3=0.05,us=1.05 (us-额定空气过剩系数)，则1.02≤u≤1.10,即在最佳燃烧区，一般取a1=a2,a3=a4。

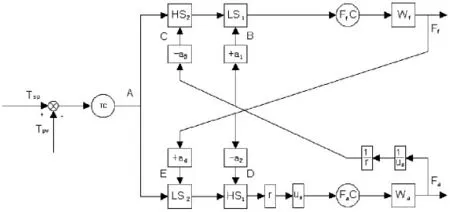
图2 双交叉限幅燃烧控制系统Fig.2 Double cross limited range combustion control system

双交叉限幅虽然有效控制了动态空燃比，缺点是限幅牺牲了系统跟踪负荷变化的速度，降低了系统的响应速度；另外在实际应用中易使控制系统出现震荡现象。 为了提高响应速度，本系统采用改进型双交叉控制方案，改进型双交叉方法将限幅系数a1～a4，以及空气过剩系数u,设为可根据温度偏差自动调整，以便在温度偏差较大时减弱或取消限幅功能，以兼顾响应速度和空燃比的稳定与合理。

2 参数自调整模糊控制器的设计

2.1 常规模糊控制器的构成

2.1.1 常规模糊控制器的结构

本例选择模糊控制器的输入变量为误差e 及误差的变化ec，输出变量△u 为控制量的变化量，相应的模糊集为E, EC, △U，是一个双输入单输出的二维模糊控制器[3]。

对误差E、 误差变化EC 及控制量△U 的模糊集及其论域定义如下:

E 的模糊集为:{NB, NM, NS, ZO, PS, PM，PB}

EC 和△U 的模糊集均为:{NB, NM, NS, ZO, PS, PM，PB}

E 和EC 的论域均为:{-6，-5，-4，-3，-2，-1,0,1,2,3,4,5,6}

△U 的论域为:{-7，-6，-5，-4，-3，-2，-1,0,1,2,3,4,5,6,7}

输入量e 在的实际变化范围[a,b]转化为模糊论域中[-n,+n]上，记为e*，转化公式为：

式中n 表示量化等级，a,b 分别为e 的下限值，上限值。 计算出的值e*如果不是整数，可以把它归一化为最接近于e*的整数值。

偏差e,偏差变化量ec,输出△u 均选择三角形函数来确定语言值的隶属度函数。

2.1.2 模糊控制规则

根据操作工人的经验，加热炉炉温调节对象可根据系统的误差E及误差的变化EC 来消除误差。 相应控制规则可用如下模糊条件语句来描述:

if E= NB and EC= NB or NM or NS or ZO then △U= PB

经过总结和归纳得到23 条控制规则， 相应可构成一个模糊控制规则表，如表1 示。

表1 模糊控制规则表Tab.1 The rules table of fuzzy control

2.1.3 建立模糊控制表

采用第一类推理方式，亦称Mandani极小运算法。 来确定模糊关系Rl(l=1,2,…,23)。

模糊关系Rl=RAl∩RBl(l=1,2,…23)

第一条语句确定的控制规则为

if E= NB and EC= NB or NM or NS or ZO then △U= PB

由第1 条语句所确定的模糊关系可用下式写出，即

R1=(NBE×PB△U)∩[(NBEC+NMEC+NSEC+ZOEC)×PB△U]=RA1∩RB1

可以求出RA1和RB1。 同理，其它控制语句的模糊关系RAl和RB1（l =2,3,…23）也可以求出，按照如下关系式可分别求出RA和RB。

在求出模糊关系R 以后，可以由合成推理方法求解输出控制量的模糊值矢量，控制器总的输出控制量按下式求得。

表2 模糊控制查询表Tab.2 Polling list of fuzzy control

计算e，ec 在各等级在隶属度函数值等于1 上的控制量， 为了提高控制的精度，保证次要信息不被丢失，本文采用加权平均法解模糊，将控制量由模糊量变为精确量，最后制成如表2 所示的控制表。

用PLC 实现模糊控制时，将此表的数据存入模糊控制功能块中，控制程序将e,ec 的输入信号进行模糊化后，查表即可得出对应输入的精确控制量。 如E=+2,EC=-1,查表可得△U=-0.28。 经过现场反复调试，此项目中加热段ku取3000，ku 表示控制控制量的比例因子，即为煤气流量调节系数。 其它段ku根据现场煤气流量大小适当选取。

2.2 模糊控制参数调整的设计原理

模糊控制中的比例因子ke、kec和ku对模糊系统的稳态特性和动态特性均有较大的影响。 一般说，若ke大，则系统上升速率大，但过大将使系统产生较大超调，调节时间增加。 若ke很小，则系统上升速率慢，快速性查。ke还直接影响系统的稳定品质，ke越大，稳态误差越小，调节死区越小。若kec越大，系统上升速率小，过渡时间长。若kec越小，系统上升速率增加越大，但kec 太小会产生很大超调和振荡。 ku对系统响应的上升和稳定阶段有不同的影响。 上升阶段，ku越大， 上升越快，但容易引起超调；ku小，则系统反应慢。在稳定阶段，ku过大会引起振荡。 由此可以发现，模糊控制和同常规控制一样，其动态、静态特性之间存在一定的矛盾， 采用固定的参数难于同时获得满意的动态、静态特性。 因此为了改善模糊控制器的，常需要根据系统的误差和误差变化等信息，对控制器的参数进行在线修正。改善动态性能时，同时调整三个参数会使控制算法过于复杂， 因为ke、kec和ku三者互相牵制，从控制器的结构看， 调整ku因果关系明确， 而且最终也能起到调整ke、kec的作用。 因此本项目采用离线整定ke、kec，在线调整ku的方法[4]。

2.2.1 改善稳态性能

模糊控制系统当E 和EC 处在0 等级范围内时. 系统不会产生任何旨在消除误差的动作控制“死区”，解决办法是放大误差和误差变化

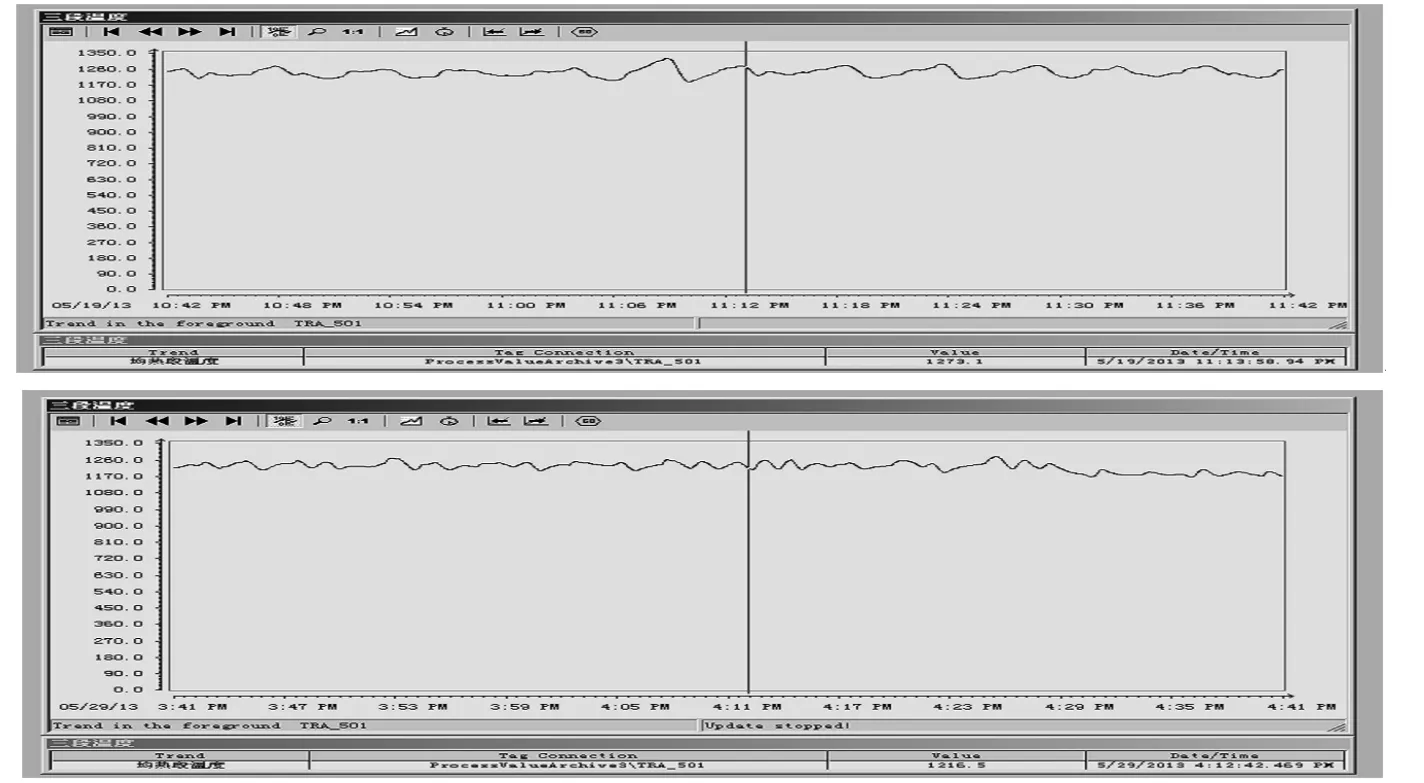
图3 炉温控制效果对比图Fig.3 The effective compare scheme of furnace temperature control

量化因子ke、kec，即在小偏差时增加分档间隔，从稳态性能看，ke、kec愈大愈好，但ke、kec增大将加激系统的动态过程，使超调量加大。 为保证控制的质量，应适当减小控制比例因子Ku。

2.2.2 改善动态性能

根据系统误差变化的典型曲线，当e 较大时，为了迅速消除误差，希望控制作用大些，即ku要取大些。 当e 接近稳态区域时， 如果e 与ec 的变化趋势相同， 为使e 迅速收敛，ku要取稍大些；如果e 与ec 的变化趋势相反，为使e不至于冲过设定值而引起新的波动，ku要取稍小些。 可以总结出如下3 条控制规则：

R1: If |e|＞βR Then K'u=αKu

R2: If |e|＜δ and e*ec＞0 Then K'u=(1+γ)Ku

R3: If |e|＜δ and e*ec＜0 Then K'u=(1-γ)Ku

式中：e、ec——误差和误差变化；

δ——允许误差变化的范围；

β、α、γ——均为常数，由经验确定；

R——为给定值；

Ku——常规模糊控制中的比例因子。

3 控制效果展现

基于参数自调整模糊控制器和改进型双交叉限幅控制相结合的蓄热式加热炉温度控制系统自2010 年11 月投入以来至今，加热炉各段炉温较以前大为稳定，完全满足了用户对炉温的要求，炉温控制在设定值的±20℃之内。大大减轻了操作人员的劳动强度。图3 为原人工手动控制和采用参数自调整模糊控制器和改进型双交叉限幅控制相结合均热段炉温的对比曲线。上图中的曲线为原人工手动控制均热段炉温的历史趋势曲线，下图中的曲线为采用参数自调整模糊控制器和改进型双交叉限幅控制均热段炉温的历史趋势曲线。对比可以发现下图中的曲线比上图中的曲线要平缓很多。

4 结束语

针对加热炉控制对象存在的非线性、时变、大滞后系统往往难以获得其精确的数学模型的特点，本文在充分分析加热炉燃烧过程和炉温变化的基础上，提出一种基于智能控制策略的加热炉燃烧模型。 将双交叉限幅控制和参数自调整模糊控制有效结合，充分发挥了二者的优点。 本控制算法应用到棒材厂，经过长时间的运行效果证明了该控制系统方案是合理的。

［1］曹卫华,吴敏.基于阀门开度的加热炉模糊专家控制[J].吉林大学学报,2004,34(3):475-478.

［2］茅忠明.应用STD 工控机实现加热炉双交叉限幅燃烧控制[J].计算机应用,1994(5):44-46.

［3］张东波,朱建林.用于加热炉的专家模糊温度控制器[J].机电工程,2002,19(1):51-56.

［4］诸静.模糊控制理论与系统原理[M].北京:机械工业出版社,2005,8.