基于评估基准期的既有梁桥时变可靠度评估方法*
王晓明 石雪飞 阮 欣
(长安大学公路学院桥梁工程研究所1) 西安 710064) (同济大学桥梁系2) 上海 200092)
0 引 言
随机系统的描述与建模是时变可靠度问题求解的关键.随机变量模型是被规范[1]采用、具有很强实用性的描述模型.抗力最小值法[2]分别采用评估时段内抗力的最小值分布与荷载效应的最大值分布来描述随机系统,进行可靠度分析.赵国藩[3]的抗力加权平均法将结构不同时段的失效转变为串联可靠度问题,将评估时段等分为m份并加权平均用于综合反映基准期内结构抗力的变化历程.田周松[4]把“规定时间”定义为车辆荷载统计的基准时段(1a),从而时变可靠度可理解为结构每年在规定条件下不失效的概率,相应的评估荷载采用截口分布,目标可靠指标调为5.15,但是这种将时间域离散开来的做法,忽略了各时间段活荷载的相关性,降低了极值荷载的出现几率.上述研究聚焦于2点:结构抗力的变化与评价参考时间的变化,本文将其归纳为时间域整体法、时间域分割法,二者的区别与联系见表1.但是,前述方法都是通过单次分析来评价未来服役期的总体安全程度,属于静态评估,缺乏对结构可靠性变化的反映,也无法考虑数据更新的影响.为了解决这一不足,掌握结构功能可靠度的实时变化,在文献[5-7]规范可靠度方法的基础上,不断更新抗力,在多个时间点反复进行评估来绘制功能可靠度的变化曲线,属于动态评估.因此,基于随机变量模型,采用时间域整体思路的动态评估方法已日渐成为时变可靠度的主要计算方法.

表1 随机变量模型方法的分类与特点
基准时间参数对时变可靠度的分析具有明显影响.在反映安全性的承载能力极限状态分析中,抗力、荷载、目标可靠指标都是基准时间参数的函数[9],且该参数在动态评估中随着评估时间的前移而不断改变.对安全性进行时变可靠度评估的国内外主要研究中,Frangopol与贡金鑫考虑了抗力随时间的改变,都采用动态评估的思路对随机变量模型不断求解,获得安全可靠指标在寿命周期内的演变.但这些研究中,车辆荷载效应仍然采用设计基准期,既没有考虑基准时间参数的影响,又忽略了动态评估中该时间参数随着时间前移的改变.出现这一问题根源是:将耐久性评估中的时变可靠度方法,直接惯性式的照搬到结构承载安全性评估中来.在耐久性评估中,参数t的作用只限于对侵蚀量的影响;而安全性评估中,相类似的需要在抗力计算中考虑时间的影响,此外仍需要在车辆荷载效应及目标可靠指标的确定中考虑基准期的影响,而基准期是随着评估时间的前移而不断改变的,其中时间对车辆荷载效应的影响主要体现在基准期对最大值分布的影响.因此,在安全性的时变可靠度评估方法中,如何考虑评估基准期的影响尚需要进一步的研究.
1 评估基准期的确定方法
评估基准期是指在进行结构可靠性评价时,考虑持久状况下各项基本变量与时间关系所取用的基准时间参数.
等超越概率准则是确定评估基准期的基本方法.
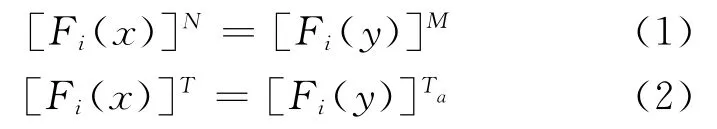
式中:Fi(x)为截口荷载随机变量的概率分布函数.故可确定评估基准期Ta可表达为

等超越概率准则是在承认结构设计荷载基准期确定是合理的基础上,采用类比法来确定评估荷载基准期的方法.
然而实际使用中,问题的关键是上式右侧各变量如何确定?上述再服役期M是个预期值,由决策者主观和经验决定.它的真实值是结构实际的可以继续服役年限,因此可以通过退化模型来预测该值,由于再服役期M是确定评估荷载的必要参数,故这是一个迭代[10]的过程.
目前规范[11]只明确给出设计基准期T=100 a,而对于设计使用期则没有给出,已有研究的设计使用期N的取值方法有2种:(1)通过调研统计,陈艾荣等[12]通过调研统计给出,钢筋混凝土主梁的设计使用期建议值为N=60a,钢筋混凝土墩柱设计使用期建议值为N=70a.该方法推荐值可信度高,具有普遍性,但缺乏针对性;(2)取设计基准期[13],直接假设N=T=100a.该方法简便易行,但不易区分基准期和使用期的概念差异.
本文根据使用期的定义知,N即结构实际的使用年限,可根据退化模型的预测由式(4)确定
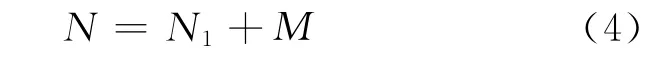
式中:N1为已服役年数已知;M 为可再服役期.因此该方法需要迭代获得.本文给出的式,既具有针对性,又符合使用期的概念,具有准确性.不足之处就是需要迭代计算,不如上述2种方法简便.
2 给定评估基准期的车辆荷载效应模型
根据规范GB/T50286-1999中设计基准期荷载效应的计算思路,评估基准期与设计基准期荷载效应最大值分布的关系可表示为

式中:FTa(x),FT(x)分别为评估基准期Ta和设计基准期T内的最大值分布函数;Fi(x)为荷载效应随机过程的截口分布.
对于一般运营状态,将设计基准期内最大分布的效应FT(x)代入式(5)中,同时考虑到设计基准期T=100a,可得评估基准期Ta所对应的最大值分布

将超越概率分别代入式(6)与FT(x)中,计算对应的分位值荷载.按照等超越概率准则,前者比后者,则得一般运营状态下活载效应修正系数λTa
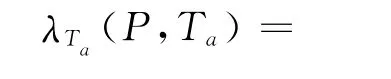

式中:P为不被超越概率,通常取95%(即超越概率为5%).
同理,可以得到密集运营状态下的修正系数如下
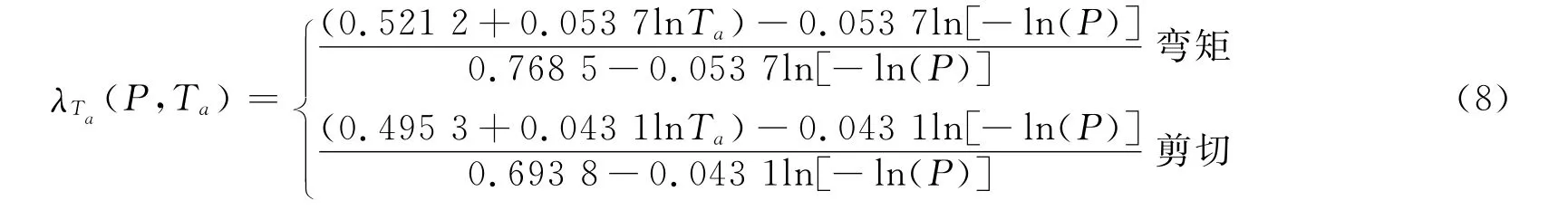
根据式(8),(9),不同评估基准期内活载效应修正系数见图1.可见,评估基准期下的车辆荷载效应较设计荷载有较明显变化,特别是当评估基准期小于20a(Ta/T=1/5)时,评估荷载下降率剧增.
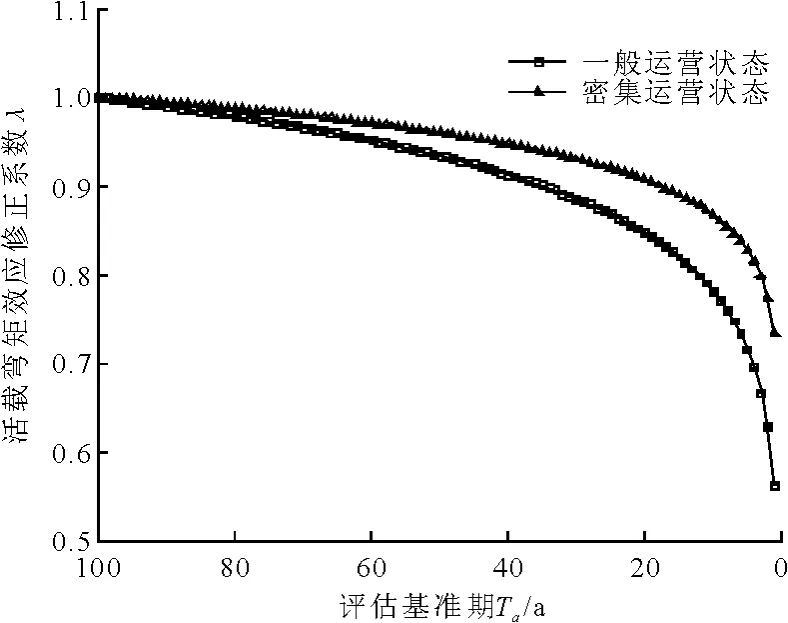
图1 弯矩车辆荷载效应修正系数
3 给定评估基准期的目标可靠指标计算方法
寿命期的目标可靠指标是根据人们可以接受的年失效概率制定的[14],是基准期的函数,换算原则可称之为等年失效概率法.
本文根据年失效概率相等准则,建立基于给定评估基准期的目标可靠指标确定方法如下.
设年目标失效概率为P1,各年的P1相互独立,则设计基准期T内的目标失效概率PT为

上式即为年失效概率相等准则.引入失效概率与可靠指标的关系,则评估基准期Ta所对应的目标可靠指标为
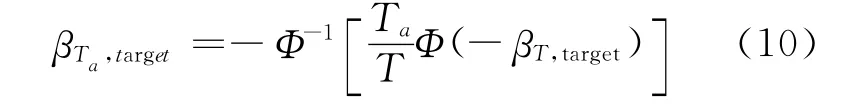
按照规范,设计基准期T为100,二级延性破坏结构的βT,target为4.2,代入式中可得不同评估基准期的目标可靠指标,见图2.可见,评估基准期对应的目标可靠指标在4.20~5.15的范围变化,当Ta=100~20a时,βTa,target=4.2~4.5,几乎不变;当评估基准期小于20a(Ta/T=1/5)时,评估荷载上升率剧增.

图2 评估基准期的目标可靠指标
4 算 例
某13m简支空心板桥,设计荷载为公路二级,经计算最不利板的荷载横向分布系数为0.25.该桥处于一般大气环境,材料退化机理以混凝土碳化为主.应用附录中的退化模型,确定该桥100a内抗力退化状况见图3.

图3 抗力退化(尺寸单位:cm)
采用本文方法确定该桥的承载能力剩余使用寿命.图4中各比较方法的意义表述如表2.方法A~C中,可再服役期取M=100~1a;方法D采用本文建立的步骤,M由迭代确定.

表2 计算剩余寿命的各方法

图4 各方法下的剩余寿命
首先,由图4可见,方法A~C的可靠指标曲线与目标β曲线基本一致,只是在尾部差异增大,目标β曲线差异增加的更为明显.这说明相对设计基准期T=100a,当功能β曲线与目标β曲线在前期及中期相交时,各方法预测的寿命差异较小;而当两曲线在后期相交时,各方法给出的剩余寿命差异将明显增大,此时再使用概念不严谨的方法将造成较大误差.
其次,方法A,B,D确定的剩余寿命都是52a,方法C为51a:(1)方法B之所以与方法D结构接近,是由于该桥的模型预测值正好与方法C中设计使用期的采用值十分相近(分别为52和60a);(2)就本例而言,方法A与方法D的结果一致,这也正是概念很不严谨的规范方法能够广泛使用的一个原因,差异不大的现象掩盖了概念明确的重要性.但是,当β与目标β交叉点出现在尾部时,各种方法的差异会逐渐增大(调整m、抗力值来实现);或者,当退化曲线形状改变时,也不会出现这样的接近.再者,当评估指标从β变为失效概率时,将充分体现出来;(3)方法C低估了剩余寿命,说明评估中用设计基准期作为设计使用期是不合理的.
最后,当只考虑荷载系数的变化,而不考虑目标可靠度的变化(βtarget恒为4.2)时,结果分析如下:方法B确定的剩余寿命都是52a,方法C确定的为53a,而方法D将是60a左右.这说明:必须采用与评估基准期对应的目标β,否者结果是不正确的.
综上,设计规范方法在一定条件下能够较准确给出剩余寿命,但是随着功能β曲线与目标β曲线交叉时机、功能β曲线下降趋势、评估指标的改变,其结果将存在较大误差.这是由于设计规范方法的时间域与评估现状不匹配造成的.因此,基于评估基准期的剩余寿命预测方法概念正确,思路清晰,是正确预测结构寿命的有效方法.
5 结束语
基于现行可靠度标准的逻辑体系,针对在役桥梁退化的现象,站在桥梁管养的立场,以服务于动态制定运营期桥梁管养策略为目标,建立了基于评估基准期的时变可靠度评估实用方法.算例分析表明,由于设计规范方法的时间域与评估现状不匹配,采用设计规范方法的剩余寿命分析只在一定条件下适用,多数情况下其结果将存在偏差.本文建立的基于评估基准期的剩余寿命预测方法概念正确,是分析结构寿命的有效方法.
[1]交通部公路规划设计院.GB/T50283-1999公路工程结构可靠度设计统一标准[S].北京:中国计划出版社,1999.
[2]杨跃新.混凝土连续梁桥的时变可靠度评定与寿命预测[D].哈尔滨:哈尔滨工业大学,2008.
[3]赵国藩,金伟良,贡金鑫.结构可靠度理论[M].北京:中国建筑工业出版社,2000.
[4]田周松.混凝土梁桥时变可靠度计算方法研究及专用软件开发[D].上海:同济大学,2009.
[5]李生勇,张 哲,贡金鑫.基于时变可靠度混凝土结构耐久性设计方法[J].工业建筑,2007,37(8):77-81.
[6]BOCCHINI P,FRANGOPOL D M.Generalized bridge network performance analysis with correlation and timevariant reliability[J].Structural Safety,2011,33(2):155-164.
[7]OKASHA N M,FRANGOPOL D M.Computational platform for the integrated life-cycle management of highway bridges[J].Engineering Structures,2011,33(7):2145-2153.
[8]交通部公路规划设计院公路桥梁可靠度研究课题组.公路桥梁可靠度研究[R].北京:交通部公路规划设计院,1994.
[9]欧进萍,刘学东,王光远.现役结构安全度评估的环境荷载标准研究[J].工业建筑,1995,25(8):11-16.
[10]索清辉,钱永久,伍建强,等.既有结构已服役荷载对可靠度评估结果的验证影响[J].计算力学学报,2007,24(3):323-327.
[11]中华人民共和国行业标准.JTG62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:中国计划出版社,2004.
[12]陈艾荣,王玉倩,吴海军.桥梁结构构件设计使用寿命的确定[J.同济大学学报:自然科学版,201038(3):317-322:
[13]吕颖钊,任 伟,贺拴海.基于评估荷载发生概率的在役混凝土桥梁可靠度分析方法[J].路交通科技,2008,25(6):60-64.
[14]RACKWITZ R,JOANNI A.Risk acceptance and maintenance optimization of aging civil engineering infrastructures[J].Structural Safety,2009,31(3):251-259.

