基于传声损失的复合材料结构优化研究＊

陈炉云 张裕芳

（上海交通大学船舶海洋与建筑工程学院 上海 200240）

0 引 言

复合材料因其优良性能广泛应用于隔声材料.王旌生等［1］对复合材料的声学特性问题进行了系统论述.陈美霞等［2］采用有限元和边界元方法分析平板结构振动和声辐射，并对比分析了流体特性对声辐射特性的影响.李海涛等［3］应用声传递矩阵法推导多层结构的反射、透射系数计算公式，分析材料参数、背衬形式、声入射角度对结构声学特性的影响.黎胜等［4］对比复合材料层合板铺层厚度和角度等参数对声传输的影响，指出复合材料铺层设计中需注意的问题.洪明等［5］根据Zig－Zag模型，运用有限元和边界元理论对夹层板结构的振动和声传输特性数值模拟研究.K·达内什柔等［6］建立了考虑横向剪切变形的复合材料圆柱壳的声传输分析模型.Lee［7］利用改进声传输矩阵来进行多层材料声传输损失特性预测分析.Legault等［8］以结构重量最小化为目标，开展声传输问题的理论和实验研究.Wang等［9］在考虑了剪切变形基础上，对层合板的声传输问题开展了研究.Xin等［10］对流体载荷下的带肋骨的层合板的声传输问题开展了研究.对于复合材料的结构优化问题，李烁等［11］采用神经网络响应面法进行复合材料的结构优化设计.Lee等［12］应用多目标进化算法对多层复合材料进行分析.Xu等［13］研究了复合材料的声学特性，并进行开展结构拓扑优化.Denli等［14］对夹芯复合材料的声辐射优化问题进行了研究.

本文对复合材料层合板在低频段下声波斜入射声传输问题进行研究.以提高结构隔声效果为目标，以复合材料铺层厚度、铺层角度等参数为设计变量，开展复合材料结构隔声优化.

1 声传输理论

板结构嵌在无限障板上，将整个空间分为2个声场：声入射场（z＞0）和声辐射场（z＜0）.设入射平面声波为谐波，入射波斜入射到结构上表面，其入射角为φ，方位角为θ.在板结构入射面上，由入射波引起的板结构振动，该振动由结构介质传到声辐射面，最后在声辐射场形成结构声辐射.结构声传输模型见图1.

1.1 入射平面声波

如图1，以入射角度（φ，θ）的平面声波方程为

式中：ω为声波圆频率；P为入射波幅值；kx，ky和kz分别为入射声波波数在x，y和z方向上的分量，并满足：kx＝k0sinφcosθ，ky＝k0sinφsinθ，kz＝k0cosφ.其中：k0＝ω／c为声波在入射区波数；c为声波在入射区的声速.

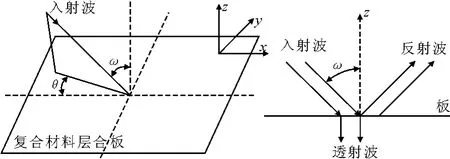
图1 声传递模型

1.2 结构动力响应

在入射波激励下，考虑流体加载作用下的结构运动方程为：

式中：Z＝（－ω2M＋iωC＋K）／iω 为 结构阻抗矩阵；M＝Mf＋MS为质量矩阵，MS为结构质量矩阵，Mf为附加质量矩阵；K为结构刚度矩阵；C为结构黏性阻尼矩阵；｛v｝为结构振动速度向量；G为方向余弦转矩阵；A为结构形状矩阵，并有A＝，N为形状函数矩阵；｛p｝为结构表面节点入射声压向量.结构表面法向速度向量｛vn｝满足：｛vn｝＝GT｛v｝.

1.3 声辐射方程

由Rayleigh积分可计算激励力作用下位于无限障板上的板结构板一侧半无限域流体介质中场点P（位置向量为r）产生的辐射声压p（r，ω）：

式中：ρ为声辐射场域的流体密度；S为结构声辐射表面面积；R＝｜Q－P｜，Q为结构表面S上任意点.结构辐射场域声功率为：∏＊＝.其中：A为半无限域内流体介质中与无限障板平面相接的半球球面.

2 传声损失优化方程

2.1 传声损失方程

在结构声传输研究中，用传声损失来描述结构的隔声性能.传声损失可分为声压级和声功率级，从能量观点用声功率级表示比较直观.在声场中，以角度（φ，θ）入射的平面声波的入射波声功率为

式中：a，b分别为复合材料板的长度和宽度.对于平面声波在空气中以角度（φ，θ）入射到板面传播到板面另一侧半无限域流体介质中的传声计算模型，建立复合材料层合板结构的传声损失为

式中：WI为入射声功率；W＊为辐射声功率.

2.2 传声损失优化模型

由传声损失公式可建立传声损失优化方程，实现结构隔声要求.结构声传输优化就是在设计空间内搜索一组设计变量，使结构在确定的表面入射平面声波条件下，使得结构另一侧表面的结构－声辐射功率最小，即传声损失值STL（x）最大.结构传声损失优化问题可写成

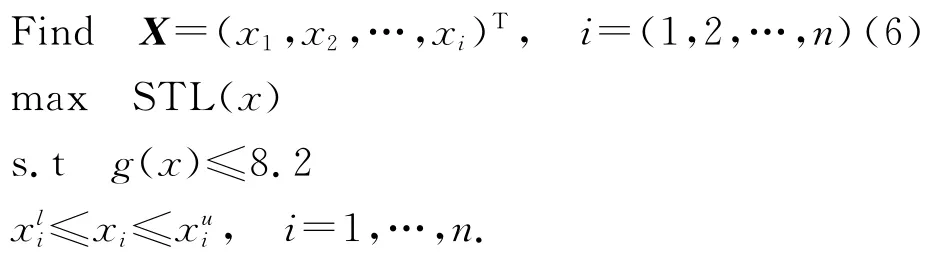
式中：设计变量包括铺层厚度、铺层角度等参数，其上下限约束分别为，g（x）结构质量.复合材料优化是通过改变铺层厚度和铺层角度等设计变量，满足给定的设计要求.

3 数值算例

3.1 计算模型

以四边简支复合材料层合板结构为例，进行复合材料层合板的结构声传输优化.矩形板结构尺寸为：1 200mm×800mm，见图2.在数值计算中，用有限元法进行结构动力响应分析，有限元单元为基于一阶剪切理论－Mindlin理论的四边形四节点单元.板结构离散为425个节点和384个单元.

图2 复合材料模型

在结构初始设计中，复合材料共铺9层，每层铺层厚度均为0.5mm，分别定义为：ti（i＝1，2，…，9）.复合材料铺层方向是对称，各初始铺层角度为：（0°／45°／90°／－45°／0°／－45°／90°／45°／0°），分别定义为：θj（j＝1，2，…，9）.

复合材料力学参数：E11＝34.5GPa，E22＝18.5GPa，G12＝ G13＝4.36GPa，G23＝3.75 GPa；ρ＝1 900kg／m3.

在声学计算中，空气密度ρ＝1.225kg／m3；声速c＝343m／s；声功率参考值：W0＝1×10－12W.

在声传输计算中，为减少计算量，将平面入射声波的入射角简化为：φ＝45°，θ＝0°.计算表明，在入射声波作用下，在33Hz和123Hz处出现比较大的声辐射功率值，在33Hz处有最大值129.9 dB.

定义复合材料铺层厚度设计变量约束条件为：0.000 2m≤ti≤0.001m，i＝1，2，…，9，并定义为离 散 型 形 式：（0.000 2／0.000 3／0.000 4／0.000 5／0.000 6／0.000 7／0.000 8／0.000 9／0.001）.定义复合材料铺层角度设计变量约束条件为：－90°≤θi≤90°，i＝1，2，…，9，并定义为离散型形式 （－60°／－45°／－30°／0°／30°／45°／60°／90°）.

对文中所涉及的复合材料离散变量优化问题，采用遗传算法进行优化.遗传算法具有极强的“鲁棒性”和良好的全局最优解搜索能力，可用于连续变量亦可用于整数型或离散型变量.

文中，先分别对铺层厚度和铺层角度进行优化，然后同时进行铺层角度和铺层厚度的集成优化.

3.2 铺层厚度优化

铺层厚度优化是优化各个铺层的厚度，在满足约束条件下使整个结构传声损失最大.在复合材料结构的铺层厚度优化中，需考虑材料铺层厚度的对称性.通过进行铺层厚度优化，结构的总重量为8.2kg，满足优化的约束条件.优化后各铺层厚度分别为：（0.000 8／0.000 5／0.000 3／0.000 3／0.000 7／0.000 3／0.000 3／0.000 5／0.000 8m）.

图3所示为铺层厚度优化前后的结构传声损失，在最大辐射功率值处其最大结构传声损失值增加了约9.4dB.

图3 铺层厚度传声损失优化

图4所示为结构铺层厚优化前后的结构－声辐射功率，其最大辐射功率值减少了约9.4dB.

图4 铺层厚度声辐射优化

3.3 铺层角度优化

复合材料结构铺设角优化的目的是搜索一组铺层角度向量θ＝［θ1，θ2，…，θ9］，使得整个结构传声损失最大.在铺层角度优化中，考虑材料铺层角度的对称性.通过铺层角度优化，总重量为8.2kg，满足优化约束条件.优化后复合材料铺层角度分别为：（0°／45°／60°／－45°／0°／－45°／60°／45°／0°）.

图5所示为结构铺层厚度优化前后的结构传声损失，在最大辐射功率值处其最大结构传声损失值增加了11dB.

图5 铺层角度传声损失优化

图6所示为结构铺层厚优化前后的结构－声辐射功率，其最大辐射功率值减少了约11dB.

图6 铺层角度声辐射优化

由图3和图5可知，在最大声辐射功率处，通过铺层厚度优化，其结构传声损失值增加了9.4 dB；而通过铺层角度优化，结构传声损失值增加了11dB.说明复合材料层合板铺层角度和铺层角度的结构传声损失优化的效果比较明显，这与材料各向异性程度有关.

3.4 铺层厚度和铺层角度集成优化

在这种优化计算中，将同时进行复合材料铺层厚度优化和铺层角度优化的集成优化，即铺设角和铺层厚度交替收敛到优化解.通过同时进行铺层角度和铺层厚度的优化，总重量为8.02kg，满足优化的约束条件.结构优化后，复合材料的各个铺层厚度分别为：（0.000 7／0.000 4／0.000 3／0.000 5／0.000 6／0.000 5／0.000 3／0.000 4／0.000 7m）；复合材料的各铺层角度分别为：（0°／－60°／30°／45°／0°／45°／30°／－60°／0°）.

图7所示为结构铺层厚优化前后的结构传声损失，在最大辐射功率值处的最大结构传声损失值增加了21dB.

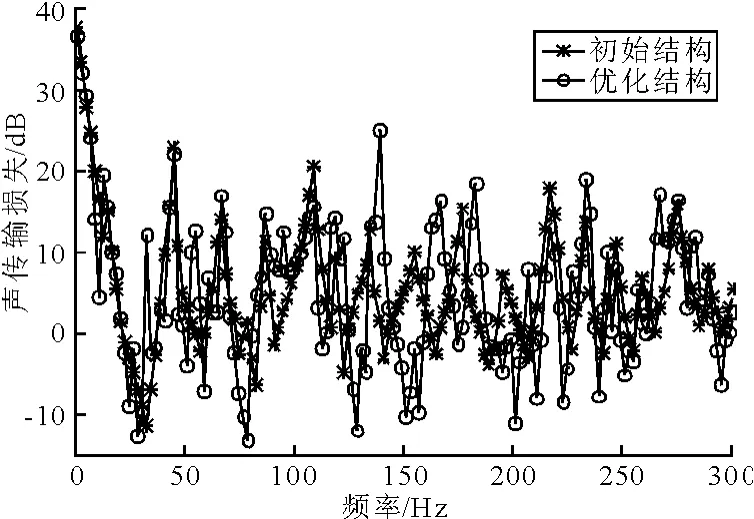
图7 铺层集成优化传声损失

图8所示为结构铺层厚优化前后的结构－声辐射功率，其最大辐射功率值减少了约19dB.

图8 铺层集成优化声辐射

由图7和图8可知，通过同时对铺层厚度和铺层角度的集成优化，其优化效果比单独采用铺层角度优化或铺层角度优化更为明显.

4 结束语

开展复合材料板传声特性数值优化分析，计算表明：进行复合材料层合板的铺层角度和铺层厚度等参数优化，可改善结构隔声特性；对于复合材料的各向异性特性，铺层角度对隔声特性产生较大影响.

［1］王旌生，吴有生.粘弹性复合材料结构水中振动及声辐射研究进展综述［J］.船舶力学，2007，11（5）：804－811.

［2］陈美霞，杜 磊，陈乐佳，等.基于边界元法的平板结构声振性能数值计算［J］.武汉理工大学学报：交通科学与工程版，2009，33（6）：1048－1051.

［3］李海涛，朱 锡，王 林，等.水下均匀复合层结构的声特性研究［J］.武汉理工大学学报，2008，30（6）：105－109.

［4］黎 胜，赵德有.复合材料层合板的铺层几何对结构声传输的影响［J］.振动与冲击，2001，20（2）：86－88.

［5］洪 明，王 晴.基于Zig－Zag模型夹层板振动与声传输特性数值模拟研究［J］.船舶力学，2010，14（8）：938－944.

［6］达内什柔，努里，泰尔毕图第.考虑横向剪切变形时通过层合复合材料圆柱壳的声音传输分析模型［J］.应用数学和力学，2008，29（9）：1057－1068.

［7］LEE C M，XU Y.A modified transfer matrix method for prediction of transmission loss of multilayer acoustic materials［J］.Journal of Sound and Vibration，2009，326（1－2）：290－301.

［8］LEGAULT J，ATALLA N.Numerical and experimental investigation of the effect of structural links on the sound transmission of a lightweight double panel structure［J］.Journal of Sound and Vibration，2009，324（3－5）：712－732.

［9］WANG S C，DENG Z X，SHEN W D.Sound transmission loss characteristics of unbounded orthotropic sandwich panels in bending vibration considering transverse shear deformation［J］.Composite Structures，2010，92（12）：2885－2889.

［10］XIN F X，LU T J.Analytical modeling of fluid loaded orthogonally rib－stiffened sandwich structures：Sound transmission［J］.Journal of the Mechanics and Physics of Solids，2010，58（9）：1374－1396.

［11］李 烁，徐元铭，张 俊.基于神经网络响应面的复合材料结构优化设计［J］.复合材料学报，2005，22（5）：134－140.

［12］LEE D S，MORILLO C，BUGEDA G，et al.Multilayered composite structure design optimization using distributed／parallel multi－objective evolutionary algorithms［J］.Composite Structures，2012，94（3）：1087－1096.

［13］XU Z S，HUANG Q B，ZHAO Z G.Topology optimization of composite material plate with respect to sound radiation［J］.Engineering Analysis with Boundary Elements，2011，35（1）：61－67.

［14］DENLI H，SUN J Q.Structural－acoustic optimization of sandwich cylindrical shells for minimum interior sound transmission［J］.Journal of Sound and Vibration，2008，316（1－5）：32－49.