有关固体材料箱型结构的弯矩方程有限元分析

金 鑫 付 会

(吉林省城乡规划设计研究院，长春 130061)

1 CHBDC的固体材料箱型结构的方程式

1.1 方程式

Duncan等人[1](1985)颁发的因素冠和后弯曲弯矩方程，称为Mcf和Mhf，诱发因素考虑固体材料的相互作用，既有尺寸限制，如表1所示的铝框结构在3个施工阶段的恒载和活载;回填土的覆盖和活载公式(1)和(2).

式中，Mcf为初始弯矩;Mhf为后弯曲弯矩;αD为恒荷系数(=1.25);αL为活荷系数(=1.75);DLA为动态活荷差(DLA=－0.15 H+0.4)，当跨度不少于2 m时.此外，McD和MhD属于一个结构静态，McL和MhL由于活荷导致，具体推导过程相见公式(3)～(11).

式中，κ为初始弯矩系数(=0.70 －0.0328 Dh);kR为折减系数(=0.425 H+0.48≤1.0);γ为固体单位重量;LL活荷作用在固体材料上的长度;k1，k2，k3为3个施工阶段细数，详见图1，公式(9)～(11).k1γDh3详见公式(7)是由于回填土产生的弯曲弯矩.k2γ(H－0.30)Dh2详见公式(7)是回填和覆盖深度之间缠身的弯矩.公式(8)是由于活载分别产生的弯矩.

2.2 讨论

弯矩方程在固体材料箱型结构中有两个限制.第一，虽然最近有大跨度381 mm×140 mm的波纹板，但弯矩公式普遍使用在普通博文铝板上.换言之，采用深波纹板的弯矩方程的系数应增加.增加的部分如图2所示.结果表明，跨度较长和保护层厚度较高，根据相同的配置和保护层厚度，即增加的比率，与铝框结构比较的刚度增加;第二，弯矩方程的限值是2.7 m～8.0 m.对于大于8.0 m的结构需要进行评估.跨度在2.7 m～12.0 m弯矩系数趋势见图3.因此，它产生负弯矩是不合逻辑的，因为有来自正强度产生的正弯矩.

图1 材料结构的三个施工阶段

图2 土体材料结构与铝框结构弯矩的比值

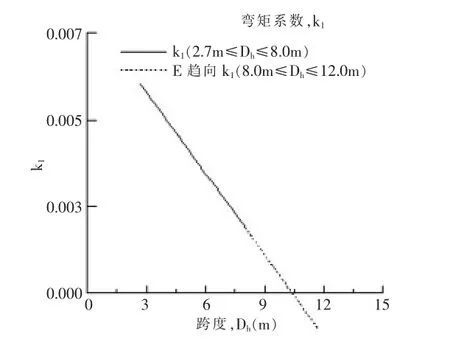
图3 弯矩方程的系数k1

3 对2000年CHBDC弯矩方程系数的分析

3.1 恒载系数k1，k2的分析

恒载弯矩方程如下:

图4代表系数，k1是通过k1γDh3诱导并利用y轴与横坐标(8个跨度)产生结果与CHBDC作的比较[2].它表示CHBDC的弯矩系数k1在超过10.5m跨度时小于分析数值.这说明产生负的弯矩是不符合逻辑的.本文研究提出的系数k1，用最小平方乘法计算的各种跨度弯矩如下:

图5代表系数k2是通过k2γDh2诱导相同斜率8个跨度并与CHBDC作比较.虽然k2是一个常数=0.053，随着跨度增加，系数k2随之减小.因此，本研究提出的方程系数k2通过各种跨度的结果分析如下:

图6表示3 m和12.315 m各种跨度有限元分析的弯矩MD与CHBDC的比较.

图4 弯矩系数k1

图5 弯矩k2

图6 由横荷、跨度、覆盖深度引起的弯矩

3.2 由活荷作用对系数k3的分析

活荷引起的弯矩公式(15).

LL为HS－20的等效线荷[3];Dh为结构的跨度;系数k3是由(11－a)和(11－b)计算而来的.本文研究提出的系数k3通过以下两种方法:系数k3分析1

通过H/Dh假设一个常数0.2和系数k3，公式(16).

a，b通过下面的方法计算.两边都除以LLDh(H/Dh)0.2并把公式(16)带入公式(15)，k3的aDh+b在图7中通过标准跨度除以6 m的最小平方法表示出来.在图7中，虚线由aDh+b在CHBDC公式中诱导，实线则在本文中表达出来.随着跨度的增加，当跨度超过6 m时，有限元分析数据下降.但在没有有限元分析中没有这种趋势.因此，本研究提出的方程如下:

系数k3分析2

k3为跨度的函数;Dh和k3的分母是以跨度的一个比率函数H/Dh.在这里假设函数k3见公式(18).

a，b，α是有以下过程计算出来的.两边都除以LLDh利用log把公式(18)代入公式(15)得出公式(19).图8指出α在3 m和12 m之间不同跨度与CHBDC的比较.k3和aDh+b详见图9.

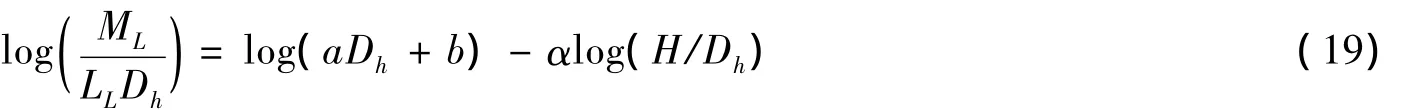
图7 aDh+b的跨度

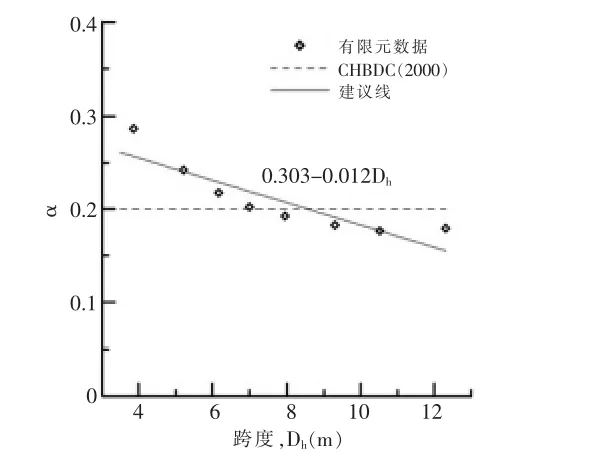
图8 α不同跨度

图9 aDh+b不同跨度

α =0.303 － 0.012 Dh

通过比较系数k3

图10比较系数k3通过有限元分析计算对比CHBDC和公式(1)，(2)，但比较结果误差小于10%.

图11表明在相同条件下不同跨度和覆盖深度的弯矩ML.ML由公式(1)和(2)计算，并与有限元的数据一致.然而，当跨度大于8 m时，误差可能超过一倍以上，公式(1)，(2)的弯矩与有限元数据误差小于5%.

3.3 初始弯矩系数k的分析

当结构设计时，初始和末始在弹性时破坏.但是，设计的弯矩是上述弯矩的总和.因此，应除以系数κ.初始弯矩系数κ表示跨度的一个函数.Dh由公式(21)表达.

虚线α和aDh+b是由CHBDC的公式推导出来.虽然α是常数=0.2，但在CHBDC公式中随着跨度增加，在图8中它本身减少，但尽管aDh+b在CHBDC中是第一个多项式函数，但在图9中表示为一个常数.基于这些结果，系数k3由一个恒定的分子和分母组成，通过计算各种跨度和高度作为第一多项式函数如下:

图12表示初始弯矩系数κ，由跨度和保护层厚度的有限元分析的结果所计算.虚线是由公式(21)计算而得.

图10 跨度和覆盖深度的弯矩系数k3

图11 由于活荷产生的弯矩

图12 初始弯矩系数κ

4 结论

本文分析了这种结构的玩具方程系数的影响.弯矩方程的系数k1，k2，k3和κ是有限元分析的结果且低于保守的条件.尤其，系数k3是由于活荷作用产生弯矩的总和.提出的与有限元分析的方程计算结果比较表明差异小于5%.虽然2000年在加拿大修建的CHBDC采用这种结构一直限制在3 m～8 m，并没有太多的改良，但使用新的参数方程计算可以计算到12 m跨度.

[1]Duncan，J.M.，Seed，R.B.Design of Corrugated Metal Box Culverts[S].Washington，DC.1985.

[2]Canadian Standards Association.Canadian Highway Bridge Design Code[S].Ministry of Transportation of Canada，2000.

[3]Dong－Ho Choi，Gi－Nam Kim.Evaluation of moment equation in the 2000 Canadian highway bridge design code for soil－metal arch structures[J].Canadian Journal of Civil Engineering，2004，31(2):281 －291.