铝合金板带热连轧轧件温度场的有限元模拟

王卫卫，易幼平，谢满堂

（1.中南大学机电工程学院，长沙410083；2.一重集团大连设计研究院有限公司，大连116600）

0 引 言

轧件温度是铝合金板带热连轧工艺的一个重要参数，其分布及均匀性直接影响产品的尺寸精度、微观组织、力学性能以及轧机负荷的合理分配。因此对轧制过程中轧件温度计算及控制一直是热连轧研究的重要方向之一。目前常用的轧件温度预测手段有解析法、有限差分法和有限元法。国外多采用有限差分法或有限元法建模，则结合人工智能模型对轧制过程中轧件温度进行预测［1－4］。国内铝合金板带热连轧生产线多由国外引进，轧件温度计算等基础研究仍以传统的解析法建模为主，并对实际轧制条件进行了大量简化，使得各道次温度计算精度较低，尤其在变品种、变工艺轧制时误差较大，因此迫切需要采用新的方法来提高计算精度［5－6］。为此，作者利用MARC软件结合某铝厂典型产品5xxx系铝合金板带热连轧工艺规程对轧制过程中轧件温度场进行模拟计算，分析了轧制过程中轧件温度变化及分布规律，并利用现场实测数据对模型计算结果进行了验证，为铝合金板带热连轧工艺制定提供参考。

1 有限元分析模型的建立

1.1 热连轧工艺参数

热连轧开始时，首先将加热到初始温度490℃的轧件坯料通过辊道输送到轧机左侧入口。第一道次轧件由左侧轧入，右侧轧出；第二道次则由右侧轧入，左侧轧出；如此类推进行15道次往复热连轧，具体工艺规程如表1所示。轧辊材质为38Cr2Mo2MnVSi钢，半径为465mm。

表1 5xxx系铝合金板带热连轧工艺参数Tab.1 The rolling process of 5xxx series aluminum plate

1.2 几何模型

根据文献［7］，扁平板热轧时，轧件温度梯度主要沿厚度方向和轧制方向，宽度方向温度梯度很小。因此，忽略轧件宽度方向的温度变化，建立二维有限元分析模型。因为轧辊刚度较大，故将轧辊设为传热刚体，轧件设为弹塑性体。模拟时为了保证轧件的顺利咬入，在轧件尾部设一绝热刚性推板，以轧辊线速度运动推动轧件前进，咬入后推板自动撤离。为了真实地反映出铝合金板带热连轧过程中轧件温度场的变化以及保证计算结果的精度，同时尽量缩短模拟计算时间以及提高收敛性，将轧件划分为均匀细密的网格，并采用11号有限刚度平面应变全积分单元描述；轧辊与轧件接触的外圆周部位网格密度与轧件网格密度保持一致，然后其网格密度从外圆向圆心逐渐减小，形成外密内疏的网格，并采用39号无限刚度全积分单元描述。建立的二维有限元分析模型如图1所示，x轴为轧制方向，y轴为轧辊压下方向；另外，需要说明的是实际用于计算分析的网格密度远比示意图中的大，从而保证计算精度。

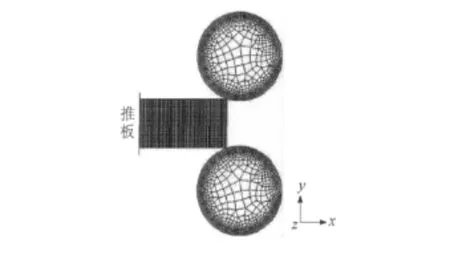
图1 二维有限元轧制模型Fig.1 The two－dimension computer model of rolling

1.3 边界条件

1.3.1 辐射传热

在铝合金板带热连轧过程中，轧件上下表面和四个侧面与环境存在热辐射换热，因为轧制时间较长，散热量较大，所以建模时必须考虑热辐射对轧件温度变化的影响。辐射传热系数hr计算公式为［8］

式中：ε为黑度，取0.2；σ 为波尔兹曼常数，取5.67×10－8W·m－2·K－4；Tw为轧件温度，K；Tf为空气温度，K。

计算得到轧制时轧件的辐射传热系数为7.04W·m－2·K－1。

1.3.2 对流传热

当轧件在辊道和轧机上运动时，其自由表面和周围空气存在对流换热。根据文献［9］，热连轧时因周围空气与轧件温度相差较大，两者间对流换热属于混合对流传热，由自然对流传热和强迫对流传热共同决定，混合对流传热系数h由下式得到：

式中：NuM为混合对流时的努塞尔数；λm为空气的热传导系数，W·m－1·K－1；l为轧件长度，m。

计算得到轧制时轧件的混合对流传热系数为9.41W·m－2·K－1。

1.3.3 摩擦生热

轧制过程压下量较大，此时轧件与轧辊间的摩擦不满足库伦摩擦模型，因此采用修正剪切摩擦模型描述［10］，该模型认为摩擦应力τf是材料等效切应力的一部分，此时摩擦热Qf的计算公式为

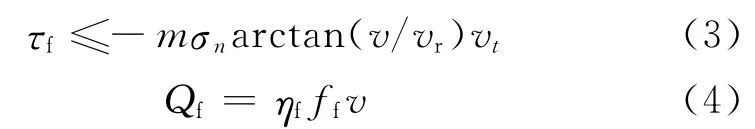
式中：τf为剪切摩擦应力，MPa；m为轧件与轧辊间的摩擦因数，取0.3；σn为法向应力，MPa；v为轧板与轧辊的相对滑动速度，m·s－1；vr为发生滑动时接触体之间的临界相对滑动速度，m·s－1；vt为相对滑动速度方向上的切向单位向量，vt＝v｜v｜－1；ηf为摩擦热转变效率，取1；ff为剪切摩擦力，N。

1.3.4 塑性变形热

轧制过程中，塑性变形热主要产生在变形区，设变形抗力为恒定值，并认为其近似等于轧辊作用在轧件上的平均压力，那么可以用下式计算轧制过程中的塑性变形热Qp。

式中：d1，d2分别为轧制前后轧件的厚度，m；k为变形抗力，MPa；pm为轧辊作用在轧件上的平均压力，MPa；ηp为转化为热能的塑性变形功占总塑性变形功的比例，取0.9［11］。

1.3.5 接触传热

轧件与轧辊间接触传热受表面形貌、介质材料、热流方向、润滑条件等因素影响，目前还处于研究阶段，尚没有统一的理论公式。根据文献［4，12］，铝合金板带热连轧过程中轧件与轧辊间接触换热系数hc可以由下式得到

式中：p＊＝，为无量纲接触压力；p为轧件与轧辊间的接触压力，MPa；H 为接触副间较软材料的显微硬度，MPa。

1.4 热物性参数

在铝合金板带热连轧过程中，选择精确的轧件材料热物性参数是提高计算精度的关键。为此，作者以5xxx系铝合金工业铸锭为试验材料分别进行了DSC试验和热脉冲法试验，获得了其随温度变化的比热容和热传导系数，如图2所示。

1.5 热压缩本构模型

热压缩本构方程是铝合金板带热连轧过程有限元模拟重要的材料模型，MARC软件材料库中缺少所研究铝合金的相关数据。为此，作者在Gleeble－1500型热模拟试验机上进行了5xxx系铝合金热压缩试验。图3为该铝合金在不同变形温度及变形速率下的真应力－真应变曲线。采用周纪华铝合金变形抗力模型对热压缩试验获得的真应力－真应变曲线进行非线性回归拟合。

由热压缩试验可知5xxx系铝合金在基准变形条件下的变形抗力为180.73MPa，回归拟合得到其热压缩本构模型如下所示［13］：

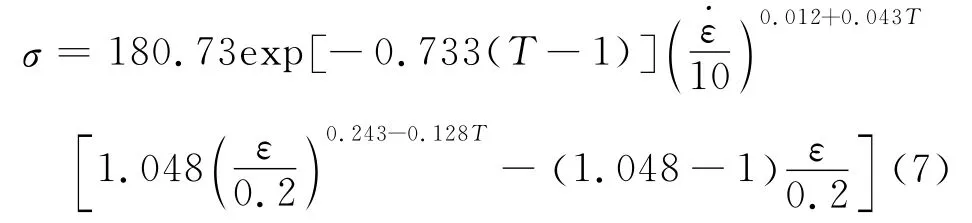
2 模拟结果讨论

2.1 轧件温度场的有限元模拟

利用上述建立的有限元模型、边界条件及得到的热物性参数按照轧制规程对5xxx系铝合金热连轧共15个道次开展了轧件温度场有限元模拟。取轧件中段某一截面从上表面到中心各节点的瞬时温度值，如图4所示。可以看出，轧件表面温度变化梯度最大，中心温度变化梯度最为平缓，随轧制的进行，表面温度和中心温度分别呈先下降后上升和先上升后下降的变化规律。这是因为前9个道次轧件较厚，轧件在厚度方向上热传导较小，表面温度主要受接触传热影响而下降，中心温度主要受塑性变形热影响而上升，因此表面温度和中心温度间的差值越来越大；随着轧件厚度变薄，轧件表面和中心的热传导作用慢慢变强，使得表面温度上升而中心温度下降，轧件温度场趋向于一致。第11道次轧件需切除头部、尾部废料并进行测温，在辊道上经过较长时间的对流辐射传热，此时轧件厚度方向温度基本一致（温度梯度小于1℃）。因此，实际生产中可以在此时检测表面温度，并将其视为轧件的平均温度。

图4 轧件厚度方向不同位置温度的变化曲线Fig.4 Variation curves of temperature for positions along thickness direction on the workpiece

将轧件厚度方向上所有节点温度的平均值作为轧件的平均温度。由图5可以看出，热连轧过程中轧件平均温度呈先上升后下降的变化规律，这是由轧制过程中塑性变形热造成的温升和接触传热、对流辐射散热造成的温降共同决定的。由表2不同边界条件对铝合金板带平均温度的影响可以看出，塑性变形温升和接触换热温降对轧件温度场影响显著，且两者均随着轧制压下率增大而增大；对流辐射散热对轧件温度场影响相对较小，在轧制初期几乎可以忽略，只有在轧件较薄且空冷时间较长的道次，才对轧件平均温度产生明显的温降。

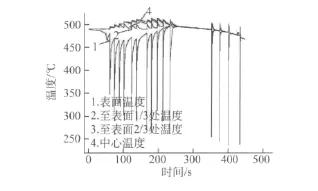
图5 轧件平均温度的变化曲线Fig.5 Variation curve of average temperature for workpiece

表2 不同边界条件对平均温度的影响Tab.2 The effects of different borderline conditions on average temperature

2.2 有限元模拟结果的试验验证

为了检验有限元计算结果的可靠性，将模拟得到的轧件表面温度与现场红外检测的轧件表面温度进行对比，如表3所示，可知两者最大温差为9.4℃，最小温差为2.3℃，平均温差为5.2℃，平均误差为1.1%，两者吻合较好，表明基于 MARC软件建立的有限元模型是可靠的。

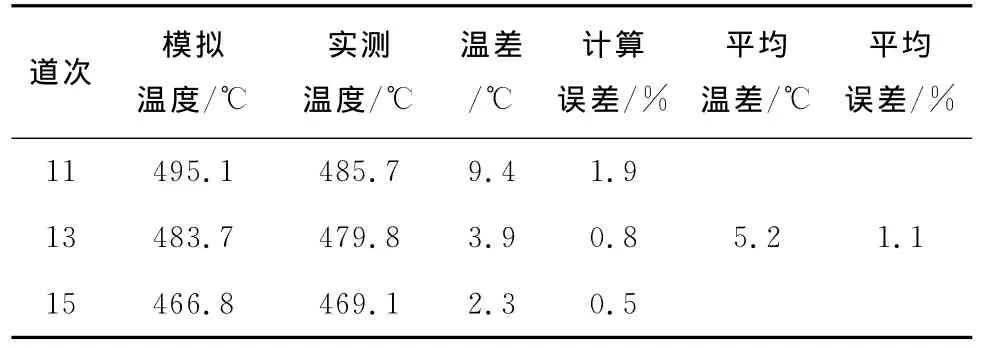
表3 模拟温度与实测温度的误差Tab.3 Error of temperature between simulation and actual measurement

3 结 论

（1）通过试验获得了5xxx系铝合金热物性参数，建立了热压缩本构模型和热连轧过程轧件二维温度场有限元计算模型，有限元计算结果与实测温度平均误差为1.1%，两者吻合较好。

（2）在热连轧过程中，轧件表面温度变化梯度最大，越靠近中心变化梯度越小，表面温度随轧制的进行呈现先下降后上升的变化规律，中心温度和平均温度呈现先上升后下降的变化规律，在11道次结束后，轧件厚度方向上温度基本一致，温度梯度小于1℃。

（3）塑性变形热和接触热传导对轧件温度场影响显著，对流辐射散热影响较小，三者共同作用决定了轧件各点温度变化规律。

［1］李海军.热轧带钢精轧过程控制系统与模型的研究［D］.沈阳：东北大学，2008.

［2］肖根福.精轧温度过程控制模型研究［D］.南昌：南昌大学，2005.

［3］肖云平，刘义伦，何玉辉.铝热连轧温度场模拟在 Marc中的实现［J］.重庆工程学院学报：自然科学版，2009，23（10）：36－41.

［4］何玉辉.板带多道次热轧过程温度场数值模拟与温降模型研究［D］.长沙：中南大学，2010.

［5］李立新，汪凌云，周家林，等.中板精轧阶段温度场的有限元分析［J］.武汉科技大学学报：自然科学版，2002，25（2）：124－125.

［6］孙登月，杜凤山，杨喜荣，等.2050轧机粗轧过程温度仿真模型的研究［J］.钢铁研究学报，2004，16（2）：33－36.

［7］张鹏，鹿守理，高永生，等.板带轧制过程温度场有限元模拟及影响因素分析（Ⅱ）［J］.北京科技大学学报，1998，20（1）：99－102.

［8］李毅波.连续铸轧多场耦合建模及工艺参数匹配规律的仿真研究［D］.长沙：中南大学，2006.

［9］康煜华，刘义伦，何玉辉.铝合金轧制过程中的热力耦合分析［J］.锻压技术，2008，33（5）：92－94.

［10］康煜华，刘义伦，何玉辉.铝合金单道次热轧过程的温度模拟［J］.机械工程材料，2010，34（4）：92－96.

［11］郭金龙，康煜华，刘义伦，等.铝热连轧粗轧区轧件温度场的数值模拟［J］.湖南科技大学学报：自然科学版，2007，22（2）：31－34.

［12］湛利华.界面接触热阻实验与建模及其在快凝铸轧参数设计中的应用［D］.长沙：中南大学，2001.

［13］周纪华，王再英，高永生，等.铝合金流动应力数学模型［J］.北京科技大学学报，1994，16（4）：351－356.