基于灰色马尔科夫模型的卷烟需求预测

夏正威

(上海第二工业大学理学院,上海201209)

基于灰色马尔科夫模型的卷烟需求预测

夏正威

(上海第二工业大学理学院,上海201209)

随着市场经济的不断发展,卷烟经营和生产都越来越尊重市场、重视需求,要求更加贴近卷烟零售客户和消费者。因此,科学、准确的市场需求预测是卷烟经营工作的核心和基础。运用科学的方法,准确有效地分析卷烟市场的真正需求,预见其发展趋势,能够使经营者掌握市场供求变化的规律,为经营决策提供可靠的依据。针对卷烟需求趋势与波动并存的特点,利用灰色马尔科夫模型,根据状态转移概率来推断卷烟需求的变化趋势,得到预测结果,并对未来的卷烟需求进行准确有效的分析。

灰色马尔科夫模型;状态转移概率;需求预测

0 引言

卷烟销量具有不确定性,其随机波动性较大,是否能找到一种方法能较准确地分析卷烟销量的变化规律,能够对其未来变化趋势进行预测,使经营者掌握市场供求变化的规律,为经营决策提供可靠的依据。本文针对这些问题,建立卷烟销量变化的数学模型,在数据上给予解答。

参考数据为1999～2008年10年间全国GDP和卷烟消费量的实际数据[1],见表1。

表1 1999～2008年全国GDP和卷烟销量统计表Tab.1 Statistics of national GDP and cigarette sales from 1999 to 2008

1 灰色马尔科夫模型

1.1 模型的介绍

马尔科夫模型是用来预测具有等时间间隔(如一年)的时刻点上随机序列的分布状况。它能找出序列变动的规律,以此来推测未来的变动趋势。卷烟的销量变化就是一个等时间间隔的随机过程,因此,我们运用马尔科夫理论,建立了灰色马尔科夫模型,并根据状态转移概率来推断其变化趋势,确定预测区间,得到预测值,较准确地预测卷烟的需求趋势。

1.2 状态的划分

对于状态平稳(等均值等方差)的随机过程,传统的状态划分方法是以若干常数作为状态的上、下界。由于卷烟销量的趋势变化是一个随机的非平稳过程,我们应考虑一个变化的状态划分准则,这个准则应与考虑的预测对象的基本时序变化趋势相一致。对于一个符合马尔科夫过程的非平稳随机序列ˆy(艺),可根据具体情况划分为若干个状态。状态的划分准则采用相对值为宜[2,3],

相对值=(真实值/拟合值)*100%

式中E乞代表第乞种状态。e乞1,e乞2即灰元,分别表示第乞种状态的上下界。

在划分状态时,要根据实际情况的不同,划分不同的区间个数。一般来说,原始数据较少时,划分区间宜少,以便增加各状态间的转移次数,从而更加客观地反映各状态间的转移规律;原始数据较多时,区间也不妨划分多一些,以便从资料中挖掘更多的信息,提高预测精度。

1.3 构造状态转移矩阵

设数据由状态E乞经过k步变为状态Ej的次数记为,状态E乞出现的次数记为N乞,则由状态E乞经过k步变为状态Ej的转移概率为

根据此概率公式构造状态转移概率矩阵

状态转移概率矩阵P(k)反映了系统各状态之问的转移规律。通过观察P(k)可以预测未来的状态转向。确定了转移概率矩阵P(k)和初始状态E乞后,马尔科夫链就可以确定[4]。

1.4 编制状态预测表

选取距离预测年份最近的m个年份(m为状态的个数),按离预测年份的远近,转移步数分别定为1, 2,···,m。在转移步数所对应的转移矩阵中,取起始状态所对应的行向量,即为各状态出现的概率,对各概率求和,其最大的转移步数所对应的状态即为系统随机值的预测转向状态。

1.5 计算预测值

确定系统未来的状态转移后,就可确定预测值的相对值变动区间

可以用区间的中位数作为未来时刻预测值的相对值,即最终预测值

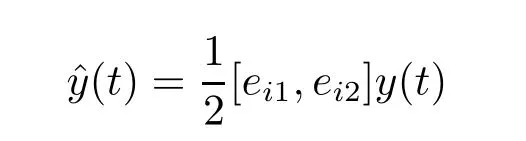
2 模型的应用

2.1 状态划分

根据相对值划分状态标准并结合图1,将卷烟销量划分成4个状态[5-7],见表2。

图1 卷烟销量拟合及预测效果图Fig.1 Fitting and prediction of cigarette sales

表2 卷烟销量拟合及预测效果表Tab.2 Fitting and prediction of cigarette sales

确定各状态的区间划分,见表3。

2.2 构造状态转移概率矩阵

选取距离预测年份最近的4个年份(4为状态的个数),由式(1)和式(2),得出下列状态转移概率

表3 状态区间划分表Tab.3 States interval division

矩阵[5-9]:

(1)步状态转移概率矩阵

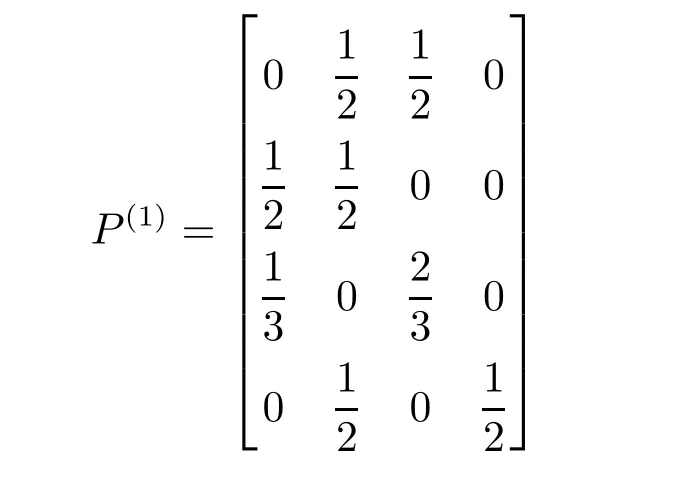
(2)步状态转移概率矩阵

(3)步状态转移概率矩阵

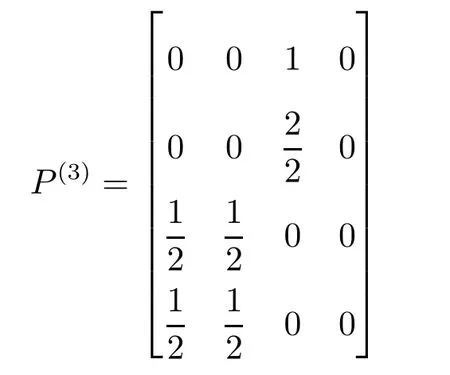
(4)步状态转移概率矩阵

2.3 编制状态预测表

根据以上转移矩阵,编制状态预测表(见表4),在转移步数所对应的转移矩阵中,取起始状态所对应的行向量,组成新的概率矩阵[5-10]。

表4 卷烟销量状态预测表Tab.4 States prediction of cigarette sales

2.4 计算预测值

由表4可知,在状态合计栏中,以状态2的概率最大,因此2009年的全国卷烟销量的相对值在0.96～0.99之间,可以用区间的中点作为系统未来时刻预测值的相对值[11-12],

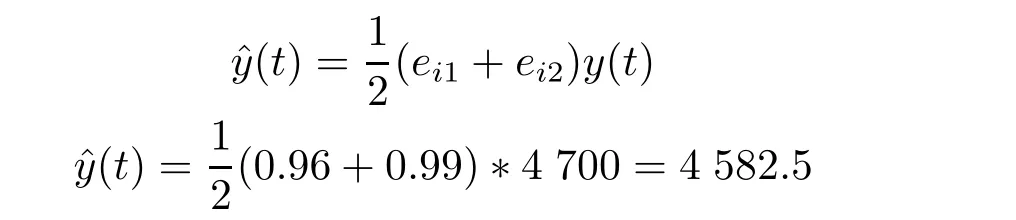
至此可知,2009年的预测值为4 582.5万箱。而2009年全国卷烟的实际销量为4 577.6万箱,由此可知我们的模型预测精度较好。

利用同样的预测方法,我们可以得到2010～2012年的预测值分别为4 662.3,4 872.1,4 990.7万箱,相比较同时期的全国卷烟销量的实际值4 693.2,4 834,4 950万箱,我们的模型预测精度较好。

[1]刘红飞.基于灰色系统理论的广东卷烟消费需求预测研究[J].经济师,2007(1):273-274.

[2]王伟民,汪坛,张国安.基于灰色马尔科夫模型的全国卷烟需求预测研究.中国烟草学报,2009,15(6):66-69.

[3]董泽清.马尔科夫决策规划[M].北京:中国科学院应用教学所,1981.

[4]邓聚龙.灰预测与灰决策(修订版)[M].武汉:华中科技大学出版社,2002.

[5]白远良,吴应禄,程晓苏.我国卷烟需求分析(上)——需求现状与模型构建[J].中国烟草学报,2007,13(3):6-l0.

[6]白远良,吴应禄,程晓苏.我国卷烟需求分析(下)——卷烟需求模型实证分析与结论[J].中国烟草学报,2007,13(4): 55-59.

[7]王森,吴春明.烟草系统卷烟需求预测模型的探讨[J].现代机械,2007(2):4-6.

[8]姜启源,谢金星,叶俊.《数学模型》[M].第三版.北京:高等教育出版社,2003.

[9]甘旭升,端木京顺,田井远.基于灰色马尔柯夫模型的严重飞行事故频数预测[J].空军工程大学学报:自然科学版,2004, 5(1):18-21.

[10]FOX JR W W.An exponential surplus-yield model for optimizing exploited f i sh populations[J].Trans.Am.Fish. Soc.,1970,99(1):80-88.

[11]贺福利,胡勇,陈凉.用灰色马尔科夫链预测模型对我国粮食产量的预测[J].数学的实践与认识,2003(12):45-47.

[12]邵静,王利超,刘新平.灰色马尔科夫模型及其应用.纺织高校基础科学学报,2009,22(3):370-374.

Study on the Prediction of Cigarette Demand Using Grey Markov Model

XIA Zheng-wei
(School of Science,Shanghai Second Polytechnic University,Shanghai 201209,P.R.China)

With the continuous development of market economy,the management and production of cigarettes pay more attention to needs and demands of cigarette customers and consumers.Therefore,scientif i c and accurate prediction for market demand is the core and basis for cigarette management.Using the scientif i c method,a correct and ef f ective analysis for cigarette demand,and foreseeing the trend of its development,comcanies can master the rule of change of the market demand and provide a reliable basis for business decisions.According to the f l uctuating trend of cigarette demand,changes in cigarette demand is infered by the state transition probability based on the grey Markov model and prediction conclusion is gotten.The cigarette demand in the future is analysized accurately and validly.

grey Markov model;state transition probability;prediction of demand

O212.4

A

1001-4543(2013)02-0101-06

2013-03-22;

2013-05-08

夏正威(1980–),男,浙江人,讲师,硕士,主要研究方向为随机过程、动力系统的稳定性,电子邮箱zwxia@sspu.edu.cn。